质量问题的多极子方法

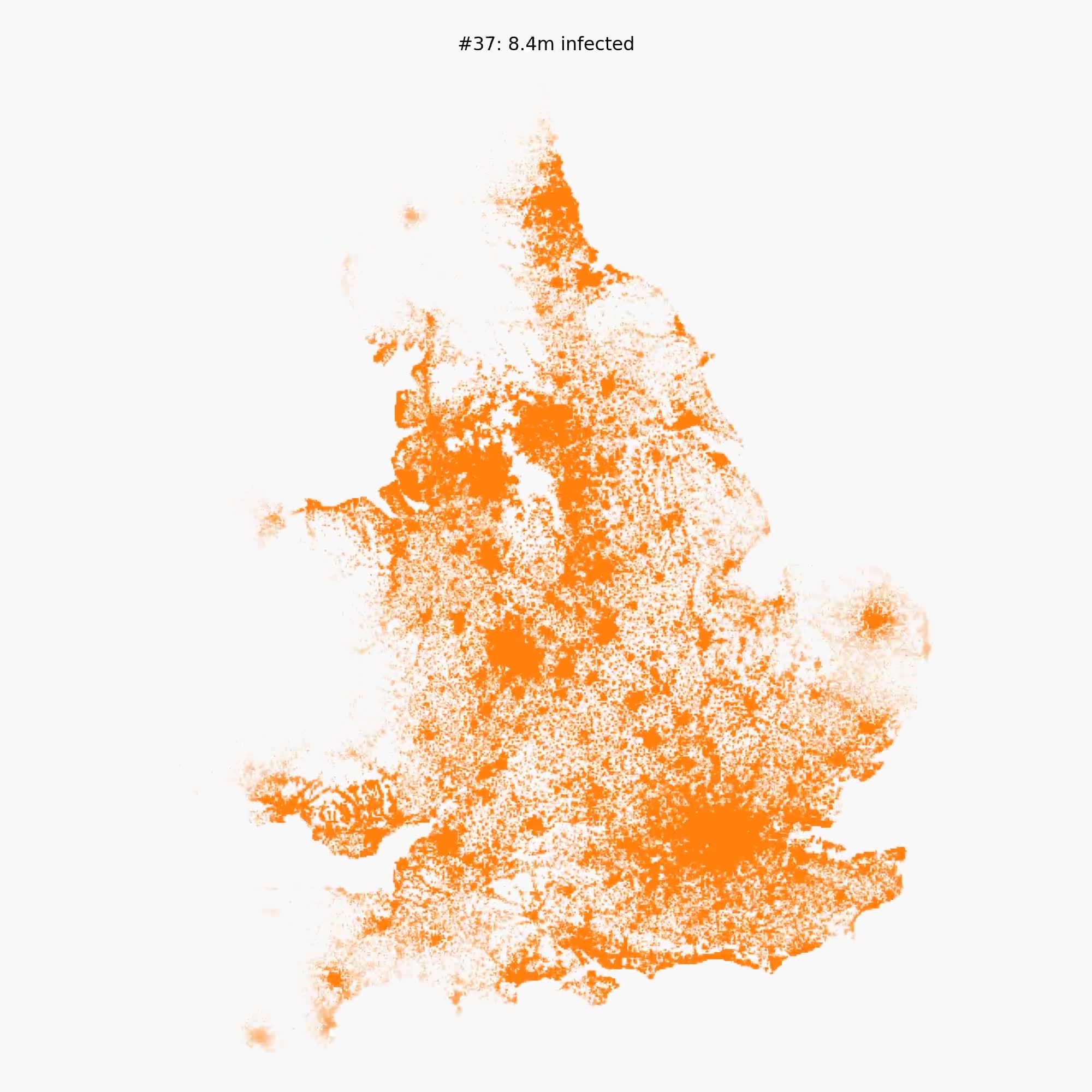
这不是流行病学模式。这是一个流行病学模型的部分技术演示。你现在看到的是英国的1000万模拟人。在这个国家，每个人都有很小的机会感染其他人，而且这种机会随着距离的增加而下降。

有一千万人，你会认为上述动画的每一帧都会涉及到计算100万亿(一千万平方)的互动。即使对于现代的硅来说，这也是很多的！但是，物理学中有一种鲜为人知的算法，它可以在每帧几秒钟内完成这一任务。

该算法--快速多极子方法--在整体上相当复杂。但它有一个关键思想，那就是它的适用性很广，为了它的缘故，我将在不使用任何代数的情况下解释该算法。

技术综述快速多极子方法将二次时间的相互作用问题转化为线性时间问题，最近的一个称为黑盒多极子方法的版本可以对你选择的任何相互作用都能做到这一点。关键思想是近似的层次结构，这也是这篇文章的大部分目的所在。

也许源头是一颗行星，而磁场就是它的引力。也许源是粒子，场是电场。可能源头是感染者，而田野就是传播风险。

对于我们的目的来说，该字段代表的并不是那么重要，因为无论它代表什么，计算它的方法都是相同的。为了计算场，我们依次查看100个等间距的点，并计算每个点的源磁场强度：

如果有多个来源，则它们的字段加在一起。要计算某一点的组合场，需要考虑每个源发出的场。对于100个源和100个点，需要进行100×100=10，000次计算：

不过，这是相当浪费的。如果我们有一堆彼此接近的消息来源，就像我们下面做的那样，那么他们对这一点的贡献几乎是一样的。通过使用近似值，我们可以节省大量工作：将所有震源移动到同一地点，从该地点进行一次计算，然后将计算出的场强乘以该组中的震源数量：

如果我们仔细观察，就会发现这个点并不完全位于场线上。这是因为只有当点远离震源时，我们才能摆脱这种近似。当点离震源很远时，震源可以向左或向右移动一点，不会有太大影响。不过，如果该点离震源很近，那么每个震源的确切位置就很重要了，而这种近似并不能很好地发挥作用：

幸运的是，虽然大多数点与大多数来源相去甚远，所以大多数情况下近似效果都很好。

对于远离一组的所有点，对整个组进行一次计算。

对于靠近组的所有点，对组中的每个源进行一次计算。

这里的“近”和“远”是什么意思？嗯，最糟糕的情况是，如果在被近似的震源旁边的点上使用近似值。为了避免这种最坏的情况，作为一种简单的方法，如果一个群体没有坐在该群体或该群体的邻居之下，我们就会说这一点来自该群体。这就保证了赢得的分数不会恰好接近近似值。

总共进行了3，500次计算-改进了65%！这不是一件小事--但是我们能做得更好吗？

嗯，上面的团队规模完全是随意的。它们没有理由不能大一倍：

总共进行了三千二百次计算。总体而言，这要好一些，但如果我们既可以从上一个例子中获得少量的近距离计算，又可以从这个例子中获得少量的远距离计算，情况会怎样呢？

大比例尺和小比例尺同时使用怎么样？现在的计划看起来是这样的：

在大组比例中的任何远处的点上使用大组近似。

对小组比例中距离较远的任何剩余点使用小组近似。

我们基本上正在改变“近距离”和“远距离”的概念，这取决于我们关注的是大团体还是小团体。逻辑是，对大群体的近似计算可能会使源移动很远，所以近似只会在很远的距离上是准确的。越小的组移动的震源越少，所以近似在更小的距离上就会很精确。

这确实会让我们的计算减少到2500次，但我们没有理由不再重复这个大群体的把戏几次：

这是快速多极子方法的关键思想：我们应该建立一个近似层次，而不是使用只能在一个尺度上使用的一个近似。可以使用较小的近似值来代替要求较高的短程计算。