时间序列建模和预测综合教程

在上一篇文章中，我们已经了解了如何可视化时间序列数据。在这篇文章中，我们将讨论如何使用ARMA和ARIMA模型进行时间序列建模。这里AR代表自回归，MA代表移动平均。

在我们开始讨论ARIMA模型之前，我们应该了解时间序列的平稳性。

如果观测值的均值、方差和协方差在一段时间内没有变化，则称时间序列为平稳序列。

换言之，如果观测值的联合分布不变，并且当时间起点偏移k个量时保持不变，则称一个过程是平稳的。

这意味着均值和方差是恒定的，不依赖于时间。平稳过程有两种类型：严格平稳过程和弱平稳过程。

ARIMA是自回归综合移动平均模型的缩写，是目前应用最广泛的时间序列预测模型之一。

它还解释了连续时间点之间数据或噪声的增长/下降模式。

将ARIMA应用于具有非平稳性的数据，并采用连续观测的差值来消除非平稳性。有时需要多次连续观测的差异才能得到修正的平稳模型。

这就是它被称为集成模型的原因，因为拟合到修改后的序列的平稳模型必须求和或积分，以提供原始非平稳序列的模型。

我们应该将ARIMA模型拟合到平稳和非季节性的时间序列数据，并遵循上面流程图中描述的过程。

首先，您应该绘制数据图表，以发现隐藏的模式、趋势和其他行为。

要稳定和规格化数据，可以使用Box-Cox变换。这是一种变换通常不服从正态分布的数据的方法。

绘制ACF/PACF以确定ARIMA模型的顺序，即p、d和q值。或者，您也可以使用AICC和BICC来确定p、q、d值。选择AICC和BICC最低的。

验证残差并确保它看起来像白噪声，否则请尝试使用不同p、q和d值的修改后的模型。请记住，白噪声的残差可以进行预测。

我们将使用阿莫里市的月度温度数据集。您可以从此链接下载。

将熊猫作为snssns.set(rc={'；figure.figsize'；：(15，6)})%matplotlib inlinedf=pd.read_csv('；./monthly_temperature_aomori_city.csv'；)df['；DATE'；]=pd.to_DateTime(DF[['；Year'；，'；month'；]].assign(DAY=1))df.drop(['；]，smimport matplotlib.pylot作为pltimport海运)导入pdimport statsmods.api。年'；，'；月'；]，位置=真，轴=1)df['；温度'；]=df['；temperature'；]*(9/5)+32df.set_index('；DATE'；，inplace=True)df.to_csv('；./monthly_temperature_aomori_city_updt.csv'；，索引=真)df.head()。

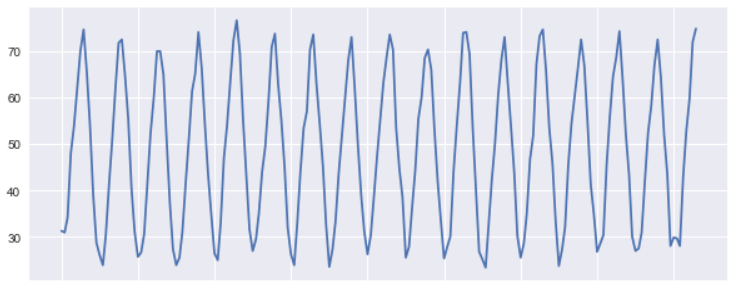
让我们为前200行画一张简单的线条图，以了解数据中的模式以及温度是如何趋势的。看起来这里遵循的是一种循环模式。

我们将绘制前5年的盒子和胡须图，以了解数据分布，并快速获得数据的五点汇总。

如果您正在寻找有关时间序列分析和可视化的深入教程，可以查看此博客，它是此时间序列分析博客的第1部分。

为了进一步分析时间序列数据，分解有助于去除数据的季节性。

基本上，分解有三个组成部分，如下图所示，即趋势、季节性和残差。

您必须选择一种模型类型，也可以是加法或乘法。我们采用了加法模型，因为季节性从开始到结束变化不大。

ARIMA模型对非平稳数据的处理效果更好，我们首先要检查的是数据的平稳性。增广的Dickey-Fuller检验可以用来检验序列是非平稳的零假设。

ADF检验有助于理解Y的变化是否是线性趋势。如果存在线性趋势，但滞后值不能解释Y随时间的变化，则我们的数据将被认为是非平稳的。

从statsmods.tsa.stattools导入adfullerdef check_stantality(TimeSeries)：result=adfuller(timeSeries，autolag='；AIC'；)dfoutput=pd.Series(result[0：4]，index=['；Test Statistics'；，'；p-value'；，'；#LAGS Used'；，'；；##39；，'；]。p-值：%f'；%Result[1])为键打印('；临界值：'；)，结果[4]中的值。Items()：打印('；\t%s：%.3f'；%(键，值))。

检验统计量的值小于5%的临界值，p值也小于0.05，因此我们可以拒绝零假设和时间序列平稳的交替假设似乎是正确的。