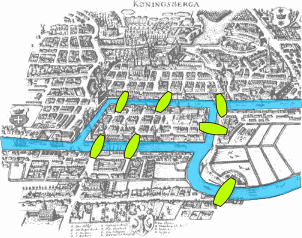
哥尼斯堡的七座桥

跳转到导航跳跃搜索哥尼斯堡的七座桥是一个历史上值得注意的数学问题。它的负解由Leonhard Euler于1736年提出[1]，奠定了图论的基础，预示了拓扑学的思想。[2]。

普鲁士的哥尼斯堡(现在的俄罗斯加里宁格勒)坐落在普雷格尔河的两岸，包括两个大岛-克内夫和洛姆斯岛-这两个岛通过七座桥相互连接，或与城市的两个大陆部分相连。问题是要设计一条穿过这座城市的步道，每座桥都要过一次，而且只有一次。

欧拉证明了这个问题是没有解决方案的。他面临的困难是开发了一种合适的分析技术，以及随后的测试，这些测试以数学上的严谨性确立了这一论断。

首先，欧拉指出，每一块陆地内的路线选择都是无关紧要的。路线的唯一重要特征是跨越的桥梁的顺序。这使得他可以用抽象的术语重新表述问题(为图论奠定基础)，消除除陆地块列表和连接它们的桥梁之外的所有特征。用现代语言来说，人们用抽象的顶点或节点代替每个陆块，用抽象的连接(边)代替每个桥，它只用来记录哪一对顶点(陆块)是由那座桥连接的。由此产生的数学结构称为图形。

因为只有连接信息是相关的，所以图形的图形表示的形状可能以任何方式失真，而不会改变图形本身。只有每对节点之间的边的存在(或不存在)才是重要的。例如，绘制的边是直的还是弯的，或者一个节点位于另一个节点的左侧还是右侧并不重要。

接下来，欧拉观察到(除了在步行的终点)，每当一个人从桥进入一个顶点时，他就会从桥上离开这个顶点。换句话说，在图中的任何漫游过程中，进入非末端顶点的次数等于离开它的次数。现在，如果每座桥都恰好经过了一次，那么对于每一块陆地(除了选择作为起点和终点的那座)，接触该陆地的桥梁的数量必须是偶数(在特定的穿越中，其中一半的桥梁将向陆地横穿，另一半将向远离它的方向横穿)。(#*)。然而，原问题中的四个陆块都被奇数个桥梁触及(一座被5座桥梁触及，另外三座分别被3座触及)。由于一次步行最多只能有两个陆块作为终点，所以步行穿越每一座桥的命题曾经导致了一个矛盾。

在现代语言中，Euler表明，遍历图形的可能性，即恰好遍历每条边一次，取决于节点的度数。节点的阶数是接触它的边数。欧拉的论点表明，所需形式的行走的一个必要条件是图是连通的，并且恰好有零个或两个奇数次的节点。事实证明，这个条件也是充分的--这一结果由欧拉提出，后来被卡尔·希尔霍尔泽证明。这样的步行现在被称为欧拉小路，或以他的名字命名的欧拉散步。此外，如果存在奇数次节点，则任何欧拉路径都将在其中一个节点开始，在另一个节点结束。由于对应于历史Königsberg的图有四个奇数度节点，因此它不可能有欧拉路径。

问题的另一种形式要求提供一条穿越所有网桥并且起点和终点相同的路径。这样的徒步旅行被称为欧拉巡回赛或欧拉之旅。当且仅当该图是连通的，并且根本没有奇数次的节点时，才存在这样的电路。所有欧拉路也是欧拉路，但并非所有欧拉路都是欧拉路。

欧拉的工作于1735年8月26日提交给圣彼得堡学院，并作为Solutio Problematis ad Geometriam situs针对性(一个与位置几何有关的问题的解决方案)发表在1741年的Commentarii Academy inoae Science arum Petropolitanae杂志上，并作为Solutio Problematis ad Geometriam situs针对性(位置几何问题的解决方案)发表在1741年的Commentarii Academy temae Science arum Petropolitanae杂志上。[3]在数学世界里有英文版本。

在数学史上，欧拉对Königsberg桥问题的解被认为是图论的第一个定理和网络理论的第一个真实证明。自古以来，人们就一直在考虑其他类型的组合问题。

此外，欧拉认识到关键信息是桥的数量和它们的端点列表(而不是它们的确切位置)，这预示着拓扑学的发展。实际布局和图形示意图之间的差异是拓扑与对象的刚性形状无关的思想的一个很好的例子。

因此，正如欧拉认识到的那样，位置的几何不是关于测量和计算，而是关于更一般的东西。这使传统的亚里士多德学派认为数学是数量科学的观点受到质疑。虽然这一观点符合算术和欧几里德几何，但它不符合拓扑学和现代数学中研究的更抽象的结构特征。[需要引用]。

哲学家们已经注意到，欧拉的证明不是关于抽象的或现实的模型，而是直接关于桥梁的真实安排。因此，数学证明的确定性可以直接应用于现实。[5]。

上面给出的问题的经典陈述使用了未识别的节点-也就是说，除了它们的连接方式之外，它们都是相似的。存在标识节点的变体-每个节点被赋予唯一的名称或颜色。

河的北岸是蓝王子的城堡，南岸是红王子的城堡。东岸是里奇大桥(Ritcher)或教堂的所在地；在中心的小岛上有一家加萨索(Gtheraus)客栈。

据了解，接下来的问题应该按顺序进行，并从原始问题的陈述开始：

在加萨索斯逗留了几个小时后，镇上的居民习惯于尝试走桥，许多人已经回来吃更多的茶点，声称成功了。然而，没有人能够在白天重复这一壮举。

桥8：蓝王子用图论的方法分析了小镇的桥梁系统，得出的结论是桥是不能走的。他设计了一个秘密计划，建造第八座桥，这样他晚上就可以从他的学校开始，步行过桥，最后到达加萨索斯，吹嘘他的胜利。当然，他希望红王子不能重现红堡的胜利。蓝王子把第八座桥建在哪里？

第9桥：红王子被他哥哥戈尔迪安解决问题的方案激怒了，他想要建造第九座桥，这样他就可以从他的学校开始，走上桥，最后到达加萨索斯，在他哥哥的脸上抹上泥土。作为一种额外的报复，他的兄弟应该不能再像以前那样从他的学校开始走桥，到加萨索斯结束。红太子把第九座桥建在哪里？

第10桥：主教沮丧地看着这座疯狂的桥梁建造。它扰乱了小镇的世界观，更糟糕的是，还助长了过度酗酒。他想建造第十座桥，让所有的居民都能走上桥，回到自己的床上。主教在哪里建造第十座桥？

像以前一样，将城市缩小到一个图表。为每个节点上色。与经典问题一样，不可能出现欧拉漫游；着色不会影响这一点。所有四个节点的边数都是奇数。

桥8：如果正好有零个或两个节点具有奇数个边，则可以进行欧拉遍历。如果我们有2个边数为奇数的节点，则漫游必须从一个这样的节点开始，在另一个节点结束。由于拼图中只有4个节点，所以解决方案很简单。所需的漫游必须从蓝色节点开始，在橙色节点结束。因此，在其他两个节点之间绘制了一条新边。由于它们以前都有奇数个边，因此现在它们必须有偶数个边，才能满足所有条件。这是奇数到偶数的奇偶性变化。

9号桥：一旦8号桥解决了，9号桥就容易了。其愿望是启用红色城堡并禁止将蓝色城堡作为起点；橙色节点仍然是行走的终点，而白色节点不受影响。要更改红色和蓝色节点的奇偶校验，请在它们之间绘制一条新边。

10号桥：10号桥把我们带到一个略有不同的方向。主教希望每一位公民都能回到自己的起点。这是一个欧拉电路，要求所有节点的次数为偶数。在求解第9桥后，红色和橙色节点具有奇数次，因此必须通过在它们之间添加新的边来改变它们的奇偶性。

最初的七座桥中有两座在二战期间哥尼斯堡的轰炸中没有幸存下来。另外两座后来被拆除，取而代之的是一条现代化的高速公路。其他三座桥仍然存在，尽管其中只有两座是欧拉时代的(一座是1935年重建的)。[6]因此，截至2000年，五座桥梁存在于涉及欧拉问题的同一地点。

根据图论，其中两个节点现在的阶数为2，另外两个节点的阶数为3。因此，欧拉路径现在是可能的，但它必须在一个岛上开始，在另一个岛上结束。[7]。

位于克赖斯特彻奇的坎特伯雷大学在老物理图书馆和厄斯金大楼之间的草地上加入了一个桥梁模型，这里是数学系、统计系和计算机科学系的所在地。[8]河流被矮小的灌木丛取代，中央岛屿有一块石头tōrō。罗切斯特理工大学(Rochester Institute Of Technology)将这个拼图融入了吉恩·波利塞尼中心(Gene Polisseni Center)前的人行道上，吉恩·波利塞尼中心是一个于2014年开放的冰球场。[9]。

莱昂哈德·欧拉(1736年)。解决问题和解决相关的几何问题(Solutio Problematis and Geometriam Sitriam Situsientis"；)。评论。阿卡德。SCI。U.Petrop 8,128-40。

^Shields，Rob(2012年12月)。文化拓扑：哥尼斯堡的七座桥，1736"；理论、文化与社会。29(4-5)：43-57。10.1177/0263276412451161。希尔兹提供了对欧拉参与这一流行问题的社会意义的讨论，以及它作为(原始)拓扑理解应用于日常生活的一个例子的意义。

“复杂网络的结构和功能”(PDF)。密歇根大学物理系。

J·富兰克林，“亚里士多德的现实主义数学哲学”，帕尔格雷夫·麦克米伦，贝辛斯托克，2014年，第48-9、96、215、225页；J·富兰克林，“形式科学发现哲学家”，史学与科学哲学第25卷(4)(1994)，第313-533页。

彼得·泰勒(2000年12月)。那些桥到底发生了什么事？澳大利亚数学信托基金。2012年3月19日从原件存档。

关于坎特伯雷大学数学与统计。math.canterbury.ac.nz.。于2016年11月28日从原件存档。