锂中泡利晶体的可观性研究

费米-狄拉克统计学最著名的表现是泡利不相容原理：没有两个完全相同的费米子可以占据相同的单粒子态。这一原理在许多完全相同的费米子系统中实施高阶关联，即使在所有相互作用都不存在的情况下，这也是捕获粒子的特殊几何排列的原因。这些几何结构被称为泡利晶体，预测了囚禁在谐势中的N个完全相同的原子系统。在系统的单次拍摄图片集合中，它们是最常见的配置。在这里，我们研究当考虑到现实的实验限制时，泡利晶体的易碎性。考虑了可供分析的单镜头数、热起伏和检测效率有限等因素的影响。给出了这些噪声源对泡利晶体实验观测可能性的影响，并确定了探测粒子几何排列的必要条件。

超冷原子不仅为模拟各种多体量子系统1、2、3、4、5、6提供了理想的操场，也为研究少体物理提供了理想的平台。7.在超冷原子控制和监测方面取得了前所未有的进展，开辟了一个全新的可能性世界。例如，通过单位寻址技术8，可以在晶格系统的Mott绝缘相中获得原子数涨落得到充分抑制的受控少体系统。或者，可以在单个微阱9、10中确定性地制备少体系统。可以在定义良好的高保真量子态中制备1-10个费米子原子的小系统。

最近发展起来的单点荧光成像技术是监测多体系统11，12，13，14，15，16，17，18的重大突破。这项伟大的成像技术可以同时确定所有单个原子在单点分辨率12，13的光学晶格中的位置。单个孤立陷阱内的原子系综的快照可能包含许多关于该系统的关键信息。在这方面非常重要的是高阶空间关联，这对于单粒子探测来说是难以捉摸的，但可以从N体概率密度19、20、21、22中揭示出来。最好的例子之一是最近的实验22，在实验22中，通过比较系统的许多单镜头图像，显示了在玻色-爱因斯坦凝聚中创建的里德堡多体系统中自发自组织有序的检测。

实验进展挑战理论。用单粒子分辨率观测的量子多体系统引起了物理学家的兴趣，因为它们提供了不仅最常见的单体测量，而且两点关联也不能获得的信息。理解需要描述超越两点相关性的过程的例子相当多。它们包括例如种子纸23，其中示出了在N体检测过程中出现的干涉条纹。相反，在一体图像中看不到干扰。类似地，孤子出现在一维玻色子系统的第二类激发态中，该系统通过由Lieb-Liniger模型24描述的短程势相互作用。这些孤子是由于系统中的高阶关联而出现的，并且可以在单次探测多个原子时被发现。25中的工作演示了如何基于多体薛定谔方程的数值解来模拟一般超冷玻色子系统的单炮实验。对监测多体动力学的随时间变化的单次图像进行了模拟，揭示了有吸引力的BEC中的脉动涡旋的出现，提出了26条建议。

在这篇文章中，我们研究了少体系统中的另一个高阶关联的例子。我们感兴趣的关联完全是由于量子统计和不可区分性。全同粒子的不可区分性质导致了量子物理学中非常重要的结果。即使在没有任何相互作用的情况下，它也会固有地强加粒子之间的关联。事实证明，当许多零温的完全相同的费米子被困在外部的二维谐波陷阱中时，这些粒子会以一种惊人的方式自我定向，揭示出特定的几何结构，即泡利晶体。我们最近展示了如何从多体系统27的多张单镜头图像中提取这些几何结构。通过对大量数据的适当分析，给出了清晰、毫不含糊的泡利晶体图像。然而，有一个问题是，观测到的图像受到各种实验缺陷的影响有多大，以及泡利晶体的存在是否能得到实验证实。最近类似的泡利结构

其中\({{\mathcal H}}_{n}\)是\({n}^{th}\)Hermite多项式，\({\mathscr{N}}={{\mathrm{(2}}^{n+m}n！m！\sqrt{\pi})}^{1/2}\)是归一化常数。量子数n和m分别枚举x和y方向的激发。我们使用自然谐振子单位\({a}_{0}=\sqrt{\hslash/M\omega}\)，其中M是粒子的质量。与量子态\({\psi}_{Mn}\)相对应的单粒子能量为\({E}_{Mn}=(m+n+\mathm{1)}\hslash\omega\)，每个能级都是\((m+n+\mathm{1)})倍简并的。

在N体基态下，所有相同的费米子原子占据最低的可用单粒子量子态，直到费米能量。这是由于泡利不相容原理，该原理禁止它们占据相同的量子态。如果费米能级的状态数超过必须位于那里的粒子数，则基态不是唯一定义的。然而，在特定情况下，当N = 1、3、6、10、15、…。，相应系统的多体基态是非简并的。显然，泡利晶体的几何形状是给定状态的特征。如果能量没有唯一地规定状态，我们就会有各种不同的状态和几何构型对应于给定的能量。非零温度解决了这个问题。所有相同能量的状态对热密度矩阵的贡献是相等的。这里，为了简单起见，我们将讨论限于各向同性陷阱和完全占据的费米面。

基态能量是占据态的单粒子能量之和，\({{\mathcal E}}_{0}^{N}/\hslash\omega={\sum}_{i}^{N}({m}_{i}+{n}_{i}+\mathm{1)})。请注意，由于多体基态波函数\({{\rm{\psi}_{0q}^{N}({{\bf{r}_{1}，{{\bf{r}_{2}，\ldots，{{\bf{r}_{N})与单粒子轨道相关联的任何两组给定的\(({m}_{i}，{n}_{i})\)不可能相同，因为多体基态波函数\({{\rm{\psi}})_{0q}^{N}({{\bf{r}_{N}通过斯莱特行列式，占据的单粒子态。({{\Rm{\Psi}{0q}^{N}\)中的下标\(q\)解释了N体基态的简并。当系统处于基态时，\({{\mathscr{P}_{q}^{N}\)在\({{\bf{r}_{1}，{{\bf{r}_{2}，\ldots，{{\bf{r}_{N})\)发现粒子的概率为：

最大\({{\mathscr{P}_{q}^{N}\)，式。(2)，容易获得。例如，可以通过使用蒙特卡罗算法31找到它，其中，从随机选择的初始构型开始，通过移位原子位置来提出另一构型。如果配置比前一个配置更有可能，则接受移动。

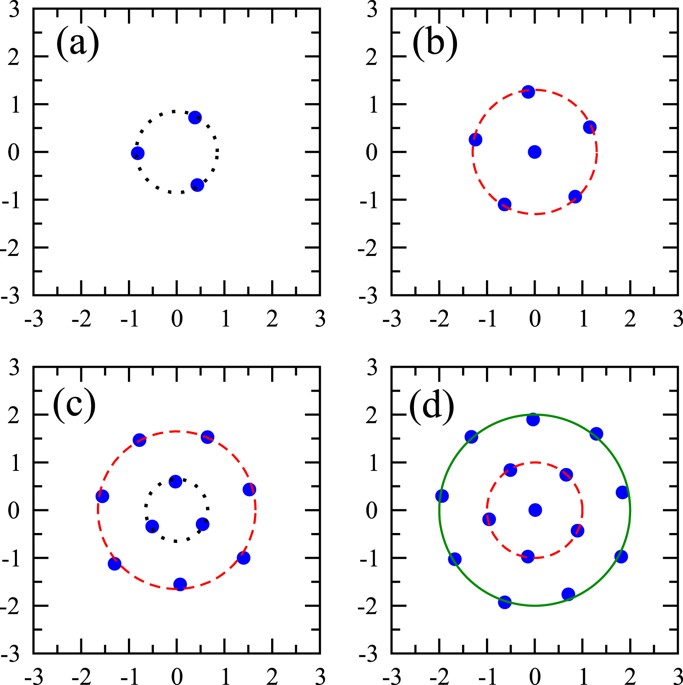
结果表明，正如27中所示，原子的最可能排列在零温度下表现出独特的几何结构。N = 3、6、10和15的这些构型如图1所示。三个原子在一个等边三角形的顶点上定向。在N = 6中观察到一种双壳层结构，其中一个原子位于陷阱中心，代表第一个(最内层)的壳层，第二个壳层由五个原子排列在一个五边形中形成。N = 10构型呈现出双壳结构，分别具有三角形和七角形，形成内壳和外壳。对于N = 15个原子，出现了第三个壳层，其中一个原子占据陷阱中心，相等间距的5个和9个原子形成第二个壳层，第三个(最外面的)壳层。可以看出，壳体的相对方向相对于彼此是刚性的。但是，每个结构作为一个整体都可以旋转，而不会影响\({{\mathscr{P}_{Q}^{N}\)的值。

二维谐振阱中相同费米子形成的晶体结构。蓝点表示通过最大化(A)3个原子、(D)6个原子、(E)10个原子和(F)15个原子的N粒子概率而获得的最可能的构型。黑色虚线、红色虚线和绿色实心圆分别表示第一个壳(最里面)、第二个壳和第三个壳。当第一个壳层由存在于中心的单个原子组成时，它会缩小到一个点。

我们假设占据谐波陷阱的原子的位置可以高分辨率地确定，比它们之间的间隔大，它们的间隔是振子单位长度的数量级。这个假设在这个时候是相当乐观的。目前，原子荧光显微镜的分辨率高于晶格间距，可以区分不同位置的原子。然而，要解决驻留在同一地点的原子的位置是不可能的。为了解决这个问题，原子应该在探测它们的位置之前被释放。只有在某种程度上展开后，才能区分原子。然而，弹道膨胀不会改变初始排列的几何形状。对于谐波约束展开d

实际上，同时重复测量N个原子的位置\({x}_{i}^{s})的L的直方图定义为：

其中索引s指的是不同的测量值。如果粒子的位置x与位于X处的探测器的位置以精度\({\rm{\Delta}}\)重合，即如果在X周围的体积\(V={{\rm{\Delta}^{2}\)中发现粒子，则函数\(\Delta({\bf{x}}-{\bf{X}})\)等于1。在相反的情况下，函数\(\Delta({\bf{x}}-{\。显然，H({\bf{X}})与量子力学单粒子概率分布成正比。这可以通过改变求和的顺序来看出来。直方图没有关于粒子位置相关性的信息，因为配置上的求和可以针对每个粒子独立完成。这将擦除有关系统中粒子和几何体的相对位置的信息。

如果我们手头既没有关于系统的信息，也没有关于它的对称性的信息，那么我们就不得不参考条件概率。在对测量结果进行处理之前，对每个构形进行移位，并将其几何中心定位在坐标系中心是非常有用的。这样就消除了质心位置的量子不确定性。寻找最可能构型的算法是基于后选择的，分为三个步骤。(I)要收集单次拍摄的图像，必须找到构型的直方图，即单粒子概率密度，并确定其最大值。(Ii)在下一步中，假设第一个粒子位于单粒子密度最大值(或更好地在预先设定的距离内，最大值为\(\varepsilon\))，则应找到条件概率。为此，在后选择过程中，我们只收集符合上述标准的单张照片。这些构型的直方图给出了两点条件概率密度。(Iii)假设第三个粒子的位置在这个最大值，我们可以重复选择后的过程，并构造三点条件概率。整个过程必须重复，直到找到所有N个最大值。在条件概率有几个局部极大值的情况下，如果存在全局极大值，则应该选择全局极大值，或者选择任何等价的极大值。

为了说明基于条件概率的这一过程，在图2中，我们显示了上述针对\(N=3)个原子的连续步骤的结果。在第一幅图(A)中，显示了消除质心不确定性后的单粒子概率密度。由于这种消除，密度在中心有一个最小值，并在环上达到最大值。然后，我们选择环上的一个点，并且只保留其中有粒子的图片距离所选点的距离小于\(\varepsilon\)。在图2中，我们设置\(\varepsilon=0.2\)。这样得到的两点条件概率密度如图(B)所示。可以看到两个相等的最大值。在第三个面板(C)中，我们展示了通过后选择获得的三点条件概率。可以看到三体几率密度最大的泡利晶体构型。在40K超冷系统32的实验中，到目前为止只观察到了两点关联函数，但高阶关联也在实验范围内。

条件概率密度。(A)去除质心不确定性后的单粒子密度，(B)两粒子条件概率密度，(C)三粒子条件概率密度。

如果系统具有某些对称性，则上述过程是非常浪费的。许多测量值可能仅仅因为它们的对称变换不同而从图片集合中删除。在图2(A)中，拍摄了一些\(L={10}^{7}\)快照，而通向图2(C)的过程仅留下\(7\x{10}^{4}\)个快照。我们研究的系统具有一定的对称性，我们将使用另一个图像处理过程27。让我们注意到，在每一次测量中，单粒子密度的旋转对称性被不同程度地破坏。每个测得的构型代表一整类构型，它们只是在对称变换上有所不同。我们希望利用这些对称性，将所有单次拍摄的图片与最大化N体概率的图片进行比较。在这里，我们假设了解手头的系统，我们知道零温下的几何排列，即泡利晶体的几何形状，假设其顶点位于\({\bf{r}_{0}\}}_{N}=\{\bf{r}_{01}，{{\bf{r}_{02}，\ldots，{{\bf{r}_{0n}。后者可以从理论上得到。然后将与特定测量实现相对应的所有单次结果\({\{\bf{x}}\}}_{N}=\{\bf{x}_{1}，{{\bf{x}_{2}，\ldots，{{\bf{x}_{N}\}\)与

..