ZkSNARK入门第1部分：什么是ZkSNARK

2009年比特币的引入将更多的研究注意力转向了广义区块链，隐私问题反过来又导致了寻找使区块链更加私密化的方法，但直到零比特币的引入才导致了ZCash的出现，证明了实用的零知识证明已经存在，并导致了密码学特别是密码原语的寒武纪爆炸，这自然导致了高度可扩展的去中心化系统。

关注的中心是由Goldwasser，Micali和Rackoff在1985年引入的零知识证据。一则有趣的轶事是，他们最初的论文早在1982年就发表了，但在1985年的计算理论研讨会之前，一直被各种会议拒绝。

通常被描述为“月球数学”的这些结构令人着迷和有用，主要有两个原因。第一个原因是零知识，可以翻译成私人的，证明是关于一个性质或定理真实性的陈述。

从戈德雷奇的“零知识”发明20年后：*“零知识证明”这一术语可以被视为相互矛盾的，因为这些证明具有很强的说服力，但除了被证明的陈述的有效性外，不会产生任何信息。*。

要开始理解这些，我们需要理解几个源于复杂性理论的关键概念。第一个概念是计算和语言，计算机用来做什么，我们可以证明什么样的陈述，第二个概念是归约和关注从一个问题转移到另一个问题的想法。

在这篇文章中，我们将主要讨论需要遵循的预备和基础知识，在后续的文章中，我们将回顾最新的证明系统，并讨论实现细节。

计算是任何类型的计算，包括遵循预定义模型(算法)的算术和非算术步骤。计算机之所以这样命名，是因为在最低级别，它们所做的只是算术运算和更简单的非算术运算。

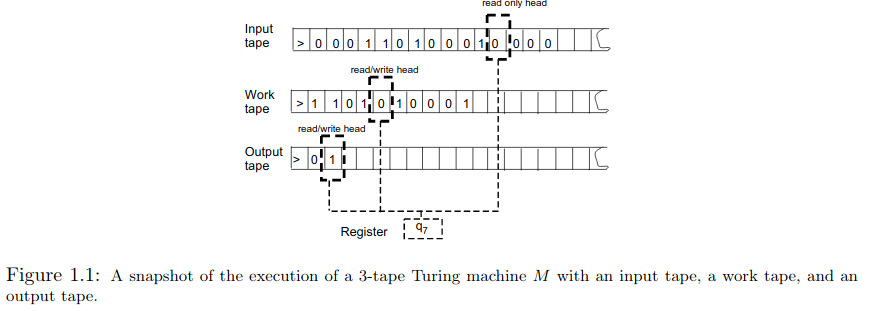
图灵机是计算机的理想化抽象，由一个单元阵列组成，称为包含位的磁带。我们可以使用任意数量的磁带，用于输入、临时变量和输出.

图灵机读取位序列，解释它们，如果通过基本指令，则执行基本指令。

考虑将两个数字相加的最简单示例，输入磁带将包含以二进制形式写成的a和b，例如0110||1101，其中“||”表示分隔符。代码磁带将包含单个操作“+”，机器的指针将遍历输入，读取操作并将结果写入输出磁带，这里不涉及复杂的计算，非算术操作通常是按位操作、逻辑条件检查或跳转，其中指针将跳过几个单元。

这可能看起来令人费解，因为如果你注意到定义本身并没有解释解释部分。如果你思考一下口译在这里意味着什么，你就会面临这样一个问题：机器里的幽灵是什么，是谁自己做口译。

考虑重影的一种方式是，它是一个电路，使用布尔电路和门(AND、XOR、NAND、NOT)，您可以计算任何您想要计算的长度。假设您想要计算您将读取的字符串的长度，将计数逐位存储在索引99处的单元格中，并使用加法电路(下面的更多内容)来递增它，直到您读取序列0000，这将标记字符串的结尾。

位和布尔运算-在CPU的引擎盖下有几个执行算术运算的布尔电路，例如加法器，实际上你可以构建布尔电路，它们非常普遍，你可以用你喜欢的语言将它们实现为代码。

现在我们这里是最重要的，电路足以进行大多数计算，事实上所有的计算都可以简化为一串电路。为了我们的目的，他们可以模拟图灵机。

现在给出这张图像，我们可以做几点评论，第一是电路足以做一系列的操作，第二是我们可以在计算执行时拍摄一张“照片”，换句话说，我们可以在机器执行我们指定的指令时捕捉机器的状态。

如果我们有一台图灵机并插入一个输入x，我们可以在它执行时捕获它的状态(磁带内容和指针位置的副本)。然后我们可以建立一个电路，模拟机器在输入x上所做的事情。这个漂亮的结果是普遍证明可能的一个主要原因。

在计算复杂性理论领域，决策语言仅仅是一个语句或序列，对于该语句或序列，存在一个见证者和一个多项式时间算法，使得当该算法插入到图灵机中时，机器根据该见证者对于语句实例是否正确而写入0或1。

诸如“x==5”、“图G是否有圈C”等语句都是决策语言的示例。我们说图灵机在输入语言L上接受，如果机器在执行后输出1，则见证w。

例如，如果L为“x==5”，w为6，则机器将输出0，如果w等于5，则机器将接受见证。

虽然这个定义可能看起来很复杂，但它的意思是，决策语言是一个存在足够快的算法的问题，比如对于正确的输入，它返回1，而对于不正确的输入，它返回0。

这里的问题是，NP语言是一种被认为是不可判定的语言，或者没有已知的多项式时间算法来解决它，但有一个有效的算法来验证可能的解(我们称之为见证)。

复杂性理论所关心的问题，是这样的问题，没有已知的有效算法来寻找解决方案。技术上称为NP-完全。其中一个问题称为电路可满足性或SAT。SAT问题是这样提出的：

您有一组由基本布尔门组成的布尔约束，例如AND、NOT、OR…。如果您选择这样做，您的任务应该是查找布尔变量的赋值(基本上从集合{0，1}中找到a，b，c的正确值)，例如约束求值为true。

你为变量找到的赋值就是我们所说的见证，要满足的公式就是输入。虽然找到解似乎很容易，但没有已知的算法可以做到这一点，这是一个悬而未决的问题。解决它会间接证明P=NP，并在此过程中为你赢得一百万美元的奖金。

来自NP-完全问题的一个自然现象是，可以用决策语言(主要是计算结果为1或0的函数f(x，y))形式表示的所有其他问题都可以转换为SAT。

这一自然性质实际上就是我们所说的约化，或者更确切地说，是我们上面松散定义的卡普-莱文约化。

现在CS理论中的一个重要发现指出，每一种“NP语言都有一个零知识证明”(Goldwasser，Micali和Wigderson证明了这一点)，换句话说，任何关于一个可以归结为SAT的问题的陈述都有一个零知识证明，即对于隐藏证人w和隐藏输入x SAT(x，w)，高概率地求值为1。

近年来的研究表明，二次跨度规划和以二次算术规划为自然推广的跨度规划都是NP-完全的，因此对这类问题等价地存在零知识证明。匹诺曹13号和最近的格罗斯16号都是这类问题的证明系统。

这些问题QSP、SSP、QAP被认为是类NP的特征，这意味着可以用决策语言(求值为1或0的函数)的形式描述的每个问题都可以简化为这样的实例。

我们之所以使用涉及代数和算术电路的问题(像布尔电路，但使用数字而不是位和算术运算而不是布尔电路)是因为我们在代数中有更多的数学工具，如椭圆曲线、双线性对，更重要的是多项式，我们知道如何从这些工具中构建密码方案，也知道如何高效地进行数学运算。

到目前为止，我们只窥视了一些与CS理论不同的概念，现在重要的问题是，在零知识中能证明什么？

从上面我们知道，有零知识证明可以证明NP中每种语言的成员资格，事实上，任何可以归结为其中之一的问题都可以在零知识中证明。

例如，值域证明提出这样的问题“is x in the range\([0，2^v]\)”其中v是某个随机整数，这样的陈述可以转化为关于两个向量的内积的代数问题，并且对于这样的问题，存在一个零知识协议Bootle等人。

让我们尝尝这种简化的滋味，我们知道范围\([0，2^v]\)中的任何值x都可以写成长度为v的二进制字符串。如果我们认为该二进制字符串是一个向量，那么证明\([0，2^v]\中的x\)归结起来就是证明三件主要事情：-设a=bin(X)，即x的二进制表示：-首先，我们需要证明\(=x\)这等同于基数转换检查(。s实际上等于x。-其次，我们需要证明\(a\cic(a-1)=0\)，其中\(\cic\)是Hadamard分量的明智乘积，以证明\(a\)确实是1和0的向量。最后，如果我们取\(al=a\)和\(ar=a-1\)，则我们需要证明\((al-1)-ar=0\)。

这三个约束现在是关于向量的陈述(约束)，我们可以将其折叠为检查多项式的等价性，如果我们加上一些随机性，得到的是x在[0，2^v]中的证明，以使它成为零知识，我们使用密码学的技术(Pedersen承诺和随机盲因数)。

项目符号证明就是区块链应用程序中用来隐藏交易金额的证明的一个这样的例子。

在区块链应用领域，我们通常想要证明的语句对snark非常友好(某些曲线的签名验证例如参见Jubjub或Merkle Tree成员资格证明，这些对电路非常适用)例如，用zokrate编写的Schnorr电路将一个框架编译为电路的小Ocaml语言。

这种自然的变换使我们能够利用代数工具进行零知识证明，其中一个工具是多项式。关于多项式的推理比关于电路的推理要容易得多，而且往往更有效。这就是我们将电路(R1CS)转换为QAP以建立更简洁的证明系统的原因之一。

因为我们想要证明的大多数陈述都很容易验证，而且可能很难生成(前映像、加密值……)。零知识证明在加密货币和区块链中的应用相当多。

事实上，让我们看一下涉及Merkle证明的熟悉的例子，例如，考虑事务已经花费了一个输入的证明“TxID=x的事务#5已经花费了块#9的散列=y的输入”，证明这一点的一种方法是提供输入的审计路径、事务的审计路径和相应的头部。

Merkle证明的验证算法主要涉及散列运算，因此可以采用递归算法，将其展开为一系列约束进行验证。

A的审核路径包括*[H(B)，H(H©，H(D))，R]，其中R是树的根。要验证A确实在这三个值中，我们需要计算H(A)，然后计算H(H(A)，H(B))，依此类推，直到得到根表达式。

为了将所述运算转换为算术电路，我们需要256阶域(以覆盖散列输出)，然后给定计算散列函数的电路，我们有一系列以A为输入的子电路，作为见证的审计路径计算散列，然后检查最终约束Merkle(A，AP)==R。

我们面临的问题是，并不是所有的散列函数都可以编译成算术电路，而不是在大小不变的情况下。这就是为什么最近我们看到了Snark友好的密码散列函数，如MIMC或Rescue，它们的操作可以有效地转换为算术电路，而不像SHA256，它涉及几个布尔操作。

程序的算术化(即将计算编译成算术电路或代数系统)可以通过两种方式完成，第一种模型使用我们刚刚看到的电路，第二种模型将整个虚拟机简化为电路检查。TinyRAM，El-Sasson等人著。是一种这样的实现方式，

TinyRAM有一组有限的指令，TinyRAM程序可以简化为算术电路，反之亦然，您可以在本文中找到更多详细信息。

尽管如此，既然我们在这里，让我们来看看如何将在RAM模型(配备内存的图灵机)中运行的程序转换为电路可满足性问题。

假设我们有一个虚拟机，其中RAM是一个字数组，并且我们为这台机器配备了一组k个寄存器，如上所述，我们可以捕获机器的照片或跟踪，您可以将跟踪看作是在执行的每个步骤中其寄存器和内存的带有时间戳的快照序列。

粗略地说，在每条指令中，我们保存寄存器{R1，R2，R3.}和RAM[W1，W2，W3.]的快照，现在让我们假设我们向VM提供一个由指令(操作码)和执行VM的输入x组成的程序，该VM通常输出一个位串y。

我们转换成电路的是每个操作码的逻辑，然后我们将输入提供给电路，对照该步骤的状态内容检查输出并继续。我们不想被骗运行无限循环，因此我们通常有固定大小的状态快照，并通过计算时间戳的数量来获得时间限制，如果电路到那时还没有完成，我们就会拒绝它。

当转换为电路可满足性问题时，电路然后将被给予见证，在这种情况下，见证是执行的轨迹，候选输入x是程序的输入，并且所有的电路将做的是检查该轨迹确实是正确的执行轨迹，并且它将在{0，1}中输出y。

检查子电路的输出是否等于见证(i+1)这等同于检查操作码是否为正确的转换。

RAM模型有点复杂，对于最简单的问题往往具有非常大的状态，但是没有RAM的简单模型(例如堆叠机)更适合这种转换。

一旦程序算术化或代数化，进行密码学就变成了选择原语的问题，这里再次出现了权衡。证明系统(通常参考密码部分)将需要可信设置来生成参数(公共参考字符串)，并且在某些情况下，证明系统可能不是通用的(即，对于您想要证明的每个程序或电路都需要新的可信设置)。

第二个是证明大小与安全假设之间的权衡，使用更强假设的方案往往具有较小的证明，而STARK依赖于底层哈希函数的抗冲突性，证明大约为200KB。而Groth 16的证明系统，其改为使用双线性配对，具有200字节大小的证明。

按照同样的思路，Groth16需要为您想要证明其执行的每个程序设置一个受信任的设置，而Starks则不需要任何设置。

这就是更新的证明系统的亮点，如Plonk，它是通用的和可更新的(需要对所有程序进行一次设置，直到电路界限，并且设置本身可以顺序地在多方设置中完成)。

附注：-snarks中的“A”代表参数，可以理解为该方案对于计算受限的证明者是安全的，具有无限计算能力的证明者可以为错误陈述提供有效的证明。-snarks中的Succintness意味着证明大小小于我们希望证明的电路(或语句)，并且验证器所做的工作小于电路大小的工作。-snarks是由一组算法(GEN、PROMPE、VERIFY)定义的协议-上面讨论的NP减少步骤。这就是为什么“参数”只对计算绑定的证明者是安全的原因之一。

在讨论一些用于部署的snarks(如ZCash)的密码工具之前，我们需要讨论零知识证明的安全性，从敌意的角度讨论它们的性质，更重要的是，我们需要讨论它们所遵循的假设。

稳健性：如果没有证明者可以欺骗验证者接受错误的证明，除非概率为\(\epsilon\lll 1\)，则称证明系统为\(\epsilon\)-健全。

完备性：如果对于所有有效的证明，验证以概率1成功，则称证明系统是完整的。

当我们谈论安全假设时，我们通常指的是所使用的密码学的基本计算问题。例如，离散对数假设指出，非量子对手很难找到下面的离散对数(g^x=y\)，其中\(g\)是有限群的生成器。

这一假设是现代Ellptic Curve密码体制所依据的，因为曲线上的点自身组成一组，例如以素数为模的整数与曲线点互换，因此假设成为\(SG=P\)，其中\(s\)是下层素域的标量，\(G\)是曲线点组的生成器(也称为基点)，\(P\)是曲线上的点。

一般来说，一个系统做的假设越少，它被计算能力强大的对手破解的可能性就越小。

在配对的情况下，离散对数假设和计算Diffie-Hellman假设在具有量子能力的对手下都被打破，同样的情况也适用于在黑暗中使用的隐藏有序群，它退回到强RSA假设，其中指数可以不同于3。

唯一已知的抵御具有量子能力的对手的系统是STARK，因为这些系统使用与Snark不同的结构(IOP和PCP而不是QAP，并且是相当信息论的问题)，STARK唯一需要的是抗冲突的哈希函数。

Fiat Shamir启发式是一种用于使交互式协议成为非交互式的技巧。在交互式协议中，想法很简单。验证器向证明者发送随机质询，这些质询要么用于查询证据，如在PCP或IOP中，要么用作多项式运算的某种输入，在这两种情况下，我们都需要随机字节。

您如何才能使交互不需要发生，但仍然强制验证器生成随机性，而不是使用选定的输入？

答案一如既往地是散列函数。这个想法是这样工作的，你创建一个成绩单，它只是一个字符串序列，证明者从证明系统输入参数，可能还有一些字符串，每当他需要一个随机的字节序列时，他就会通过哈希函数传递整个成绩单。

统一的散列函数在生成随机数据方面做得很好，验证者可以使用记录来检查自己使用的随机值是否正确，只需重新运行记录即可。

这是一次快速而肮脏的行走-通过对zkSNARK的总体想法，为什么我们粉饰了许多细节，我们试图停留在较新作品的框架内，强烈邀请读者自己调查历史和文学。

阿维·威格德森(Avi Wigderson)的“数学与计算”一书是世界上另一个伟大的

..