《180子午线》(2016)

180度子午线横跨俄罗斯、斐济、南极洲、两海三洋，是一个几何奇迹，也是一个地理和技术上的老大难问题。它与投影、解释和界面问题交织在一起。这就是为什么在一些地图上有一条穿过俄罗斯的线。你可能已经在与肮脏的180度搏斗了，想知道整个故事的来龙去脉。不管怎样，我们开始吧。

地理位置通常存储为数字：经度和纬度，表示为-180到180经度和-90到90度之间的度数。在典型的世界地图上，-180经度是地图最左边、美洲的左边的线，180经度是俄罗斯、中国和澳大利亚的最右边的线。

在地图的顶部有数据：包括点、线和多边形的几何形状。点仅由经度、纬度对标识。线是经度、纬度位置的列表。多边形也是循环中经度、纬度位置的列表。

在你想要放在地图上的许多东西中，有一些旅行，比如飞行路线，可以绕地球一周，穿越180度子午线。

有些软件将-180到180范围之外的经度值视为无效，如经度=300。

你如何表示一条横跨180度子午线的线？如何表示与180度子午线重叠的多边形？

直觉上看，这些地方彼此都很近。第一个是伦敦，第二个是伯明翰。如果让你在这两者之间划一条线，可能会是这样的：

从第一个点到第二个点的方向是北和东。如果你想在这两个数字之间找到一个位置，你可以将这些数字求平均：

那是在英格兰的另一个地方，大致在两个地方之间，不值得注意，它可能很古怪，但它是无关紧要的。

得出一个结论：当两地之间距离180度子午线较近而较远时，它们之间的界线似乎很明显，一切都很容易。

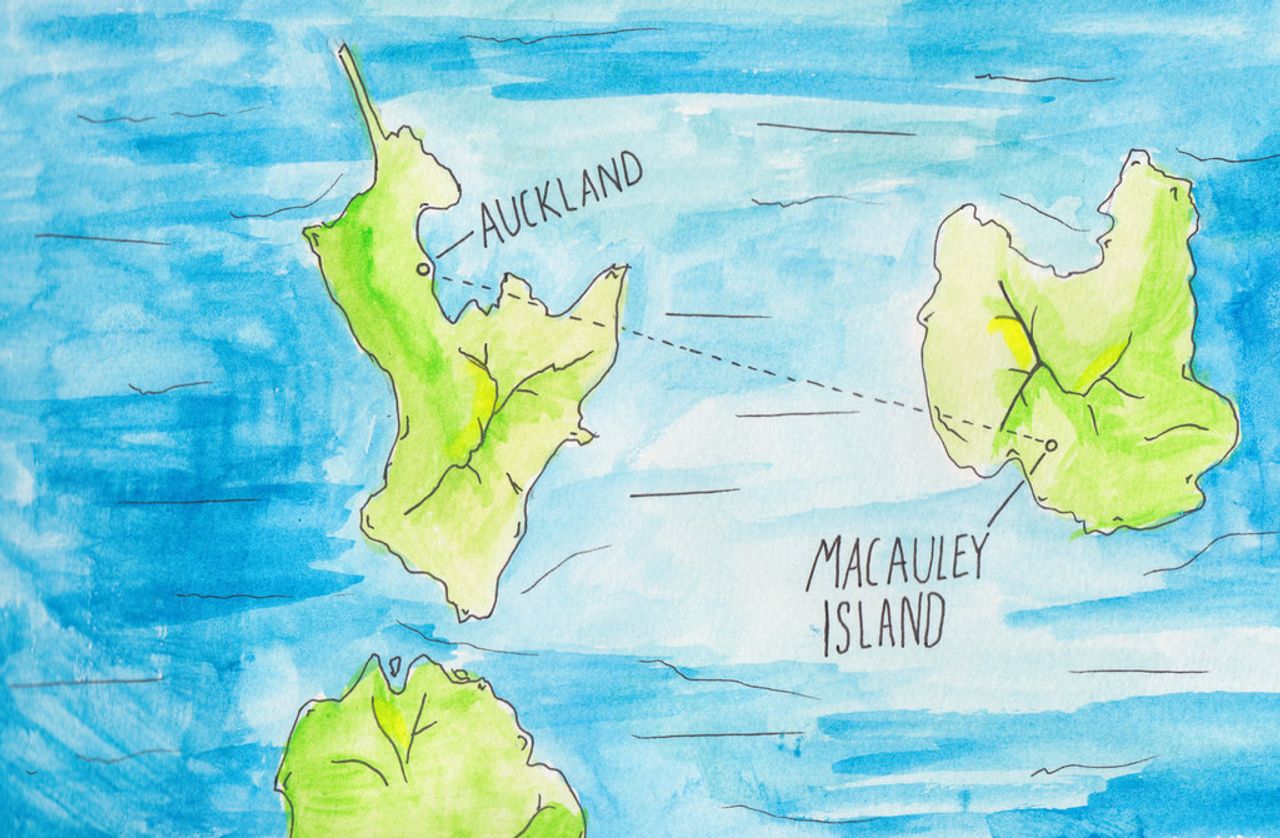
没有刻度或者没有准确地画出。事实上，麦考利应该在奥克兰以北，这是不准确的。但是画水彩画很有趣。

如果你要在这两个地方之间划一条线，你有两个选择：“一路穿过”，或者跳过180度子午线。如果你用一个简单的平均值在它们之间找一个点，

作为人类，走远路似乎是不对的：最短的路是常识。这是我们在现实生活中使用的假设：如果我的朋友从巴尔的摩到华盛顿特区旅行，我会假设他们会沿着高速公路行驶45英里，而不是乘坐飞机环游世界。

有人给你看他们手中的一枚硬币，头朝上。他们转过身，抛硬币，然后再给你看硬币，再一次把头朝上。它翻了几次？

人手中硬币的角度不是一个绝对数，它抛得越多就越高。不，每次硬币旋转360度，它又在同一个地方。

同样，当你在滑板上完美地执行720双踢腿翻转，或者更有可能是在视频游戏中，你最终会回到开始的地方：滑板面朝前。如果你的朋友错过了你的成就，一切都一样。

回到手头的问题：我们如何表示跨越180子午线的特征？

您可以尝试编写软件来猜测-179和179是否试图相互跳转：本质上模拟人类的判断。有些软件试图做到这一点，偶尔也能满足人们的期望。事实上，苹果在MapKit的某些部分就有这种行为。

但它也有真正的缺点：识别180街的跳数既棘手又固执己见。一旦你创造了一些“神奇”的行为，自动连接通常不会连接的线路，就会变得更难表现这样的情况：有人出于某种深奥但非常可能的原因，想要代表从新西兰到新西兰另一个岛屿的漫长的飞行路线。

多年来，这一直是我个人偏爱的方法。例如，如果你想从奥克兰向东旅行到麦考利岛，而不是从经度174.76398到-178.43054，你可以从174.76398到181.56946：这两个数字在数学上非常接近。要做到这一点，您需要将其中一个数字加或减360度，直到它接近数字行上的另一个数字。

这也有不利的一面，不仅仅是200多个经度值看起来很奇怪。许多使用地理数据的程序和库都会很高兴地显示以这种方式表示的180度子午线交叉几何图形，但有些程序和库会拒绝-180、-90、180、90框之外的值，要么将其裁剪并隐藏，要么完全无法避免未定义的行为。

这就是你可能在早些时候在OpenStreetMap上看到的方法-这就是为什么俄罗斯在OpenStreetMap上有一条难看的线穿过它的原因。

要点是：给定一个通过180子午线的几何体，将其切片并切割，直到有多个不与子午线交叉的几何体。在GeoJSON和许多其他格式中，可以使用多部分几何图形(如多重线串和多重多边形)拆分几何图形，而无需复制有关它们所描述的要素的信息。

在表示穿过反偏线的要素时，通过修改它们的几何图形来提高互操作性。任何穿过反分割线的几何图形都应该通过将其一分为二来表示，使得任何部分的表示都不会与反分割线交叉。-GeoJSON规范，3.1.9

与其他解决方案不同的是，这个解决方案既没有“魔力”或直觉，也很安全：这种编码不会被其他软件拒绝或曲解。所以它很容易被正确地解释，而且是安全的。

“折痕”问题。制图软件通常绘制与分层线串和多重多边形完全相同的多重线串和多重多边形要素。因此，如果您必须拆分您的线条并且这些线条有开始和结束标记，或者您拆分一个多边形并且它有一个边界，那么在最终的渲染中可能会有一个边界。

分线并不明显。看起来很明显：要找到中点，单位是度，你可以将一个坐标偏移360，直到它在数字线上接近另一个坐标，找出两个坐标之间的角度，然后从东边的点到180度子午线的距离就是直角三角形的底部或顶部，然后你做高中阶段的三角试验就可以到达那里。记住索卡托。

但是经纬度的中点是正确的吗？在很多情况下，情况并非如此。

如果您在等矩形投影中显示地图，它看起来会很正确，但很少有人使用该投影。它很好，因为它与经度和纬度直接相关，但在大多数其他制图方面没有做到这一点。

如果在Web墨卡托投影中显示地图(很可能是这样)，并使用经度和纬度在中点处分割一条线，则会得到一条曲线，除非一侧位置的纬度与另一侧的纬度完全相同。线条短的时候，曲线不会很明显，但线条长的时候，曲线就会很明显。

GeoJSON Spec推荐的技术可能是最好的方法。它将更多的责任交给了数据生产者，并避免了任何无效数据的可能性。但是它本质上并不容易实现-如果您通过LEAFLE的GeoJSON图层类型向Web地图动态添加一条线，那么计算180子午线上的分割点是很棘手的。一个包含这种复杂性的库很可能会冒出来。

不管规范的建议是什么，180很可能会对未来的地图制作者构成挑战，不管具体的技术选择如何。对于大多数地理学来说，将经度和纬度作为存储信息的手段是一个根深蒂固的假设，而将旋转的3D地球上的位置转换成数字和图片总是不完美和令人担忧的。

细心的读者可能会从抛硬币的例子中收集到一个想法：我说过，你不能说出硬币抛了多少次，因为它的角度是一个绝对数字，而不是相对于旧位置的数字。

大多数地理空间格式以绝对形式存储坐标：每个坐标都被完整记录，因此它被编码为，例如，-72，24，无论它是作为一个点还是作为线中的一个位置出现。

还有另一种方式：增量编码，或“相对编码”。使用增量编码，不是用绝对数存储每个坐标，而是将第一个位置的绝对位置存储在比方说一行中，然后存储该位置的增量(更改)。例如，如果一行开始于-72，24，而不是存储：

这在一定程度上回避了-180问题，因为跨越180子午线的直线可以编码为：

也就是说，您将直线存储为一系列向量，而不是一系列绝对位置。因为矢量是有方向的，所以你知道你是要跳过180度的短距离，还是要走很长的路。

您不能读取或修改线或面中的任意坐标，因为它相对于它之前的所有坐标，并且它之后的所有坐标都会受到影响。

这种编码很聪明，但是不受欢迎：您需要经常在编码之间进行转换，所以每次都会有最低公分母的特征胜出。

有增量编码的实例-Mapbox矢量平铺和TopOJSON都使用该技术-MVT是一种表示格式，TopOJSON主要将其用作效率制胜，而不是实际的功能差异。

那不是叫国际日期变更线吗？不完全是。国际日期变更线与180度子午线有很多重叠之处，但它不是一条直线。它蜿蜒曲折，以至于俄罗斯和斐济完全在一边，其他岛屿的形成没有被这条线分开。

为什么180度子午线在那里？嗯，焦点一直集中在本初子午线上，它一直在移动，直到最后以格林威治为中心，艾里爵士谦虚地选择了他的小镇作为世界的中心。

当地的基准呢？(对于外行来说，除了经度和纬度之外，还有其他方法来表示地球上的地方-基本上是一个小型的测量系统，可以从一个城镇的某个参考点测量英尺，而不是整个世界的度数)。好的，那么，是的！有一些基准面横跨180度，因此可以让您干净利落地保存穿过它的东西。但是，顾名思义，本地数据是本地的：它们通常不能以任何有意义的方式应用于整个世界，因此它们在通常是全球优先的新软件世界中并不是特别受欢迎。

想知道180度切割线的三角解是如何工作的吗？敬请关注明天的一集。