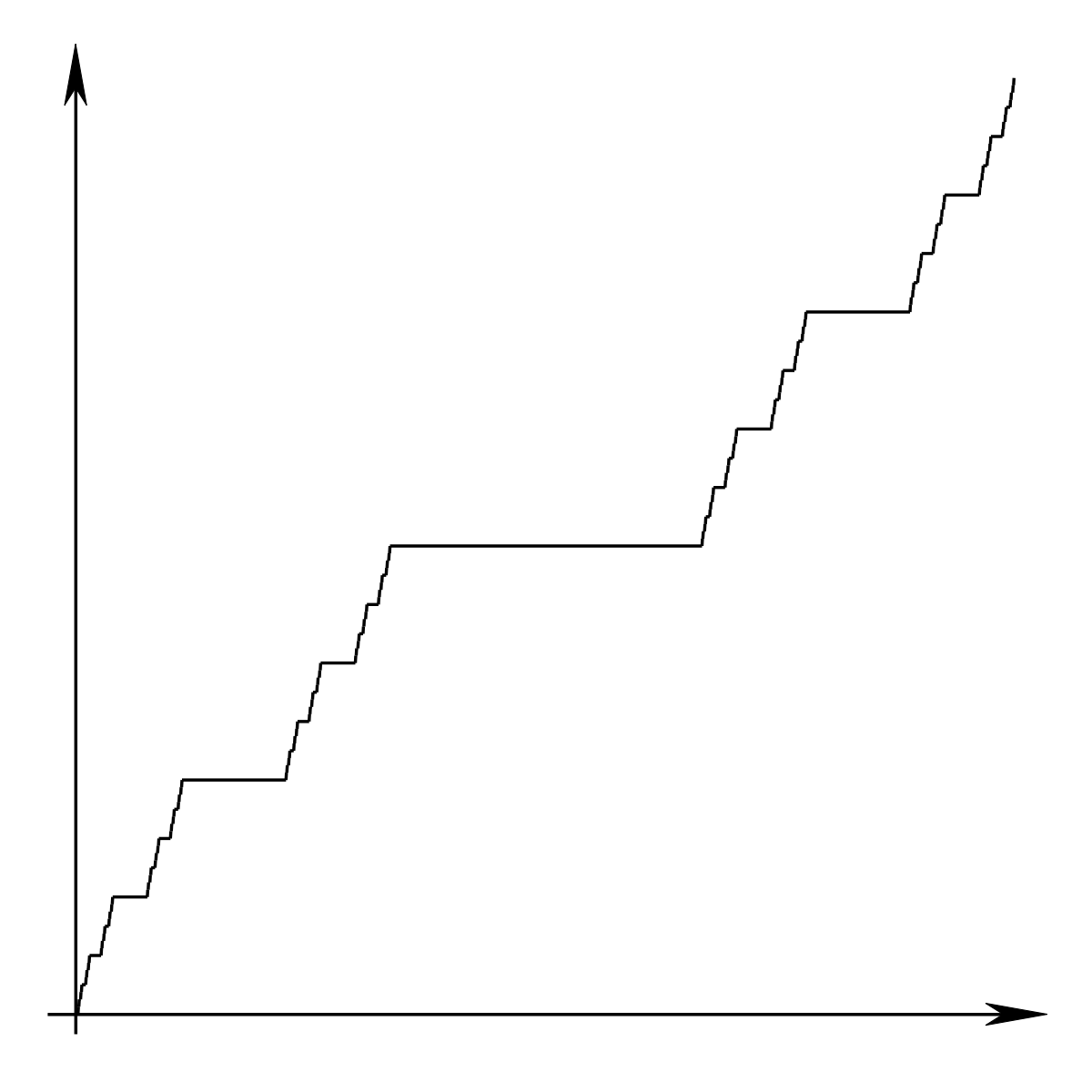
康托函数，又名。魔鬼阶梯：0导数的递增函数

跳转到导航跳转在数学中搜索，康托函数是一个连续的函数，但不是绝对连续的。这在分析中是一个臭名昭著的反例，因为它挑战了关于连续性、导数和测度的天真直觉。虽然它处处是连续的，几乎处处都有零导数，但当它的自变量从0到1时，它的值仍然从0到1。因此，从某种意义上说，该函数看起来非常像一个常数，不能增长，而在另一种意义上，它确实是通过构造单调增长的。

它也被称为康托三元函数，勒贝格函数，[1]勒贝格奇异函数，康托-维塔利函数，魔鬼楼梯，[2]康托楼梯函数，[3]和康托-勒贝格函数。[4]Georg Cantor(1884)引入了Cantor函数，并提到Scheeffer指出它是Harnack所声称的微积分基本定理的推广的反例。康托函数由Scheeffer(1884)、Lebesgue(1904)和Vitali(1905年)讨论和推广。

参见图。要正式定义康托函数c：[0，1]→[0，1]，设x在[0，1]中，通过以下步骤获得c(X)：

如果x包含1，则将第一个1后面的每个数字严格替换为0。

1/4是0.02020202.。在基数3。没有1所以下一阶段仍然是0.02020202…。这里改写为0.01010101..。当以基数2读取时，这对应于1/3，因此c(1/4)=1/3。

1/5是0.01210121.。以3为基数。第一个1后面的数字被0替换成0.01000000…。因为没有2，所以不会重写。当以基数2读取时，这对应于1/4，因此c(1/5)=1/4。

二百/二百四十三等于0.21102(或0.211012222.)。以3为基数。第一个1之后的数字被0替换为0.21。这被重写为0.11。当以基数2读取时，这对应于3/4，因此c(200/243)=3/4。

等价地，如果C{\DisplayStyle{\Mathcal{C}}是[0，1]上的康托集，则康托函数c：[0，1]→[0，1]可以定义为

C(X)={∑n=1∞a n 2 n，x=∑n=1∞2 a n 3 n∈C f o r in a n∈{0，1}；sup y≤x，y∈C c(Y)，x∈[0，1]∖C.。{\displaystyle c(X)={\start{case}\sum_{n=1}^{\infty}{\frac{a_{n}}{2^{n}}，&；x=\sum_{n=1}^{\infty}{\frac{2a_{n}}{3^{n}\in{\mathcal{C}}\\maththm{for}\a_{n}\。\sup_{y\leq x，\，y\in{\mathcal{C}c(Y)，&；x\in[0，1]\setminus{\mathcal{C}}。\end{case}。

这个公式是明确定义的，因为Cantor集合的每个成员都有一个唯一的基数为3的表示法，该表示法只包含数字0或2。(对于C{\DisplayStyle{\mathcal{C}的某些成员，三元展开与尾随的2'；s重复，并且存在以1结尾的替代非重复展开。例如，1/3=0.13=0.02222.。3是康托集合的成员)。由于c(0)=0和c(1)=1，并且c在C{\displaystyle{\mathcal{C}上是单调的，显然，0≤c(X)≤1对[0，1]中的所有x∈[0，1]∖C{\displaystyle x\在[0，1]\set减{\mathcal{C}也成立。

Cantor函数挑战了关于连续性和测度的天真直觉；尽管它处处连续，几乎处处导数为零，但c(X){\textstyle c(X)}随着x{\textstyle x}从0到1而从0到1，并取其间的每个值。康托函数是实函数一致连续(确切地说，它是指数为α_2/log_3的Hölder连续)但不是绝对连续的最常被引用的例子。它在形式(0。x 1 x 2 x 3.。X N022222.，0.。x 1 x 2 x 3.。xn200000…)，并且每个不在康托集合中的点都在这些区间中，所以它的导数在康托集合之外是0。另一方面，它在包含上述区间端点的康托集的不可数子集中的任何点都没有导数。

康托函数也可以看作康托集上支持的1/2-1/2伯努利测度μ的累积概率分布函数：C(X)=μ([0，x]){\TextStyle c(X)=\Mu([0，x])}。这种概率分布称为康托分布，没有离散部分。也就是说，相应的度量是无原子的。这就是函数中没有跳跃不连续的原因；任何这样的跳跃都将对应于度量中的一个原子。

然而，康托函数的任何非常数部分都不能表示为概率密度函数的积分；在任何区间上积分不是几乎处处为零的任何假定的概率密度函数都将给该分布赋予概率零的某个区间以正概率。特别地，正如Vitali(1905)指出的那样，函数不是其导数的积分，即使导数几乎处处存在。

康托函数是非递减的，因此特别是它的图形定义了一条可校正的曲线。Scheeffer(1884)证明其图的弧长为2。

由于无穷大的康托集的勒贝格测度为0，对于任意正的ε，1和δ，都存在一个总长度为&δ的两两不交子区间的有限序列，在该序列上，康托函数的累计升幅大于ε。

事实上，对于每一个显示样式和限制_{k=1}^{M}(y_{k}-x_{k})<；δk=1M(y_k−x_k)<；δ；0都有有限多个两两不交区间(x_k，y_k)(1_DisplayStyle，y_k)<；\DELTA}和∑k=1M(c(Yk)−c(Xk))=1{\DisplayStyle\SUM\LIMITS_{k=1}^{M}(c(y_{k})-c(x_{k}))=1}。

下面我们在单位区间上定义一个收敛于康托函数的函数序列{fn}。

然后，对于每个整数n≥0，下一个函数fn+1(X)将根据fn(X)定义如下：

设fn+1(X)n=1/2+1/2×fn(3 x−2)，当2/3≤x≤1时。

这三个定义在端点1/3和2/3处是兼容的，因为通过归纳，对于每个n，fn(0)f=0和f n(1)f=1。可以检查fn是否逐点收敛到上面定义的康托函数。此外，收敛是一致的。事实上，根据fn+1的定义，分成三种情况，我们可以看到。

max x∈[0，1]|f n+1(X)−f n(X)|≤1 2 max x∈[0，1]|f n(X)−f n−1(X)|，n≥1.{\displaystyle\max_{x\in[0，1]}|f_{n+1}(X)-f_{n}(X)|\leq{\frac{1}{2}}\，\max_{x\in[0，1]}|f_{n}(X)-f_{n-1}(X)|，\quad n\geq 1。}。

max x∈[0，1]|f(X)−f n(X)|≤2−n+1max x∈[0，1]|f 1(X)−f 0(X)|.。{\displaystyle\max_{x\in[0，1]}|f(X)-f_{n}(X)|\leq 2^{-n+1}\，\max_{x\in[0，1]}|f_{1}(X)-f_{0}(X)|}。

此外，如果f0(0)i=0，f0(1)i=1，并且f0有界[需要引用]，那么起始函数的选择实际上并不重要。

康托函数与康托集密切相关。康托集合C可以被定义为区间[0，1]中在其基数-3(三元)展开中不包含数字-3\f25 1-3的那些数字的集合，除非1后面只跟零(在这种情况下，尾部-3\f25 1000-3\f25…-3\f6。{\DisplayStyle\ldots}可以替换为0222Dotts。{\displaystyle\ldots}以删除任何1)。结果表明，Cantor集是一个具有无穷多个点(零维体积)，但长度为零(一维体积)的分形。这里D=loglog(2)/loglog(3){\displaystyle D=\⁡(2)/\⁡(3)}是C的分形维数。我们也可以将康托函数定义为康托集合的截面的D维体积。我们可以把康托函数定义为康托集合的截面的D维体积，其中D=LOG Log(2)/LOG(3){\DisplayStyle D=\LOG(2)/\LOG(3)}。我们也可以将康托函数定义为康托集合的截面的D维体积

F(X)=HD(C∩(0，x))。{\displaystyle f(X)=H_{D}(C\cap(0，x))。}。

y=∑k=1∞b k 2−k{\DisplayStyle y=\sum_{k=1}^{\infty}b_{k}2^{-k}}。

是实数0≤y≤1关于二进制位b k∈{0，1}的二进(二进制)展开式。然后考虑函数。

Cz(Y)=∑k=1∞b k z k。{\displaystyle C_{z}(Y)=\sum_{k=1}^{\infty}b_{k}z^{k}。}。

对于z=C1/3，函数x=2的逆C1/3(Y)是Cantor函数。也就是说，yy=yy(X)是康托函数。一般而言，对于任何1/2的z，Cz(Y)看起来就像是Cantor函数侧翻，随着z接近于零，台阶的宽度也会变宽。

如上所述，Cantor函数也是Cantor集合上测度的累积分布函数。不同的康托函数，或魔鬼的楼梯，可以通过考虑不同的康托集或其他分形支持的无原子概率度量来获得。虽然Cantor函数几乎处处都有导数0，但目前的研究集中在右上导数与右下导数不同的点集的大小问题上，从而导致导数不存在。这种可微性分析通常以分形维数的形式给出，其中Hausdorff维数是最流行的选择。这方面的研究是由Darst在20世纪90年代开始的，他证明了Cantor函数的不可微集的Hausdorff维数是Cantor集维数的平方，(LOG⁡2/LOG⁡3)2{\DisplayStyle(\log2/\log3)^{2}}。随后，Falconer[6]证明了这种平方关系对所有的Ahlfor'都成立；的正则奇异测度，即dim H⁡{x：F‘(X)=L im H→0+μ([x，x+h])h不存在}=(dim H⁡supp⁡(μ))2{\displaystyle\dim_{H}\Left\{x：F'；(X)=\lim_{h\to 0^{+}}{\frac{\mu([x，x+h])}{h}}{\text{不存在}}\right\}=\Left(\dim_{H}\Operatorname{supp}(\mu)\right)^{2}}。

随后，Troscheit[7]获得了更全面的集合的图景，其中对于自共形和自相似集合上支持的更一般的归一化Gibb&#s测度，不存在导数。

赫尔曼·明科夫斯基(Hermann Minkowski)的问号函数在视觉上松散地类似于康托函数，看起来像是后者的平滑形式；它可以通过从连分式展开到二进制展开来构造，就像康托函数可以通过从三元展开到二元展开来构造一样。问号函数具有在所有有理数处导数为零的有趣性质。

理查德·达斯特(1993-09-01)。Cantor函数的不可微集的Hausdorff维数为[ln(2)/ln(3)]2"；美国数学学会论文集。119(1)：105-108。10.2307/2159830。联合包裹服务公司股价上涨2159830。

肯尼斯·J·福尔科纳(2004-01-01)。单边多重分形分析与魔鬼楼梯的不可微点。剑桥哲学学会数学论文集。136(1)：167-174。密码：2004MPCPS.136..167F。DOI：10.1017/S0305004103006960。ISSN电话：1469-8064。

^Troscheit，萨沙(2014-03-01)。自共形魔鬼楼梯的Hölder可微性。剑桥哲学学会数学论文集。156(2)：295-311。Arxiv：1301.1286。密码：2014MPCPS.156..295T。DOI：10.1017/S0305004113000698。ISSN电话：1469-8064。

巴斯，理查德·富兰克林(2013)[2011]。研究生真实分析(第二版)。CreateSpace独立出版公司。ISBN电话：978-1-4818-6914-0。CS1维护：REF=HARV(链接)。

康托，G.(1884)。de la puqhance des overfaits de Points：Extrit d&39；une lettre adresséeàl"；éditeur"；[完美点数的力量：从致编辑的信中摘录》(The Power of Perfect Set Points：Extrit d'；une lettre adresséeàl"；éditeur"；)。数学学报。波士顿国际出版社。4：381-392。DOI：10.1007/bf02418423.。ISSN：0001-5962。转载于：E.Zermelo(编辑)，Gesammelte Abhandlungen Mathatischen and Philosophischen Inhalts，Springer，New York，1980。

理查德·B·达斯特；朱迪思·A·帕拉加洛；普莱斯，托马斯·E(2010)，“好奇曲线”，哈肯萨克，新泽西州：世界科学出版公司。ISBN978-981-4291-28-6,2681574先生。

Dovgoshey，O.；Marto，O.；Ryazanov，V.；Vuorinen，M.(2006)。"；康托函数"；(PDF)。“数理演绎”(Exexextiones Mamaaticae)。爱思唯尔BV。24(1)：1-37。doi：10.1016/j.exmath.2005.05.002.。ISSN电话：0723-0869。2195181岁的先生。

朱利安·F·弗隆(1994-04-01)。关于康托集和康托函数历史的注记"；。数学杂志。Informa UK Limited。67(2)：136-140。10.2307/2690689。ISSN：0025-570X。联合包裹服务公司股价上涨2690689。

勒贝格，H.(1904)，Leçons sur l'；intégration et la recherche des Functions Priftions[关于整合和搜索原始函数的课程]，巴黎：Gauthier-Villars。

莱昂尼，乔瓦尼(2017)。索博列夫空间的第一堂课。181(第二版)。罗德岛普罗维登斯：美国数学学会。734页。ISBN电话：978-1-4704-2921-8。华侨城：976406106。

谢弗，路德维希(1884)。Allgemeine Untersuhungenüber Constraint der Curven"；[关于曲线校正的一般调查]。数学学报。波士顿国际出版社。5：49-82。DOI：10.1007/bf02421552.。ISSN：0001-5962。

首页--期刊主要分类--期刊细介绍--期刊题录与文摘--期刊详细文摘内容。初等实数分析(第二版)。ClassicalRealAnalysis.com。ISBN电话：978-1-4348-4367-8。CS1维护：REF=HARV(链接)。

Vestrup，E.M.(2003)。测度论和整合论。概率统计中的威利系列。约翰·威利和他的儿子们。ISBN978-0471249771。CS1维护：REF=HARV(链接)。

维塔利，A.(1905)，#34；Sulle Funzioni Integrali"；[关于积分函数]，Atti Accad.。SCI。都灵属(Torino Cl.)。SCI。菲斯。垫子。自然，40：1021-1034