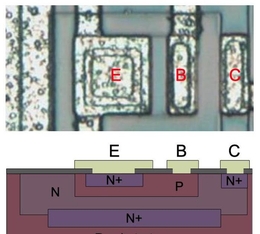
逆向工程Snapchat(第二部分)：对Undeobfuscatable进行去模糊处理

许多黑客新闻用户建议使用仿真来生成令牌，将整个事情视为一个黑匣子。正如我在评论中提到的，这个解决方案的问题是有太多真实的设备依赖。X-Snapchat-Client-Auth-Token不是随机胡言乱语。它包含很多关于设备的加密信息。即使您使用Corellium，我也只能说它工作的机会微乎其微。除了扭转它，我看不到其他选择。

首先，所有这些怪物是如何实现的？当您使用clang编译hello.c时，clang只是前端，llvm才是真正的代码；这意味着clang获取C源代码并将其转换为中间表示(IR)1，然后llvm解释该IR，优化并将其编译为机器码。这个系统的优点是后端仍然与语言无关，您只需为每种语言编写一个与LLVM-IR兼容的前端，其余的留给llvm。现在我们感兴趣的是优化，也就是优化过程。llvm对IR进行操作以生成更高效的代码，这些代码在汇编语言中看起来可能与您预期的略有不同，这就是产生混淆的原因；我们可以随心所欲地更改代码，只要我们保持语义，而不是实际优化代码。这就是O-LLVM2在编译器级别的工作方式，因为没有人能像那样维护源代码。(O-LLVM背后的团队现在被Snap3收购了)如果我们理解混淆，难道我们不能反其道而行之，生成类似于原始程序集的东西吗？正如一位Hackernews用户4所阐述的那样，模糊处理大多是有损的；您可以随意去模糊(许多很酷的库5允许您这样做)，但是直接接触二进制文件要好得多。

“Evan Spiegel讨厌这个把戏！”：或者，如何绕过断点检查。

这可能会结束我的Snapchat逆转职业生涯(或者实际上是整个帖子)。这个二进制文件的最大障碍之一是FUKUP_DEBUGING。因此，您将无法进行任何类型的动态分析(在我看来，这是在这个二进制文件中进行的唯一方法)。而且，您不能修补FUKUP_DEBUGING以返回正确的PATH_KEY，从而使其执行正确，而不是无限循环，因为有反篡改检查来阻止您以修改后的二进制文件与服务器通信。但是首先，您如何才能获得正确的path_key呢？根据定义，您必须设置一个断点，这样您才能在第一时间进入FUKUP_DEBUGING。是死锁吗？让我们来看看它的运行情况：在这里，我们在返回令牌的函数中，这是调用FUKUP_DEBUGING的块，我知道这是因为当我调试它时，紧随其后的块是一个无限循环。

mov x8，#0x4458movk x8，#0x1e6，LSL#16movk x8，#0x1，LSL#32movk x8，#0x0，LSL#48mov x9，#0x4714movk x9，#0x1e6，LSL#16movk x9，#0x1，LSL#32movk x9，#0x0，LSL#48add x1，x1FUKUP_DEBUGING调用adrp x8，0x109e5b000ldr w8，[x8，#0x6a8]EOR w8，w8，w0；返回path_keycmp x8，#0xborr w9，wzr，#0x6csel x8，x9，x8，Hildrx8，[x28，x8，lsl#0x3]br x8。

如果您像我一样聪明，并且在禁用所有断点之后，使用(Lldb)ni而不是单步执行跳过funkup_debuting，您将得到一个无限循环，因为您刚刚设置了另一个断点。这是因为跳过实质上是下一条指令地址处的断点。虽然单步执行有自己的小ptrace命令(Ptrace_SINGLESTEP)6，或者换句话说，它在CPU级别执行，但没有代码修补。

FUKUP_DEBUGING的弱点是它自己不检查断点。这就是为什么您可以在其中无害地设置断点的原因。在那里，未来的Snap反向工程师在修补了这个之后面临着新的挑战。

现在，我们已经为一个函数绕过了一个断点检查。并非令牌生成中的每个函数都是断点检查的。但是现在，对于使用上述方法绕过的每个检查，您可以使用正确的路径键添加注释。因此，在未来，这将是一个问题：

我们跳过FUKUP_DEBUGING并动态修补返回值。我们的速度有点慢，因为我们必须对每个打补丁的函数执行此操作，但现在我们至少可以进行一些真正的调试。

下面是令牌在非常高的级别上发生的情况。我们有联合函数gen_Token，它调用set_Token_params，这是一个调用许多其他函数的庞大联合函数。然后，令牌被加密并从gen_Token返回。要获得这样的信息，您必须花一些时间进行二进制运算，并进行有根据的猜测，直到您有了一个大致的总体情况，然后您可以选择一些具体的东西，或者采用自下而上的方法来使其简明扼要。让我们来看一个如何反转特定令牌参数的示例。

在二进制文件的关键区域设置书签将为您节省大量时间，并让您头疼不已。例如，我在写入令牌参数的位置有书签，就在令牌被加密之前，等等。这样，我只需知道某个参数在令牌结构中的偏移量，就可以开始处理该参数，因为这是我所知道的最接近其生成位置的跟踪。但是，您首先是如何找到这些锚地址的呢？

如果您让我只给您一个词来解决您一半以上的Snap二进制问题，我会告诉您：观察点。例如，您不知道从哪里开始，但是您知道gen_Token返回令牌的指针，所以这是您的领先位置。然后在gen_Token返回之前跟踪它，您会发现该指针在gen_Token返回之前实际上是由另一个函数写入的，比如等效的C代码：

现在，在调用real_deal之前，您在TOKEN_OUT上设置了一个观察点，禁用所有断点，以便FUKUP_DEBUGING满意，然后继续执行，然后观察点将在写入/读取过程中停止该进程，将您带到代码的一个可能的临界点，您可以将其用作锚点。这是我用Snap二进制获得的第二张A。

(Lldb)w s e-w写入--$x0(Lldb)c.。现在，一旦访问了$x0处的地址，并且您有了锚地址，它就会停止。

观察点是不错的，但是寄存器呢？你不能在这些上面设置观察点，或者理论上你可以，但那是另一次了。那么，如果您感兴趣的值在寄存器中，那又如何呢？答案是执行跟踪和支持regex的文本编辑器。

假设我们在set_Token_params中，并且我们知道我们感兴趣的值在x2中：

因为这是块的开始，没有cfg，所以我们不知道x2是从哪里来的。

我所做的是使用Frida的Stalker 7从SET_TOKEN_PARAMS附近的一个点生成一个执行跟踪，我知道这个点不是由FUKUP_DEBUGING管理的；因为Frida修补指令以挂钩到函数，这将触发断点检查。现在我有了一个连续的行刑轨迹。然后，我使用一个很好的旧文本编辑器来查找上面的块，并搜索它之前的点，即写入x2的位置和数据源所在的位置。

一旦您发现某个参数是由函数gen_param1生成的，我就别无选择，只能将其反转为其高级源代码等效项。我认为C(哈哈)最适合这一点，因为您可以准确地将数据结构/类型从汇编转换为C。而且，尽管C离CPU很近，但您仍然需要了解结构对齐是如何工作的，对某些值及其类型进行合理的猜测，并跟踪所有堆栈偏移。在处理这个二进制代码的时候，我梦到了汇编指令，没有狗屎。

MBA表达式是这个二进制代码中最棘手的事情。关于MBA的最新研究表明，有两种有效的方法可以简化MBA的表达方式。让我们解释一下，然后给出一个二进制代码的例子。

在此方法9中，您将整个表达式视为一个黑盒“Oracle”，为其提供输入，观察输出，并尝试生成一个模拟该行为的函数。这样做最大的问题是，它对于复杂的表达式8来说是不切实际的。

在此方法8中，所有简化规则都是硬编码的，例如，您有一个规则：(x|y)-y+(~x&；y)==x^。然后，您尝试递归地将规则与表达式匹配，然后使用SMT解算器来证明原始表达式与简化色调相同。这样做的问题是，规则不像布尔/代数简化那样通用，因此它无法处理硬编码之外的表达式。

第一步是从二进制文件中提取表达式，我们可以使用符号执行10。这基本上是一种执行二进制文件的方式，我们不给变量赋值，只给符号赋值。非常适合这一点的是令人惊叹的Triton 11框架。提取表达式后，对于合成，您仍然可以使用Triton 12，而对于重写规则，QuarkSlab提供了SSPAM 13，它仅是Python 2。

此示例涉及120多个指令块，其输入是来自堆栈的两个值，其输出位于4个寄存器中。最棘手的输出在x27中，所以我们将使用它。首先，我们需要提取表达式。我们使用Triton.symbizeMemory对块的输入进行符号化，然后在模拟块之后，使用Triton.getSymbolicRegister(x27).regAst().unroll()，获得寄存器中的完整表达式，准备打印到：

(0x431e33362537db49|(~(0xbac03a4c7e26a10c^((0xbac03a4c7e26a10c&；(~(Bss_Val1)&；0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff)|(bss_val1&；(~(0xbac03a4c7e26a10c)&；0xffffffffffffffffff。0xffffffffffffffffffff))|(bss_val1&；(~(0xbac03a4c7e26a10c)&；0xffffffffffffffffffffffffffffffffffffffffffffff))&；0xffffffffffffffffffffffffffff))&；0xffffffffffffffff)&；(~(0xc92460b4173d8。0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff)(~(0xc92460。0xffffffffffffffff)|(bss_val1&；(~(0xbac03a4c7e26a10c)&；0xffffffffffffffffffffffffffffffff))&；0xffffffffffffffffffff)|(~(0x431e33362537db4a|(~(Bss_Val1)&；0。0xffffffffffffffff)|0x253a41858a5c76d6)-(0x431e33362537db49|(~(0xbac03a4c7e26a10c^((0xbac03a4c7e26a10c&；(~(Bss_Val1)&；0xffffffffffffffffffff)|(bss_val1&。(~(Bss_Val1)&；0xffffffffffffffffffffffff)|(bss_val1&；(~(0xbac03a4c7e26a10c)&；0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff)&；0xffffffffffffffffffff)&；(~(。0xffffffffffffffffffffffffffff)-(~(Bss_Val1)&；0xffffffffffffffffffffffffffffffffffffff)&；0xffffffffffffffffffffffffffff))|(0x431e33362537db4a|(~(Bss_Val1)&；0xffffffffffffff))-(~(Bss_Val1)&。0xffffffffffffffffff)|(0x431e33362537db49|(~(0xbac03a4c7e26a10c^((0xbac03a4c7e26a10c&；(~(Bss_Val1)&；0xffffffffffffffffffffffffffffffffffffffffffffffffffff)|(bss_val1&；(~(0xbac03a4c7e26xbac03a4c7e26。0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff)。

真正的表达式没有那么可怕，因为Triton添加了位掩码。让我们看看SSPAM有什么要说的：

$sspam"；`cat x27_exprs`"；(4836359357488159561L|(~(13456819786791428364L^((13456819786791428364L&；(~bss_val1))|(bss_val1&；4989924286918123251L)。3952928246324163886L)^((14493815827385387729L&；(~(-(~bss_val1))+(4836359357488159562L|(~bss_val1)|(-(~bss_val1)+(4836359357488159562L|(~bss_val1)&；395。4989924286918123251L)|(~((-(~bss_val1))+(4836359357488159562L|(~bss_val1)^2682528569860323030L)。

那不太好。因此，SSPAM，我所知道的唯一存在的MBA重写规则的工具，并没有给出一个有意义的简化。所以我想让我们尝试一些合成，我使用Python的eval将不同的输入插入到这个表达式中，看看输出中的位有什么反应(自己试一下，很有趣)。最后，我合成的表达式是：

我看不出它会变得比这更简单，但是它与模糊的表达式相同吗？我们来问一下Z3：

令牌生成不只是迷惑。能够在这个级别使用二进制文件只是成功的一半。我不会的