实践操作线性规划：使用Python进行优化

2020-06-22 23:55:22

线性规划是数学规划中使用的一组技术，有时也称为数学优化，用于求解线性方程组和不等式系统，同时最大化或最小化某些线性函数。它在科学计算、经济、技术科学、制造、交通、军事、管理、能源等领域都很重要。

Python生态系统为线性编程提供了几个全面而强大的工具。您可以选择简单和复杂的工具，也可以选择免费的和商业的工具。这完全取决于你的需要。

您将首先了解线性规划的基础知识。然后，您将探索如何在Python中实现线性编程技术。最后，您将查看资源和库来帮助您进一步了解线性编程之旅。

免费奖励：关于Python掌握的5点想法，这是一门面向Python开发人员的免费课程，它向您展示了将Python技能提升到更高水平所需的路线图和心态。

在本节中，您将学习线性编程的基础知识以及相关学科混合整数线性编程。在下一节中，您将看到一些实用的线性编程示例。稍后，您将使用Python解决线性规划和混合整数线性规划问题。

想象一下，你有一个由线性方程和不等式组成的系统。这样的系统通常有许多可能的解决方案。线性规划是一组数学和计算工具，允许您找到此系统的特定解，该解对应于某个其他线性函数的最大值或最小值。

混合整数线性规划是线性规划的推广。它处理至少有一个变量取离散整数而不是连续值的问题。虽然混合整数问题乍看起来类似于连续变量问题，但它们在灵活性和精确度方面具有显著的优势。

整数变量对于正确表示用整数自然表示的数量非常重要，例如生产的飞机数量或服务的客户数量。

一种特别重要的整数变量是二进制变量。它只能取0或1的值，在做出是或否的决定时很有用，比如是否应该建造一座工厂，或者是否应该打开或关闭一台机器。您还可以使用它们来模拟逻辑约束。

线性规划是一种基本的优化技术，在科学和数学密集型领域已经使用了几十年。它精确、相对快速，适合于一系列实际应用。

混合整数线性编程允许您克服线性编程的许多限制。您可以使用分段线性函数近似非线性函数、使用半连续变量、建立逻辑约束模型等。这是一个计算密集的工具，但计算机硬件和软件的进步使它每天都更适用。

通常，当人们试图描述和解决优化问题时，第一个问题是他们是否可以应用线性规划或混合整数线性规划。

下面的文章说明了线性规划和混合整数线性规划的一些使用案例：

随着计算机能力的提高、算法的改进以及用户友好的软件解决方案的出现，线性规划(尤其是混合整数线性规划)的重要性随着时间的推移而增加。

解决线性规划问题的基本方法称为单纯形法，它有几种变体。另一种流行的方法是内点法。

混合整数线性规划问题是用更复杂和计算密集的方法来解决的，比如分支定界法，它在引擎盖下使用线性规划。这种方法的一些变体是分支切割法，它涉及到切割平面的使用，以及分支价格法。

有几个适用且广为人知的Python工具可用于线性编程和混合整数线性编程。其中一些是开源的，而另一些是专有的。您是否需要免费或付费工具取决于问题的大小和复杂程度，以及对速度和灵活性的需求。

值得一提的是，几乎所有广泛使用的线性编程和混合整数线性编程库都是由Fortran、C或C++原生编写的。这是因为线性规划需要计算密集的矩阵(通常很大)。这样的库称为求解器。Python工具只是解算器的包装器。

Python适合于围绕本机库构建包装器，因为它可以很好地与C/C++配合使用。本教程不需要任何C/C++(或Fortran)，但是如果您想了解更多关于这一很酷的功能，请查看以下资源：

基本上，当您定义和求解模型时，您使用Python函数或方法来调用执行实际优化工作并将解决方案返回给Python对象的低级库。

几个免费的Python库专门用于与线性或混合整数线性规划解算器交互：

在本教程中，您将使用SciPy和PULT来定义和解决线性规划问题。

与资源分配相关的实际问题，它说明了现实世界方案中的线性规划概念。

如果线性规划问题没有解，它就是不可行的。当没有解决方案可以同时满足所有约束时，通常会发生这种情况。

例如，考虑如果添加约束x+y≤−1会发生什么情况，那么至少有一个决策变量(x或y)必须为负。这与给定的约束x≥0和y≥0冲突。这样的系统没有可行的方案，所以叫不可行。

另一个示例是添加与绿线平行的第二个相等约束。这两条线没有共同点，因此不会有同时满足两个约束的解决方案。

一个线性规划问题是无界的，如果它的可行域不是有界的，解也不是有限的。这意味着您的变量中至少有一个是不受约束的，可以达到正无穷大或负无穷大，从而使目标也是无限的。

例如，假设您采用上面的初始问题，并删除红色和黄色约束。把约束从问题中去掉就叫做放松问题。在这种情况下，x和y不会在正值上有界。您可以将它们增加到正无穷大，从而产生无限大的z值。

在前面的小节中，您看到了一个抽象的线性规划问题，该问题与任何实际应用程序都不相关。在这一小节中，您将发现一个与制造业资源分配相关的更具体、更实用的优化问题。

假设一家工厂生产四种不同的产品，第一种产品的日生产量是x₁，第二种产品的日生产量是x₂，依此类推。目标是确定每种产品的利润最大化日生产量，同时牢记以下条件：

第一个、第二个、第三个和第四个产品的单位产品利润分别为20美元、12美元、40美元和25美元。

由于人力所限，每天的总产量不能超过50台。

对于第一个产品的每单位，消耗三个单位的原材料A。第二个产品的每单位需要一个单位的原料A和两个单位的原料B。第三个产品的每个单位需要一个单位的A和两个单位的B。最后，第四个产品的每个单位需要三个单位的B。

由于运输和储存的限制，工厂每天可以消耗多达100个单位的原材料A和90个单位的B。

目标函数(利润)在条件1中定义，人力约束来源于条件2，对原材料A和B的约束可以从条件3和条件4通过对每个产品的原材料需求求和得到。

最后，产品数量不能为负，因此所有决策变量必须大于或等于零。

与前面的示例不同，您不能方便地可视化这个示例，因为它有四个决策变量。然而，无论问题的维度如何，原则都是一样的。

在本教程中，您将使用两个Python包来解决上述线性规划问题：

本网站的设置很简单。一旦您安装了它，您就拥有了启动所需的一切。它的子包scipy.Optimize既可以用于线性优化，也可以用于非线性优化。

纸浆可以让你选择解算器，并以更自然的方式表达问题。纸浆使用的默认解算器是硬币或分支和切割解算器(CBC)。它连接到用于线性松弛的硬币或线性规划求解器(CLP)和用于切割生成的硬币或切割生成器库(CGL)。

另一个很棒的开源解算器是GNU线性编程工具包(GLPK)。一些著名且非常强大的商业和专有解决方案有Gurobi、CPLEX和XPRESS。

除了在定义问题时提供灵活性和运行各种求解器的能力外，与Pyomo或CVXOPT等需要更多时间和精力来掌握的替代方案相比，MPOT使用起来不那么复杂。

要学习本教程，您需要安装SciPy和PULT。下面的示例使用版本1.4.1的SciPy和版本2.1的MPT。

您可能需要运行Pulptest或sudo Pulptest才能启用纸浆的默认解算器，特别是在使用Linux或Mac时：

或者，您可以下载、安装和使用GLPK。它是免费和开源的，可以在Windows、MacOS和Linux上运行。在本教程后面的部分中，您将看到如何对纸浆使用GLPK(除了CBC之外)。

有关更多信息，请参阅GLPK关于使用Windows可执行文件和Linux包安装的教程。

在本节中，您将学习如何使用SciPy优化和寻根库进行线性编程。

linprog()只解决最小化(而不是最大化)问题，不允许带有大于或等于符号(≥)的不等式约束。要解决这些问题，您需要在开始优化之前修改问题：

您可以最小化z=x+2y的负值(−z=−x−2y)，而不是最大化z=x+2y。

可以将黄色不等式乘以−1，得到相反的小于或等于符号(≤)，而不是使用大于或等于符号。

这个系统等同于原来的系统，并且会有相同的解决方案。应用这些改变的唯一原因是为了克服与问题表述相关的本科学计划的局限性。

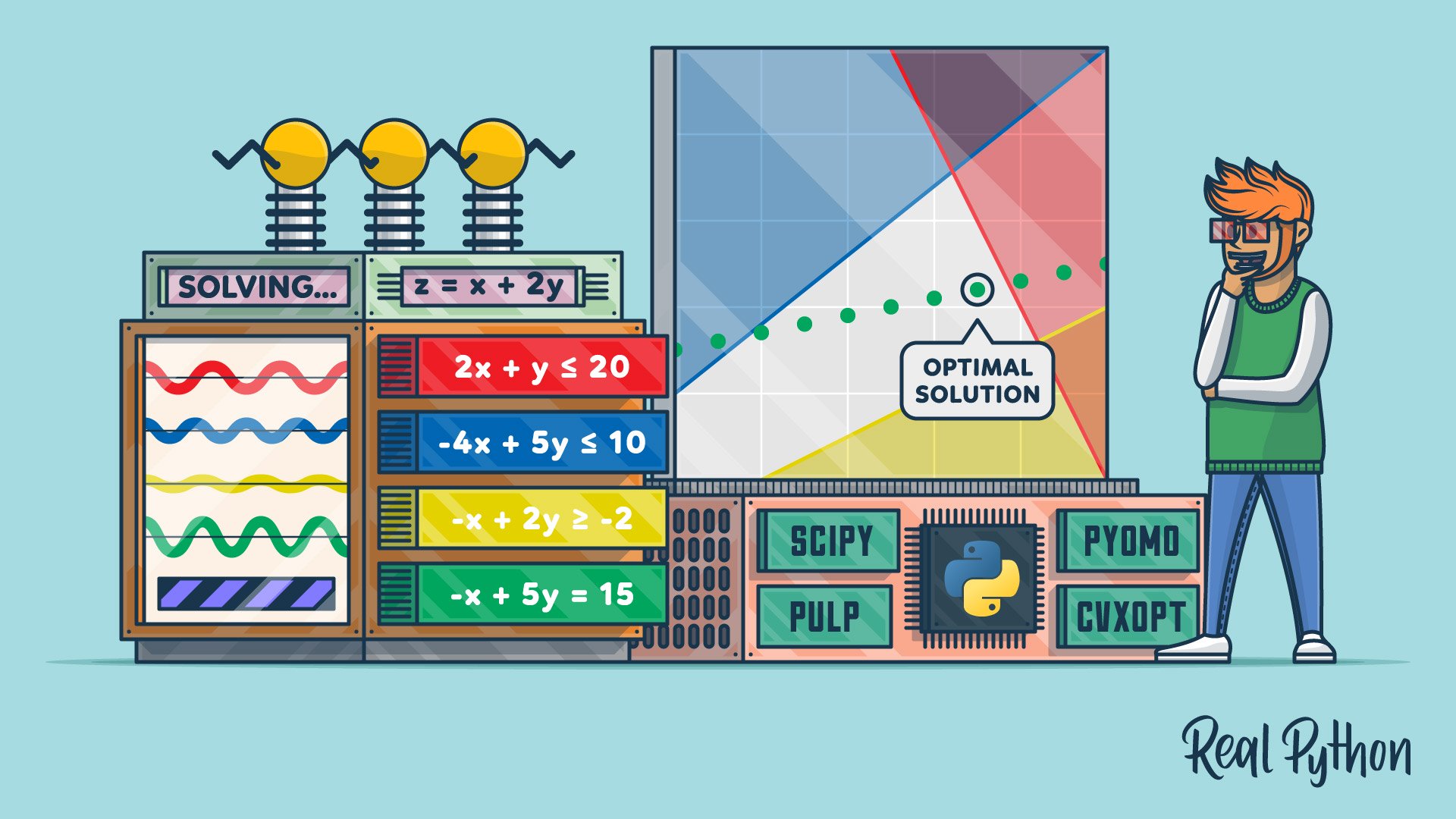
>；>；obj=[-1，-2]>；>；>；#─┬─┬>；>；>；#y>；>；>；#x>；>；>；#│└┤系数。lhs_ineq=[[2，1]，#红色约束左侧.[-4，5]，#蓝色约束左侧.[1，-2]]#黄色约束左侧>；>；>；rhs_ineq=[20，#红色约束右侧.10，#蓝色约束右侧.2]#黄色约束右侧>；>；lhs_eq=[[-1，5]]#绿色约束左侧>；>；>；rhs_eq=[15]#绿色约束右侧。

您可以将上述系统中的值放入相应的列表、元组或NumPy数组中：

约束左侧和右侧的行顺序必须相同。每行代表一个约束。

来自目标函数和约束左侧的系数的顺序必须匹配。每列对应于单个决策变量。

下一步是以与系数相同的顺序定义每个变量的界限。在这种情况下，它们都在零和正无穷大之间：

>；>；bnd=[(0，Float("；inf"；))，#x的边界.(0，Float("；inf"；))]#y的边界。

该语句是多余的，因为linprog()在缺省情况下接受这些界限(从零到正无穷大)。

最后，是优化和解决您感兴趣的问题的时候了。您可以使用linprog()执行此操作：

>；>；opt=linprog(c=obj，A_ub=lhs_ineq，b_ub=rhs_ineq，.。a_eq=lhs_eq，b_eq=rhs_eq，Bound=Bnd，.。method="；修订单纯形&34；)>；>；>；opt con：array([0.])。FUN：-16.818181818181817消息：'；优化已成功终止。'；NIT：3 SLACK：ARRAY([0.。，18.18181818，3.36363636])状态：0成功：真x：数组([7.72727273，4.54545455])。

参数C指的是来自目标函数的系数。a_ub和b_ub分别与不等式约束左侧和右侧的系数相关。类似地，a_eq和b_eq指的是等式约束。您可以使用界限来提供决策变量的下限和上限。

可以使用参数方法定义要使用的线性规划方法。有三个选项：

.slack是松弛变量的值，也就是约束的左侧和右侧的值之间的差值。

.status是一个介于0和4之间的整数，它显示解决方案的状态，例如，0表示找到最佳解决方案的时间。

这就是您获得优化结果的方式。您还可以以图形方式显示它们：

如前所述，线性规划问题的最优解位于可行域的顶点。在这种情况下，可行区域就是位于蓝线和红线之间的绿线部分。最佳解决方案是表示绿线和红线交点的绿色正方形。

如果要排除相等(绿色)约束，只需从linprog()调用中删除参数A_eq和b_eq：

>；>；opt=linprog(c=obj，A_ub=lhs_ineq，b_ub=rhs_ineq，bound=bnd，.。method="；修订的单纯形&34；)>；>；>；opt con：array([]，dtype=flat64)FUN：-20.714285714285715消息：'；优化已成功终止。'；NIT：2 SLACK：Array([0.。，0。，9.85714286])状态：0成功：真x：数组([6.42857143，7.14285714])。

这个解决方案与上一个案例不同。你可以在图表上看到它：

在本例中，最佳解决方案是红色和蓝色约束相交的可行(灰色)区域的紫色顶点。其他顶点(如黄色顶点)的目标函数值较高。

您可以使用SciPy来解决前面部分所述的资源分配问题：

与上一个示例一样，您需要从上面的问题中提取必要的向量和矩阵，将它们作为参数传递给.linprog()，并获得结果：

>；>；obj=[-20，-12，-40，-25]>；>；>；lhs_ineq=[[1，1，1，1]，#人力.[3，2，1，0]，#物料A.[0，1，2，3]]#物料B>；>；>；rhs_ineq=[50，#人力.100，#物料A.90]#物料B&>；>；>；opt=linprog(c=obj，A_uB=lhs_ineq，b_ub=rhs_ineq，.。method="；修订的单工&34；)>；>；>；opt con：Array([]，dtype=Float64)FUN：-1900.0消息：'；优化已成功终止。'；NIT：2 SLACK：Array([0.，40.，0.])。状态：0成功：true x：array([5.，0.，45.，0.])。

结果告诉您，最大利润为1,900，对应于x₁=5和x₃=45。在特定条件下生产第二和第四种产品是无利可图的。您可以在这里得出几个有趣的结论：

第三种产品带来的单位利润最大，所以工厂将生产最多的产品。

第一个松弛为0，这意味着人力(第一)约束的左侧和右侧的值相同。这家工厂每天生产50台，已经满负荷了。

第二个缺口是40个，因为工厂消耗了潜在100个单位中的60个单位的原材料A(第一个产品15个单位，第三个产品45个单位)。

第三个缺口是0，这意味着工厂消耗了全部90个单位的原材料B。这个全部数量被消耗在第三个产品上。这就是为什么工厂根本不能生产第二个或第四个产品，第三个产品的产量不能超过45个单位。它缺少原料B。

opt.status为0，opt.Success为True，表示优化问题用最优可行解成功解决。

SciPy的线性规划功能主要适用于较小的问题。对于更大、更复杂的问题，您可能会发现其他库更适合，原因如下：

SciPy不提供促进模型构建的类或函数。您必须定义数组和矩阵，对于大型问题，这可能是一项乏味且容易出错的任务。

SciPy不允许您直接定义最大化问题。您必须将它们转换为最小化问题。

SciPy不允许您直接使用大于或等于符号来定义约束。您必须使用小于或等于-to。

幸运的是，Python生态系统为线性编程提供了几种替代解决方案，对于较大的问题非常有用。其中之一是纸浆，你将在下一节看到它的作用。

纸浆具有比SciPy更方便的线性规划API。您不必对问题进行数学修改，也不必使用向量和矩阵。一切都更干净，更不容易出错。