两个运动多边形的最大相交时间

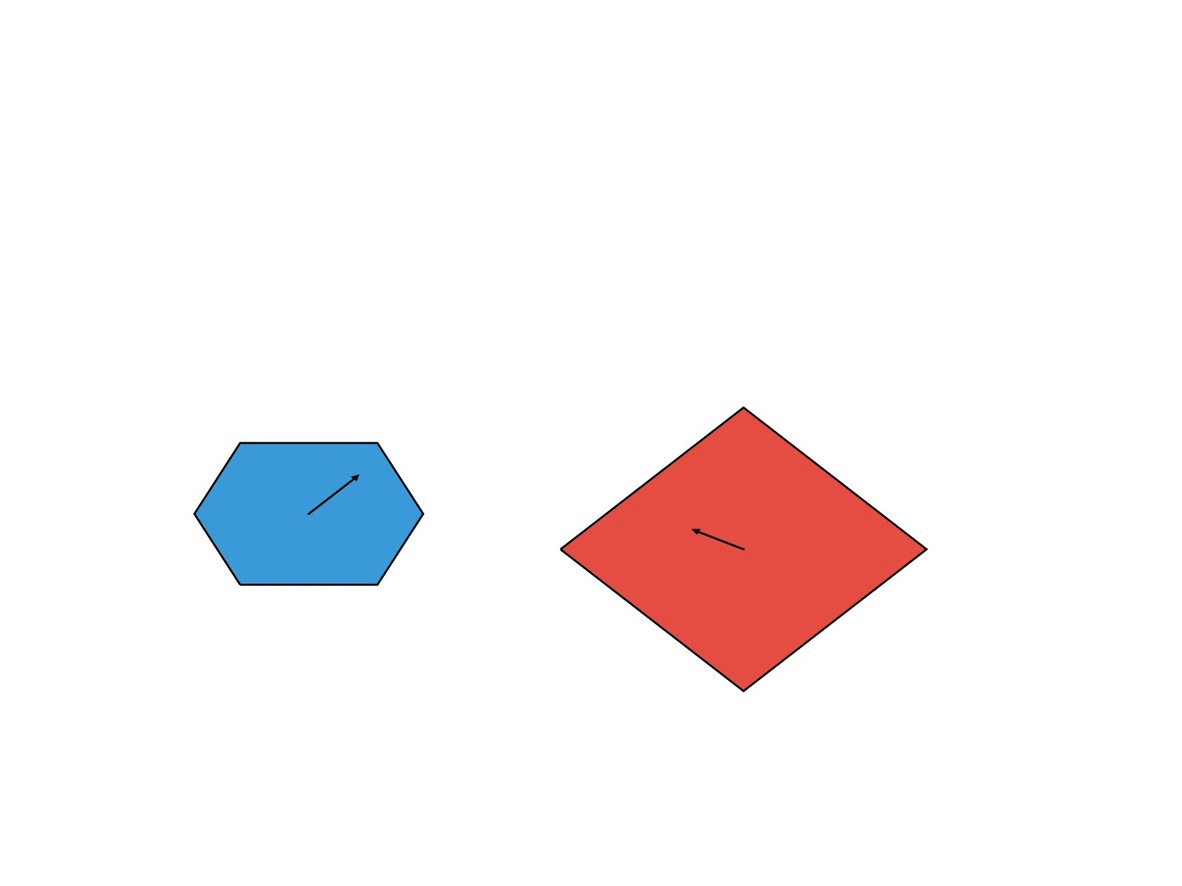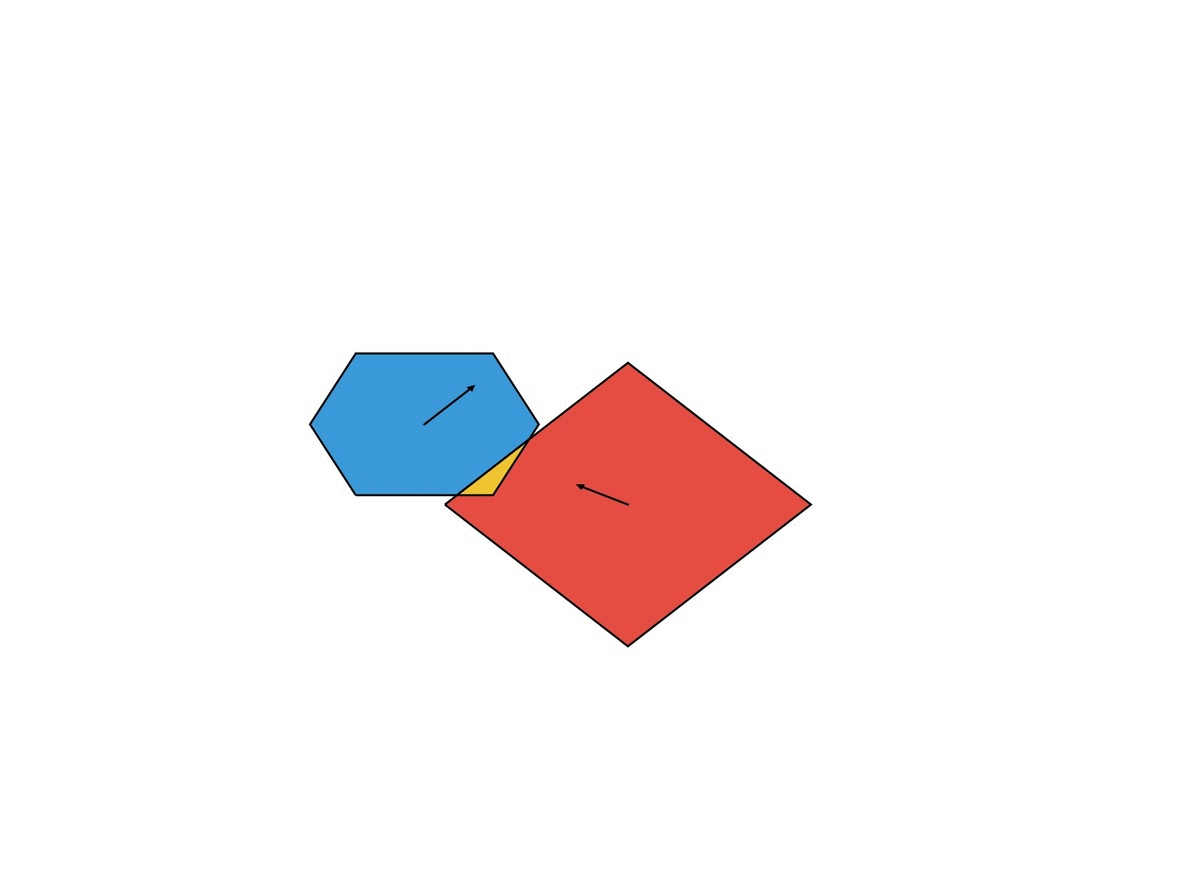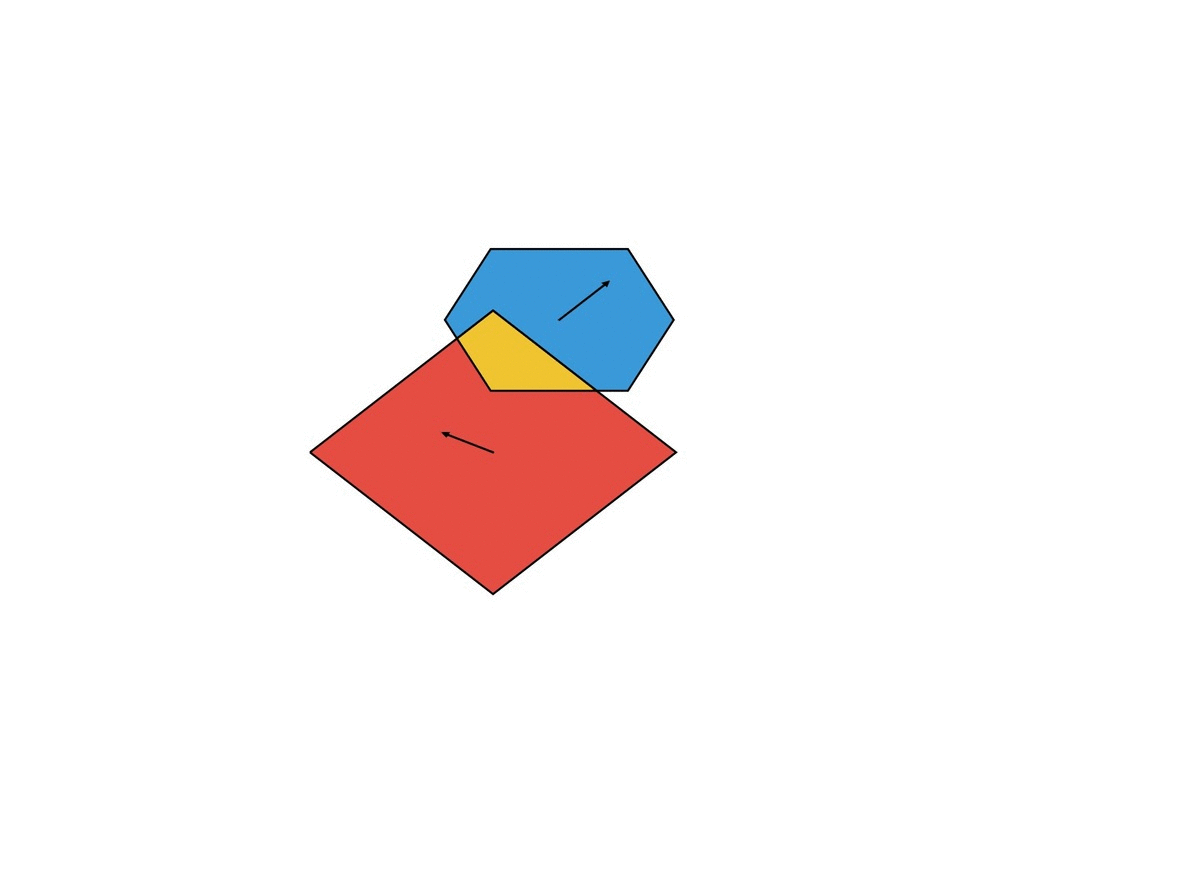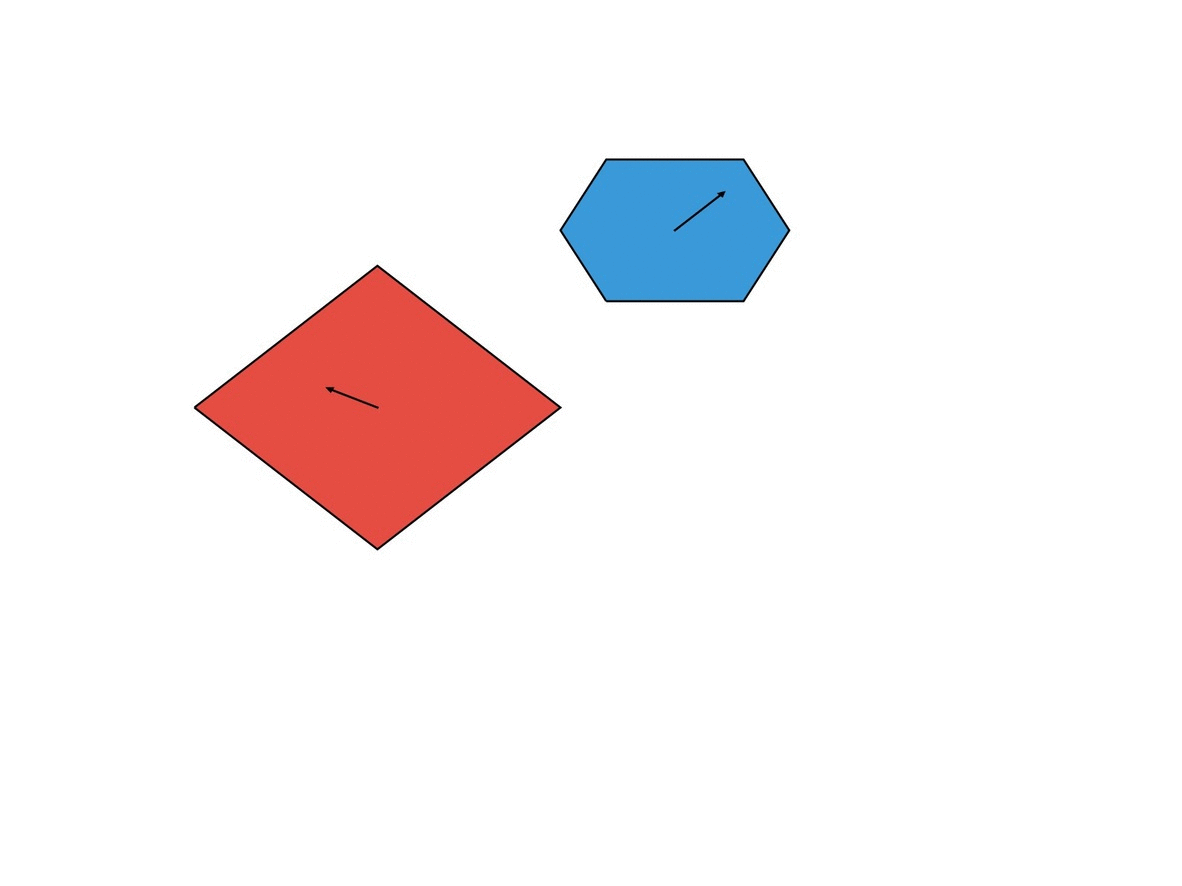
我们有两个凸多边形P和Q，每个都以恒定速度Vp和Vq移动。在某个时间点，它们可能会彼此穿行。我们想找出他们相交面积最大的时间点。这是一幅简单的可视化图，其中黄色区域表示交点，箭头表示多边形的速度。

让我们首先看一下测试两个多边形是否相交的问题。最简单的方法是检查一个多边形的任何边是否与另一个多边形的任何边相交。为此，我们需要一种直线段相交算法。我们可以检查两条直线段A-B和C-D是否相交，如果三角形A，B，C的有符号面积与三角形A，B，D的有符号面积不同，对于C，D，A和C，D，B也是如此。它很简单，运行在O(N^2)内。以下是代码：

将numpy导入为npdef Area(A，B，C)：return np.linalg.norm(np.Cross(B-A，B-C))*0.5def INTERSECT(A，B，C，D)：RETURN AREA(A，B，C)！=Area(A，B，D)and Area(C，D，A)！=Area(C，D，B)def POLYGON_INTERSECT(P，q)：n=len(P)m=len(P)for i in xrange(N)：for j in xrange(M)：IF INTERSECT(P[i]，P[(i+1)%n]，Q[j]，Q[(j+1)%m])：返回True返回False。

还有另一种方法，使用超平面分离定理来实现这一点。我不会解释它，而是画一个例子来说明它是如何在两个维度上工作的，我认为这会更有帮助。取问题中多边形的每条边，并沿其法线方向向外延伸。在下面的绘图中，虚线表示法线和实线，即其中一个多边形的延伸和边缘。让我们称这些边的延伸为“屏障”。现在考虑将这两个形状投影到任何障碍物上。这将使它们变成障碍物上的线段。在相交的情况下，这些线段将在所有障碍物上重叠。查看此图，确认将中心的形状投影到任何障碍物上会产生实线段，而不是两个。

这在没有交叉点的情况下是不同的。在这种情况下，至少存在一个障碍，其中形状的投影不是实线段。在本例中，它是紫色屏障，您可以看到该屏障的法线实际上显示了形状的分隔(紫色虚线)。我们如何检查形状在障碍物上的投影是否相交？我们可以将这些线段再次投影到某条简单的直线上，即水平线，然后看看它们的端点是否重叠。

有了一些快速的多边形求交算法，我们就可以回到原来的问题，在时间上尝试不同的点，检查多边形是否相交。这仍然不是很好，因为不能保证它们会相交，即使这样，我们实际上寻找的是形状相交的时间范围，这样我们就可以计算最大重叠面积。

让我们尝试另一种方法。首先，让我们简化一下，假设其中一个形状是静止的，而另一个形状是相对于它移动的。让我们将移动多边形上的每个点按其速度方向投影出来。

这些光线可能与另一个多边形相交，也可能不相交。在这种情况下，我们有四个交叉点。对于每个交叉点，我们可以根据多边形的速度计算时间。我们可以对这些时间进行排序，并返回最小值和最大值作为重叠的时间范围。

def重叠范围(P，Q，V)：对于zip(*Q.exterior.xy)中的x，y：#将光线模拟为长线段比例=1e10段x=[x，x+scale*V[0]]Segment_y=[y，y+scale*V[1]]line=[Segment_x，Segment_y]Points=交点(P，line)：ix，iy=point.x，point.y#交点时间=。y-iy)/math.supt(V[0]，V[1])interss_times.append(When)interss_times.sorend()if len(Intercluse_Time)==0：打印"；多边形从不重叠"；Elif len(交叉点时间)==1：打印"；接触的多边形不重叠"；返回交叉点时间[0]，交叉点时间[-1]。

在这里，多边形上的每个点创建一条线段，并对照另一个多边形的每条边进行测试。所以我们已经解决了多边形什么时候不相交的问题，但是我们可以用Minkowski几何学做得更好。我们将在两组点之间使用一种叫做Minkowski差的东西。在图像处理中，它与侵蚀有关。这样做的目的是获得一个形状，将其镜像到原点，然后计算镜像的形状和另一个形状的Minkowski和。Minkowski和与膨胀有关，对于两组点P和Q，定义为所有点p+Q，其中p在P中，Q在Q中。

不要太担心两个人的定义。这里是要理解的关键点。我们正在计算这两个多边形是否相交。如果它们相交，则在它们内部的每个多边形中都有一个点。如果是这样，镜像一个多边形并计算Minkowski和多边形将创建一个包含原点的多边形。

下面是计算两个多边形之间的Minkowski差的一些代码。因为这两个集合都是凸的，所以我们取生成的多边形的凸壳来创建一个新的凸多边形。

def Minkowski_Difference(P，Q)：R=[]for i in xrange(len(P))：for j in xrange(len(Q))：R.append((P[i]-q[j]，P[i]-q[j]))返回CONVOX_HULL(R)。

凸壳是包围所有点的最小尺寸的凸多边形。如果你把一串钉子钉在一块木板上，然后在所有的钉子周围拉一个橡皮筋，接触到橡皮筋的钉子就是凸壳。使用Graham扫描可以在O(N*log(N))内计算它。下面的图像显示了两组点(红色和蓝色)及其对应的凸面外壳。它还以黄色显示交点，黄色是多边形和交点中的点的凸包。看到这一点，返回并确认上面的关键点，即如果多边形相交，则它们的Minkowski差包含原点。

现在我们有一个绿色多边形，而不是两个多边形，这是其他两个的Minkowski差。此外，根据Minkowski差的定义，我们知道如果原点在这个多边形内部，则组成多边形的两个多边形彼此相交。这是一个非常重要的事实，让我们可以非常快速地计算碰撞，更重要的是碰撞何时会发生。我们还可以使用从原点沿多边形相对速度方向的一条射线来计算这些多边形的第一个交点和最后一个交点。

下面是正常空间和Minkowski空间中正在发生的事情的说明。您可以看到蓝色和红色多边形相互穿透。同时，您可以看到代表红色和蓝色多边形之间Minkowski差异的绿色多边形同时穿过原点。

一旦我们检索到这个范围(第一个和最后一个交叉点时间)，我们就可以对该范围内的一些点进行采样，并计算重叠部分。两个凸多边形的交集，另一个凸多边形是交点和位于两个多边形内部的点的凸包。使用我们的凸壳函数和相交函数，我们可以计算这个多边形，然后使用测量者的算法来计算面积。

最后，把所有的部分放在一起，我们得到了一个算法，该算法取两个多边形的Minkowski差，然后(通常)计算从原点到Minkowski差多边形的射线的两个交点。利用两个交叉点的时间，我们可以计算作为时间函数的两个多边形的重叠。通过绘制结果，我们得到了这个。

最后的任务仍然是计算该函数的最大值。似乎重叠是单峰的，如果一个形状完全在另一个形状内，则达到最大值。这在本文中是有证据的。由于该函数是单峰函数，我们可以使用三元搜索来快速计算O(LogN)中的最大值。

def findMax(objectiveFunc，LOWER，UPER)：如果abs(上部-下部)<；1e-6：返回(LOWER+UPPER)/2 LOWERThird=(2*LOWER+SUPPER)/3upperThird=(LOWER+2*SUPPER)/3 IF objectiveFunc(LowerThird)<；objectiveFunc(UpperThird)：return findMax(objectiveFunc，lowerThird，UpperThird)否则：返回finfindMax(objectiveFunc，lowerThird，up)。

Minkowski几何学扩展到N维，并且原理保持不变-这使得在更简单的方法不能很好地推广的情况下，在3维中更容易做碰撞检测和响应之类的事情。这个问题是在ICPC ACM世界总决赛上提出的。