深入了解诺伊特定理

最近我们大多数人都躲在家里。上个月，我埋头写了一篇论文，对我在纪念诺特1918年发表关于对称和守恒定律的论文百年纪念大会上的讲话进行了扩展。这让我的禁闭变得容易多了。在花了很长时间研究应用范畴理论之后，回到这种数学物理是件好事。原来我真的很怀念它。

虽然会议上的每个人都在不断强调诺特1918年的论文中有两个大定理，但我的论文只是一个简单的定理-物理学家称之为诺特定理的那个：

人们常常用“对称给出守恒定律”来概括这个定理。这是正确的，但只有在某些假设下才是正确的：例如，运动方程来自拉格朗日。

这就引出了一些有趣的问题。对于哪些类型的物理理论，对称给出了守恒定律？如果我们假设世界是由这类理论描述的，那么我们对世界的假设是什么呢？要弄清这些问题的真相很难，但值得一试。

在许多框架中，我们可以证明与守恒量有关的Noether定理的不同版本。虽然微分几何框架更符合Noether的原始观点，但我的论文没有提到拉格朗日，而是代数地研究了该定理。

…。代数对于几何学家来说，可能就是你所说的浮士德式的报价。如你所知，歌德故事中的浮士德得到了他想要的任何东西(在他的情况下，是一个美丽女人的爱)，魔鬼给了他任何东西，以换取他出卖自己的灵魂。代数是魔鬼给数学家的礼物。魔鬼说：我会给你这台强大的机器，它会回答你喜欢的任何问题。你所需要做的就是把你的灵魂给我：放弃几何，你就会拥有这台神奇的机器。

虽然这有时是正确的，但代数不仅仅是一种计算工具：它允许我们以非常清晰和提炼的方式表达概念。此外，为经典力学开发的几何框架对量子力学来说是不够的。代数方法强调经典力学和量子力学之间的相似性，澄清它们的不同之处。

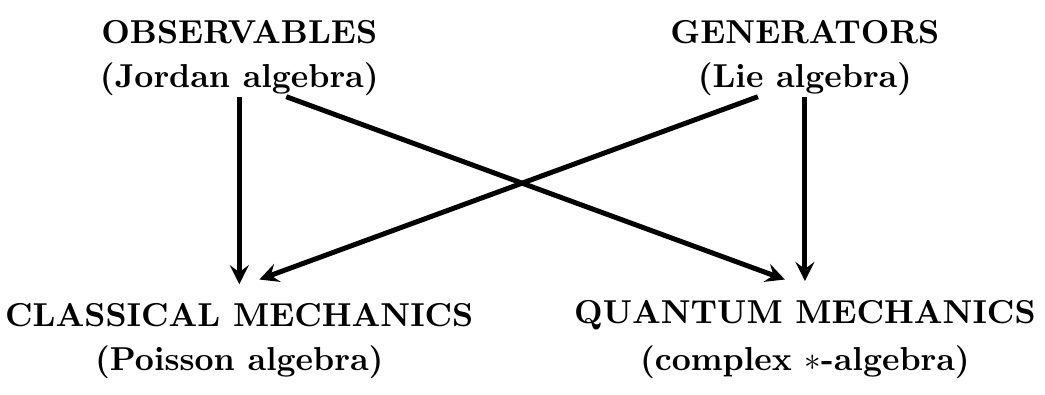
在谈到诺特定理时，我一直使用用来描述物理系统的三个相互关联的重要概念：“状态”、“可观测性”和“产生器”。物理系统具有状态的凸集，其中凸线性组合使我们能够描述状态的概率混合。一个可观测的量是一个实值的量，它的值取决于--可能带有一些随机性--取决于状态。更准确地说：观察值将每个状态映射到实线上的概率度量。另一方面，生成器是产生一组状态的单参数变换的东西--或者对偶地，引起一组可观测的变换。

很容易混淆可观测性和生成器，但我想要区分它们。当我们说‘系统的能量是7焦耳’时，我们把能量当作一个可观测的东西：你可以测量的东西。当我们说“哈密顿量产生时间平移”时，我们把哈密顿量当作一个生成器。

在经典力学和普通复量子力学中，我们通常说哈密顿量就是能量，因为我们有一种方法来识别它们。但是，可观测性和生成器扮演着截然不同的角色-在一些理论中，例如实数或四元数量子力学，它们确实是不同的。在我的论文中考虑的所有理论中，观察到的集合是Jordan代数，而生成元集合是李代数。(别担心，我会解释这些是什么。)。

当我们可以将可观测对象与产生器联系起来时，我们可以将Noether定理表述为以下等价性：