在另一个星球生存的最低定居者数量--科学报告

在另一个星球上生存并自给自足的可行性是什么？这个问题对太空征服的未来特别重要，也许对整个人类的未来也是如此[1，2]。已经提出了使用就地资源和不同的社会组织[3-6，12-19]，但对问题的变量仍然缺乏了解。我在这里展示了一个数学模型可以用来确定在另一个星球上生存的最小定居者数量和生活方式，并以火星为例[6，15]。它是在比较人类为长期生存所需的各种活动的时间要求和定居者的可利用时间的基础上提出的。该模型的一个重要参数称为共享因子，例如，如果活动涉及可由几个人共享的对象的构建，则允许减少每个人的时间要求。为了在火星上生存，对定居者的组织和工程问题做了一些假设[13-15]。计算了定居者的最低人数，结果是110人。可以做出其他假设。提议的方法允许评估和比较，开启了关于最佳生存战略的辩论。如果这个相对较低的数字得到证实，只要定居者的组织合适，在另一个星球上的生存可能比预期的要容易。

人类可能会因为一些灾难性的事件而面临灭绝的威胁1。正如萨根所指出的，在这种情况下，避免我们所知的世界末日的唯一可能的方法可能是在短时间内定居另一个星球2。但是，对于一小部分人来说，在另一个星球上生存的可行性是什么？在足够的遗传多样性和社会适应方面，几位作者3、4、5、6、7已经解决了这个问题。Marin和Beluffi表明，早期的研究过于有限6。他们对不同的多代种群大小进行了模拟，并在统计基础上确定，如果初始大小大于98，人类群体可以合理生存。然而，这个问题并没有从工程能力和长期生存的人力资源方面得到解决。

考虑到时间和有效载荷的限制，可以被送到另一个星球的人数将相当有限。太空X目前正在研究一种巨大的可重复使用的星际飞行器，目标是一次将100人送入这颗红色星球。然而，这是对能力的乐观估计，可重用性的可行性仍然不确定，航天器在火星上着陆和从火星重新发射的资格可能非常困难，需要几十年的时间。在大多数经过充分研究的火星任务方案中，出境旅行和3至6名宇航员的机组人员至少需要6个月的时间，建议使用几枚巨型火箭只向红色行星8、9、10、11运送几十吨的消耗品。而在火星上，许多作者提出了一个基于对12、13、14、15行星大气层或土壤中可找到资源的利用的解决方案。例如，祖布林提议从火星大气中提取二氧化碳，并在12、13、14、15号行星的土壤中找到资源。例如，祖布林建议从火星大气中提取二氧化碳，并在12、13、14、15号行星的土壤中找到资源。例如，祖布林建议从火星大气中提取二氧化碳，并在12、13、14、15号行星的土壤中找到资源。13.即使普遍承认该方法的可行性，但人们对实施的复杂性知之甚少，每年仍需寄送的物品数量仍将是一个巨大的挑战。从实际角度来看，不清楚至少需要多少年才能达到合理的自给自足水平，需要多少火箭才能运送资源和货物，以及在发展期间社会的生活方式和组织方式是什么。如果缓慢的解决过程已经是一个巨大的挑战，如果时间和有效载荷有限，目标是在没有地球人帮助的情况下群体的长期生存，怎么办？

类似的问题也出现在星际旅行中。在O‘Neill、Bond和Martin或Matlof的开创性工作中，已经解决了一小群人的长期生存问题，16、17、18。突出了工程和人为因素问题，特别是系统、知识管理和心理学的可靠性，但可行性仍然不确定，也没有得到很好的理解。本文讨论的一个重要问题是，从人力资源的角度确定最少的个人数量，以及在一个最终可能是人工的外星世界上生存的最合适的组织。在最近的一篇论文中，Hein等人。从国际上重新审视世界船舶问题

只能在给定的一段时间内比较需求和容量。这里建议将行星的轨道周期(OP)作为比较的参考时间。因为许多物体的寿命更长(生命维持系统、居住环境等)。必须使用作业的一部分来考虑它们的维护、维修或重建的时间。如果有可能在地球上找到合适的资源，工作时间要求和工作时间容量取决于：

随着人口的增长，生存的需要也随之增长。然而，由于一些对象可以在几个人之间共享(例如，栖息地或车辆)，工作时间要求的增长速度慢于工作时间容量。因此，预计在最小个体数量以上，约束得到满足，生存成为可能。

表达式的右边部分是工作时间容量。“工作”在这里的定义是广义的，不包括睡觉、吃饭、卫生和休息，但包括养育婴儿、准备食物和社会活动等活动，这些活动对于群体的心理健康和凝聚力都是必要的。可以很容易地提供估计。年累计生存时间由轨道周期乘以个体数量得出。这部分时间用于睡觉(三分之一)，或吃饭、卫生和休息(十二分之一)。此外，儿童和老年人的生产力较低。大约四分之一的人口被认为是非生产性的。总而言之，每年的工作时间容量估计为年生活时间的31.25%。有关详细信息，请参阅方法。

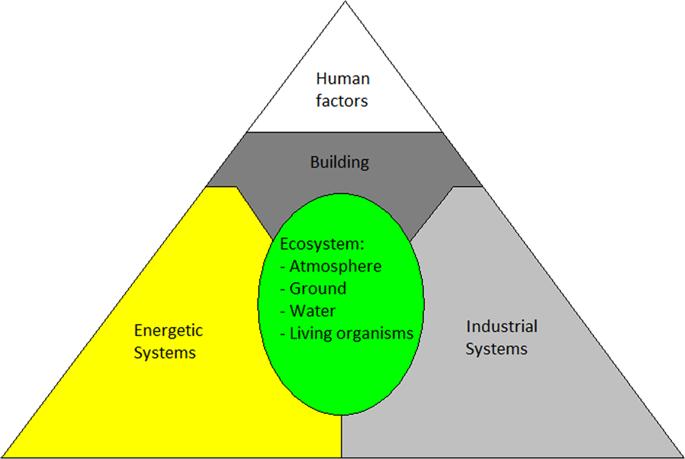
每年的工作时间需求可以通过确定生存所需的所有基本人类活动的集合来估计。显然，为了满足呼吸、饮食或抚养孩子等基本需求，必须实施各种工业流程。例如，建造一座新建筑可能需要开采特定的矿石，并使用铁制的工具，这意味着有一个钢铁工业。对于人数较少的生存，必须将工作时间要求降至最低。因此，有必要最大限度地减少工业的数量，同时利用现代工具最大限度地提高生产率。因此，必须在生产率和工业发展规模较小之间找到一个平衡点。作为解决问题的第一种方法，一种可能的方法是将人类活动分成5个领域，如图1所示：

D1：在生态系统管理领域，主要活动是设计和维护生产适当气体的系统，控制居住模块中的空气成分、压力和温度，收集、生产和回收水，控制所有生物体的生命周期，处理有机废物，种植农业植物，最后生产和储存食物。

D2：在能源生产领域，取决于战略，例如，如果决定使用光伏电池发电和生产汽车用甲烷，主要活动与硅酸盐的提取和加工有关，生产光伏电池、电线，以及通过萨巴蒂尔反应堆提取甲烷。采暖也属于这一类。

D3：在工业领域，特别是冶金和化学领域，主要活动是开采、收集和加工适当的矿石，制造建筑材料，制造物体，以及为其他活动(如农业)生产工具。工业也可能关注玻璃、陶瓷和塑料的生产，以及服装和医药的生产，这取决于生存的战略选择。

D4：构造域。即使在人类到来之前建造了一个基地，它也必须根据定居点的演变(定居者的数量、新的产业、新的工作组织、新的生活方式等)进行频繁的重组。此外，任何建筑的寿命都是有限的。拥有新的生态系统和新的工厂的新的宜居区将不得不建在靠近有趣的当地资源的地方。一切都必须经过设计和组织，以获得良好的生活条件和优化工作。所有与建筑物的建筑、组织(或重组)、维护和建造相关的活动都包括在这里。

D5：最后一个领域涉及社会活动。为了生存和定居点的发展(如果不发展，一个小定居点很容易倒塌)，抚养和教育孩子是很重要的。因此，假设人口增长率为正。其他基本的人类活动涉及医疗保健、做饭、清洁、洗涤、组织工作和决策。为了生存，运动、文化和娱乐的时间可以最小化，但可能不会完全消除。

重要的是，对于每项活动，都必须考虑到一些利润，以应对不可预见的事件。其他活动必须涉及调整进程以适应人口规模以及重组和产业突变的时间。

随着聚落中个人数量的增加，越来越多的物品在他们之间共享。例如，人们可以生活在相同的栖息地，共享相同的空气净化系统、相同的水处理系统、相同的能源生产系统等。如果每个定居者完全隔离，不可能共享，每个人将不得不进行所有活动，总时间需求将乘以个人数量。此外，更多的个人可以通过专业化来提高效率，并可以实施其他行业，从而允许使用更高效的工具。为了兼顾共享的可能性和生产率，可以引入共享因子。给定单个活动的时间要求可以简单地除以这个因子，该因子对于每个活动和每个人的数量都是不同的。可以通过不同的函数(多项式函数、三角函数、阶跃函数等)来估计共享因子。在一定范围内，可以方便地用公式估算。(2)。有关共享系数的详细分析，请参阅方法。

备注：共享系数取决于需求、过程、资源和环境条件，这可能因星球而异。

现在可以获得约束(1)的数学表达式。由于总工作时间容量与个体数量呈线性相关，并且所有活动的总时间需求的计算方法也是n的一个因子，因此方程的两边都可以消去n。

\(r({a}_{j，i})\)是在域\({{\boldbol{d}_{{\boldbol{j}\)中运行活动I的个人年度工作时间要求。

可以估算每项活动的个人年度工作时间要求。因此，共享因子是定义为n(等式)的函数的唯一参数。(2))。因此，生存的最小定居者数量是约束(3)被遵守的最小值n。

即使有足够的个人来生产商品，一个小社会也可能因为许多不同的原因而崩溃。根据Marin和Beluffi的说法，这些原因可能是不育、近亲繁殖、猝死(包括7个遗传问题)、事故或随机事件6.其他具有严重影响的重要风险涉及重要资产的损失、大量资源的损失、不同个人群体之间的致命争斗，或者由于不适当的社会组织而导致的工作效率严重下降(例如，丧失专业知识、丧失动力、官僚作风等)。为了降低风险，一种可能的选择是生产超过最低限度。在和解之初尤其如此，因为任何事故都可能大幅降低产能。在早期阶段，风险的严重程度还取决于初始状态。因此，为了降低风险，重要的是从大量资源和备件开始。需要进行补充性研究，使用不同参数的模拟来评估拟议的最小定居者数量的成功概率。

将该方法应用于火星上的生存。目标是确定与约束(3)相容的最小个体数量。困难在于确定不同参数之间的最佳权衡，特别是要开采的资源类型、要实施的行业、工作组织、生活方式等。火星资源用于生命维持、农业和工业生产的具体利用已经在不同的研讨会上进行了研究，并在报告和书籍12、13、14、15中发表。由于问题的复杂性很高，任何一套选择的可行性和最佳性仍将是不确定的。在火星协会最近组织的一场比赛中，人们被要求定义一个现实的情景来定居这颗红色星球。由于我们的建议是基于保守的假设，以及如果地球人的帮助被停止，仍有生存能力，这里建议将其作为准则15。有关我们的假设的更多详细信息，请参阅方法。

每个人执行每项活动所需的总工作时间已作为个人数量的函数计算出来。根据方程式。(3)只有当工作时间要求小于工作时间容量时，才有可能生存。由于每个人的工作时间要求随着人数的增加而减少(由于共享因素)，因此确定生存所需的最小人数很简单。结果如图2所示。在火星上生存的最低人数是110人。

确定在火星上生存的最小人数。初始人数超过110人的，年工作时间能力大于年工作时间要求。

另一个有趣的结果是，与110个人的个人时间要求相比，一个人的工作时间要求的分布(见图3)。对于一个人来说，问题是要执行所有的工业活动，而对于110个人来说，一半的工作时间是在社会活动领域，包括养育婴儿、保健和文化活动。

以火星为例，已经提出了一种原创性的方法来确定在另一个星球或太空中生存的最小人数。它基于满足所有生存需要所需的工作时间与个人的工作时间能力之间的比较。模型的一个重要参数是共享因子，用于考虑共享和生产率。在为说明该方法而提供的示例中，估计在火星上生存的最小人数为110人。这显然是一个带有众多假设和不确定性的粗略估计。据我们所知，我。

..