球体外翻

拓扑学是研究几何对象不因连续变形而改变的性质的学科。一个标准的低级数学笑话是，拓扑学家认为咖啡杯和甜甜圈相当于一个咖啡杯和一个甜甜圈，因为它们都是Torii-(停顿大笑)-一个可以连续变形成另一个，称为同胚，而不会切割或折痕表面。

在这篇文章中，我们玩一个叫做“外翻”的拓扑游戏。我们的目标很简单：将球体翻转过来，而不切割或折痕。我们考虑球体，尽管环面也是一个有趣的挑战。

斯蒂芬·斯梅尔在1957年证明了球面(具体地说是嵌入三维空间R3\mathbb{R}^3R3中的两个球面S2^2S2)可以反转。然而，这一证明是存在的证明，并没有为那些希望完成这一壮举的人提供特别的指导。

我们应该花一点时间来认识到，类似的在二维内翻圆的问题是不可能的。上图说明，除了引入我们无法消除的循环之外，实际上没有什么可做的。不过，不要相信我的话！外面的经典视频中有一个更复杂的讨论，讨论当我们尝试的时候会发生什么。

自从最初的证明以来，已经发现了许多球面外翻的实现，既有一般性的，也有复杂性的。这篇文章遵循了Bednorz和Bednorz的方法，使用直纹曲面进行解析球外翻。

在走出外翻之前，我们列出了我们的基本规则，其中只有两条：我们不能切割表面，并且表面必须始终保持光滑。请注意，与物理对象不同，允许自交。

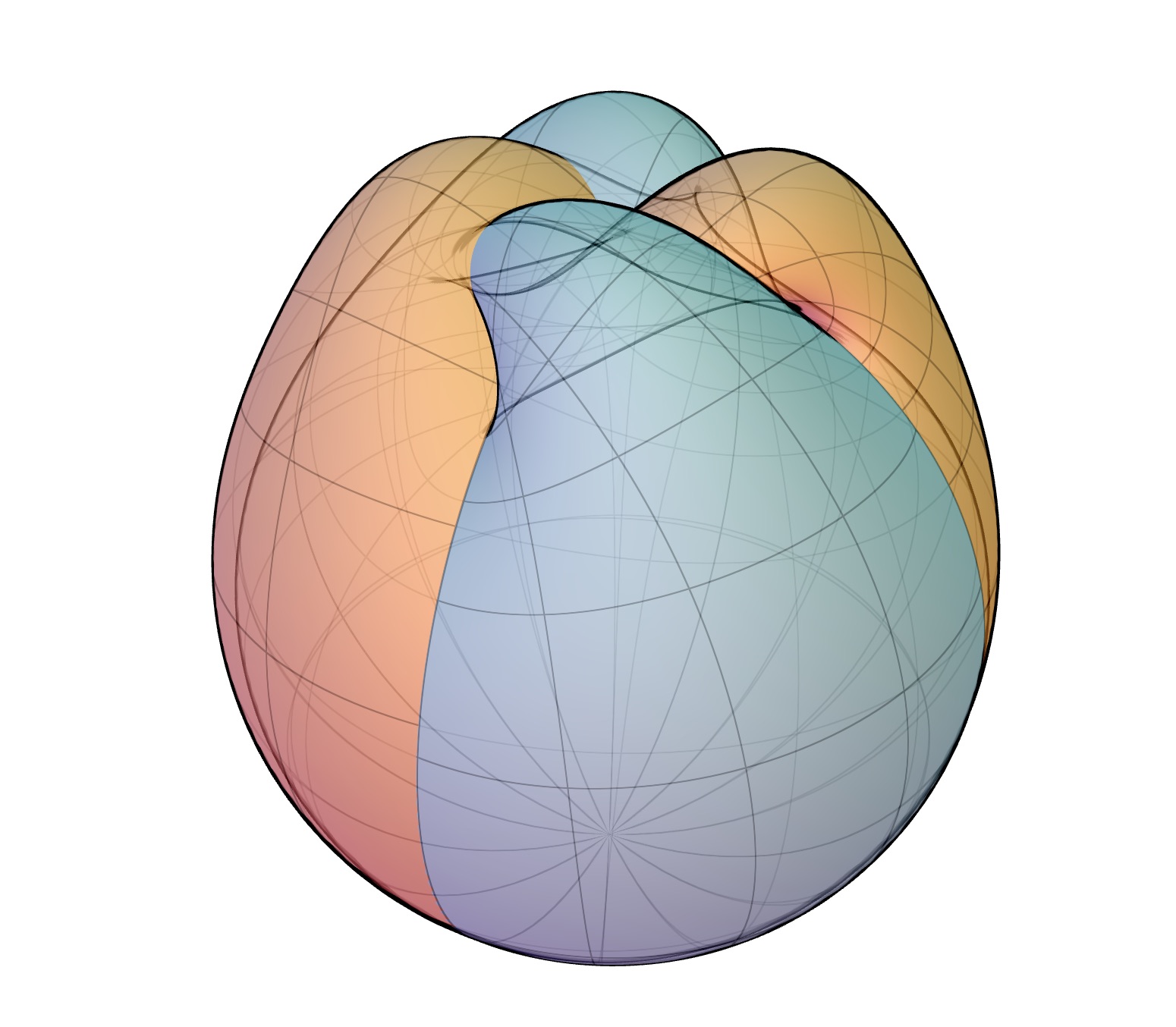
我们从使用直纹面的解析球外翻中完整地介绍Bednorz和Bednorz的球外翻。它过得很快，所以我们会把它分解一下，试着更好地理解它。在此过程中，可以拖动顶部的滑块以检查横截面。

成功！但这一切都发生得非常快。高层发生的事情显然是关键。在某种意义上，我们确实只是简单地将球体的一端穿过另一端，但我们需要一些聪明的技巧来保持顶部的洞平滑。

Bednorz和Bednorz将该方法分解如下。只要球体的两极没有拓扑上有趣的事情发生，我们就可以简单地将它们从方程中去掉，并将焦点放在赤道周围的一个圆柱形频带上。接下来要做的就是小心地操作圆柱形带子，并在过程结束时更换杆子。

他们方法的关键元素是一族直纹曲面，也就是由一条在空间中移动的直线扫出的曲面，它们完成了这一任务。他们提出了一个由时间t参数化的族。他们小心翼翼地证明表面在整个过程中保持光滑，但我们仍将满足于到达目的地，并在沿途目测平滑程度。

x=t cos⁡ϕ+p sin⁡(n−1)ϕ−h sin⁡ϕy=t sin⁡ϕ+p cos⁡(n−1)ϕ+h cos⁡ϕz=h sin⁡nϕ−(t/n)cos⁡nϕ−q th。\BEGIN{ALIGNED}x&；=t\cos\phi+p\sin(n-1)\phi-h\sin\phi\\y&；=t\sin\phi+p\cos(n-1)\phi+h\cos\phi\\z&；=h\sin n\φ-(t/n)\cos n\φ-qth.\end{aligned}x y z​=t cosϕ+p sin(n−1)ϕ−h sinϕ=t sinϕ+p cos(n−1)ϕ+h cosϕ=h sin nϕ−(t/n)cos nϕ−q th.。​变量ϕ\phiϕ将圆柱体的极角从−π-\pi−π参数化为π\piπ，而h将圆柱体的垂直尺寸参数化。它们建议q=2/3q=2/3q=2/3和p=1−|qt|p=1-|qt|p=1−|qt|。

调整时间参数t并观察曲面的形状。有两件特别的事情需要注意。首先，尽管存在自相交，但曲面始终保持平滑；其次，当我们从t=−1移动时，圆柱体边缘的顶部和底部互换位置(稍微旋转一下，这不会给我们带来麻烦)。5t=-1.5t=−1。5到t=1。5t=1.5t=1。5.。

还要注意的是，虽然我们将形象化地看到n=2n=2n=2的情况，但是这种情况也适用于大于2的值。

当然，我们想要的是一个完整的球体，而不仅仅是一个圆柱带，所以他们论文的其余部分集中在使用赤平投影来平滑地闭合圆柱带的盖子，并在整个过程中保持球体的拓扑结构。上面显示了完整的外翻，但现在让我们后退一步，更仔细地关注感兴趣的区域。

就是这样！我很抱歉我对外翻本身没有什么新奇的或细致入微的东西要说，但我在这里的目标是探索视觉呈现，因为视频和图像总是让我希望它更有形一些。

在其他主题中，不乏关于球面外翻的非常好的可视化和资源。下面是一些与此版本和一般主题相关的链接。

这篇文章是使用idyll和regl创建的。你可以在这里找到完整的文章来源。