滥用线性回归立于不败之地

一群人一直给我发来一篇特别草率的文章的链接，这篇文章(错误地)使用线性回归从一些数据中得出了不正确的结论。所以我想我得回到老式的线性回归了，然后稍微谈一下。

如果您有一个数据集合-通常是具有一个自变量和一个因变量的数据(即第一个变量可以随心所欲地变化；更改它将更改第二个变量)，那么您可能对因变量与自变量之间的关系感兴趣。如果你有理由相信它们应该是线性关系，那么你想知道这种线性关系到底是什么。

如果你的数据是完美的，那么你只需要在一个图上画出所有的数据点，自变量在X轴上，因变量在Y轴上，然后你的图就是一条线，你可以得到它的斜率和Y截距，从而完全捕捉到这种关系。

但是数据从来都不是完美的。这其中有很多原因，但没有一组真正收集的数据是完美的。无论真实的潜在线性关系多么完美，真实的测量数据总是会表现出一定的散布。这意味着你可以在收集的数据中画出很多可能的线。它们中哪一个代表最合适的？

因为这是相当抽象的，所以我要谈谈一个例子--这个例子正是用来点燃我对数学的兴趣的！

早在1974年左右，当我还是个二年级的小孩子时，我父亲在RCA工作，作为一名物理学家，参与制造卫星系统的电子产品。对他们正在制造的产品的一个重要要求是它们必须是抗辐射的-这意味着它们可能会暴露在相当多的辐射中，然后才会受到足够的损害而停止工作。

他们的客户--美国国家航空航天局(NASA)、喷气推进实验室(JPL)和美国军方的各种组织--都有非常强烈的要求。对于特定部件的制造设置，他们必须显示故障概况。

他们制造的这些芯片的主要故障模式是电路走线故障。如果能量足够高的伽马射线击中其中一个电路迹线，则该迹线可能会烧毁-中断电路，并导致芯片失效。

他们使用的测试装置有一个伽马射线发射器。因此，他们会进行一次生产运行，从设备中生产一批芯片。然后他们会接受这些，他们会让它们暴露在伽马发射器不断增加的辐射剂量中，并检测到它们何时失败。

对于走线故障，故障概率与芯片暴露的辐射剂量大小成线性关系。因此，为了让客户满意，他们必须向他们展示故障曲线的斜率是多少。“硬辐射”被定义为能够以特定的失败概率持续暴露在一定剂量的辐射下。

所以，我父亲做了一批测试，他有一大堆描述测试结果的小纸条，他需要计算那条线的斜率-这会给出失败的概率是辐射剂量的倍数。

我走进餐厅，他正在那里做这件事，我问他在做什么。所以他向我解释了这件事。就像我刚才解释的那样--除了我爸爸是个比我好得多的老师。我无法像他那样向二、三年级的学生解释这件事！

无论如何，…。我们用来计算最佳直线的方法叫做最小二乘法。它背后的直觉是，您试图找到所有数据点与该线的平均距离最小的线。但简单的平均值并不能很好地发挥作用--因为有些数据点在这条线上方，有些在下方。比方说，仅仅因为一个点比可能的拟合高出100，而另一个点低于100，并不意味着这两个点应该取消。所以你取数据点和线之间的距离，然后把它们平方--使它们都是正数。然后你找到总数最小的那条线--这是最合适的。

例如，这是我半随机生成的数据点的图表。这些点的分布并不是你从真正的观察中得到的，但是它足够好用于演示。

我们这样做的方法是：首先，我们计算和的平均值，我们称之为和。然后使用这些，我们计算斜率为：

在此数据的情况下：我设置了脚本，使坡度约为2.2+/-0.5。图中的斜率为2.54，y截距为18.4。

现在，我们要检查线性关系有多好。有几种不同的方法可以做到这一点。最简单的称为相关系数，或。

如果你看看这个，它实际上是对测量值和期望值(根据回归)之间的变化匹配程度的检查。在顶部，你有一组乘积；在底部，你有相同东西的平方根。从本质上说，底部就是剥离这些标志。最终结果是，如果相关性是完美的-也就是说，如果因变量与自变量线性增加，则相关性将为1。如果相关性变量与因变量相反线性减少，则相关性将为-1。如果没有关系，那么相关性将为0。

对于这组特定的数据，我用一个带有一点随机噪声的线性方程生成了它。相关系数略高于0.95，这完全是你所预期的。

好的，这就是线性回归的基础。让我们回到开始这件事的那篇愚蠢的文章上来。

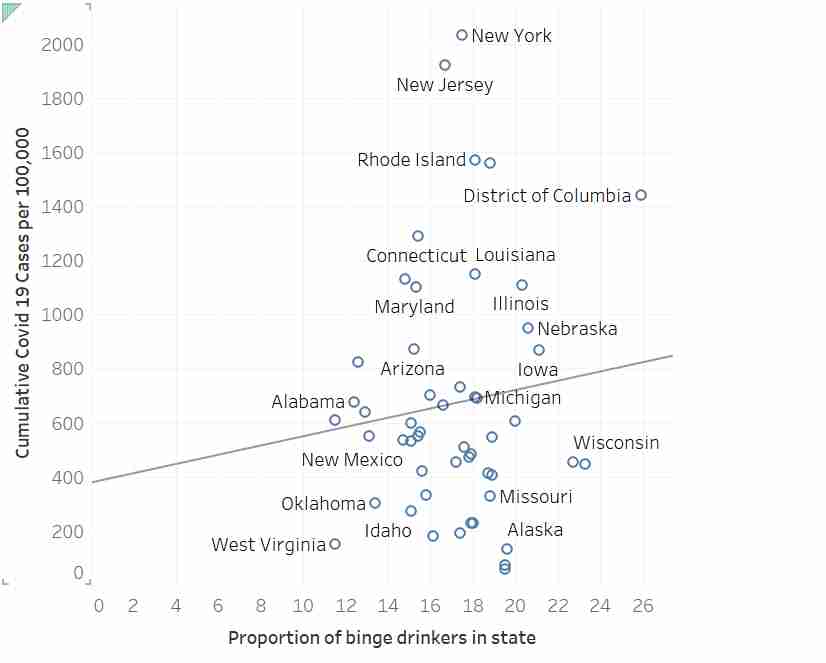
您可以看到这些点的散点图，还可以通过线性回归查看与这些点相匹配的直线。你觉得合身吗？我无法访问原始数据集，因此无法检查它，但我猜测那里的相关性在0.1或0.2左右-也称为“无相关性”。

你看，作者掉进了线性回归的经典陷阱之一。回过头来看看这篇文章的顶部，我是从那里开始解释它的。我说如果你有理由相信线性关系，那么你可以试着找到它。这就是线性回归的巨大诱惑力：无论您输入什么数据，您总会得到一条“最佳匹配”线。如果因变量和自变量没有线性关系-或者根本没有任何实际关系-那么你得到的“最佳匹配”结果就是垃圾。

这就是上图所显示的：您有一个数据点集合，这些数据点对于所有的外观都没有线性关系-而且可能根本没有直接关系。作者正在解释这样一个事实，线性回归给了他一个正斜率的答案，就好像这个正斜率是有意义的一样。但是，只有当真的有一段关系存在时，这才是有意义的。

但当你查看数据时，你看不到线性关系。你看到的是一个相当随机的散点图。在不知道相关系数的情况下，我们不能确定，但在我看来，这条线并不是特别合适。既然作者没有给我们任何证据，除了那条线的存在，就不能相信他们所主张的关系，我们真的没有理由相信他们。他们所做的一切只是证明他们不理解他们正在使用的数学。