自旋电子学研究人员演示如何处理用于数据存储的磁涡

在超快时间尺度上以可重现的方式对磁涡动力学进行电控制是寻求低能耗高效自旋电子器件的关键因素。为了实用，理想情况下，控制方案应该是快速的、可扩展的、非侵入性的，并且能够实现可靠的磁开关。通过外部磁场、自旋极化电流、自旋波或激光脉冲的磁涡旋切换还不能满足这些要求，特别是改变涡旋手性和/或极性的重现性。在这里，我们展示了一种新的封装天米子介导的涡旋切换过程，该过程由简单的皮秒电场脉冲序列通过磁电相互作用驱动。旋涡的手性和极性都表现出明确的反转行为。四种不同磁涡状态之间的明确重复切换为基于非易失性磁涡的信息存储和处理提供了一种节能、高度局部化和相干的控制方法。

磁涡是在微米/亚微米尺度上的圆盘、三角形、正方形和条纹等受限软铁磁结构中形成的。驱动力是受限几何中交换相互作用和形状各向异性之间的微妙竞争。作为拓扑磁缺陷3的一种，磁涡的特征是面内卷曲磁化(手性：顺时针或逆时针)和面外纳米尺寸的磁芯磁化(极性：向上或向下)。磁旋涡具有最简单的拓扑非平凡的自旋构型，表现出几个有利的特征，诸如高热稳定性、可忽略的静磁相互作用、以及用于高密度和非易失性磁存储器和自旋电子器件4、5的多样性信息存储。然而，由于铁磁材料6中磁旋涡的旋转对称性和强的交换相互作用，很难反转磁旋极性和/或手性。已经使用交变磁场7、面内磁场脉冲8、谐振微波脉冲9、场驱动自旋波10、自旋极化电流11、12和光热辅助飞秒激光脉冲激励13来切换涡芯极性。为了解决手性随磁场变化的问题，还引入了破缺对称性结构14。虽然很少有研究考虑涡旋手性和极性的同时控制，但精确地确定磁芯何时发生切换是具有挑战性的，更糟糕的是，顺时针和逆时针方向的涡旋态可能以相似的出现频率随机出现，从而在很大程度上阻碍了可靠的磁涡基自旋电子学的发展。

为了改善这种情况并促进超快全光磁15的涡旋动力学，在这项工作中，我们利用了非共线自旋有序化的另一个特征，即导致自旋驱动的浮现铁电极化P的磁电(ME)效应，它允许外部太赫兹电场E(t，r)通过−E·P与涡旋耦合并驱动该涡旋。这里，ME效应由逆Dzyaloshinskii-Moriya(DM)机制16，17(cf.。另请参阅补充资料中的“磁电相互作用”部分)。ME耦合强度ξm由自旋-轨道相互作用决定，并与外加电场18线性相关。在连续极限下，净铁电极化为P = ξm[(m·∇)m − m(∇·m)]19，20。因此，作用于自旋系统的附加ME驱动有效场为。

$${\mathm{H}}_{{\mathm{me}}{\mathm{=2}}\frac{{\xi_{\mathm{m}{{\Mu_0M_s}}\Left[{{\mathbf{E}}\CDOT\Left({\nabla{\mathbf{m}\Right)-\Left({\nabla\CDOT{\mathbf。Right]+\frac{{\xi_m}}{{\Mu_0M_s}}{\mathbf{m}}\Times\Left({\nabla\Times{\mathbf{E}\Right)。$$。

这里，μ0是真空磁导率，M = M s m，Ms是饱和磁化强度。对于垂直于磁平面的电场(此后由ez方向定义)，Hme中的第一项作为由于界面DM相互作用(DMI)21，22，

$${\mathbf{H}}_{{\mathrm{DM}^{{\mathrm{me}\，{\mathm{=2}}\frac{{\xi_{\mathm{m}{{\mu0m_s}}E_z\Left({\frac{{\部分m_z}}{{\部分{\mathm{x}，\frac{{\部分m_z}}{{\part{\mathm{y}，-\frac{{\Partial m_x}}{{\Partial{\mathm{x}-\frac{{\Partial m_y}}{{\Partial{\mathm{y}\Right)。$$。

进入Hme的最后一项的电场旋度可通过麦克斯韦方程表示为\(\nabla\Times{\mathbf{E=}}-\frac{{\part{\mathbf{B}{{\part t}}=-\mu0\Left({{\mathbf{1}}\，+\，\chi_m^{{\mathm{-1}\右)\frac{{\Partial{\mathbf{M}{{\Partial t}}\)(其中

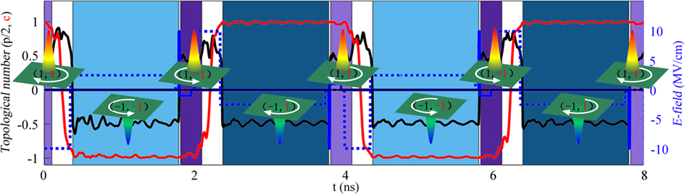
对初始涡旋态施加高斯静电场得到的剩余磁化组态(I-IX)相图。b四个磁涡旋态之间的可重复切换，I → II → III → IV → I……。(由a中的相应辅助颜色标记)、由两个时间不对称脉冲(也称为半周期脉冲，HCP)、E_zp(虚线蓝线)和E_zc(实线蓝线)组成的简单序列。其他剩余的白色区域表示没有明确定义的涡旋态的转变过程。S(黑色实线)和C(红色实线)分别是磁化组态的天子数和手性数。插图：上面的面板显示了所用电场脉冲的衍射限制高斯轮廓空间强度分布；底部面板中的黑色包络显示了实验上可行的强不对称脉冲的一个周期的时间轮廓；蓝色虚线是模拟中使用的数字形状。在这两种情况下，按照麦克斯韦方程的要求，脉冲持续时间上的时间积分为零。

基于Landau-Lifshitz-Gilbert(LLG)方程30利用GPU加速的有限差分微磁模拟来研究涡旋的磁化动力学，

$$\frac{{d{\mathbf{m}{{dt}}=-\frac{\Gamma}{{1+\alpha^2}}\Left({{\mathbf{m}}\次{\mathbf{ef}\right)-\frac{{\alpha\Gamma}}{{1+\alpha^2}}\Left[{{\mathbf{eff}。{m}}\次{\mathbf{H}}_{{\mathm{eff}\right)}\right]，$$。

其中γ为旋磁比，Heff为有效磁场，包括各向同性海森堡交换场、单轴磁晶各向异性场、静磁退磁场和ME场Heff。在本研究中，选择了坡莫合金(Py，一种具有重要技术价值的磁性非常软的材料)在室温下的材料参数：交换常数A = 13 PJ/m，饱和磁化强度Ms = 8 × 105 A/m，磁晶各向异性Ku = 0。吉尔伯特阻尼常数被设置为α = 0.05，其大于大块系统的值，但是对于Py薄膜31在合理范围内。ME耦合强度为ξm = 1·pc/m，这对于在Pt层32、33、34、35、36、37上制备的Py薄膜来说是现实的(详细讨论可以在补充信息中的“磁电相互作用”和“YIG盘的磁涡开关”部分找到)。在典型的Py正方形(宽度99 = nm，厚度3 nm)中，在没有任何外加磁场/电场的情况下，制备了初步稳定的正极性(p = 1)和顺时针手性(c = 1)的磁旋涡。图1中的磁化构形I。(1A)。在模拟过程中，系统由尺寸为(3 nm)3的立方体单元离散。

通过对初始态I依次施加两种不同幅度和脉冲宽度的时间不对称电场脉冲，我们观察到了四个涡旋态之间的超快和高度重复性的转换，如图3所示。1B(比照。另请参阅补充视频S1)。磁芯偏振反转所需的时间约为15 ps，手性反转所需的时间约为325 ps。这些是用于磁涡旋切换的非常高的速度，比由其他控制方案38实现的任何先前报告的速度都要快。此外，切换过程的可靠重复性是一个明显的优势。为了便于实验实现，我们使用麦克斯韦解算器，检查了计算中使用的太赫兹场在样品中的电磁场分布。对于我们的样品的材料、几何形状和大小，以及下面给出的脉冲的强度和持续时间，发现耦合的麦克斯韦-微磁模拟是不必要的，并且下面和补充材料中详述的程序是足够的(参见。“样品中的电场分布”部分和图。补充资料中的S3)。

为了更好地理解，让我们首先细化在时间无关但空间不均匀的电场(即沿z轴施加的静电场的高斯分布)下可能的稳定磁化配置，

$${\mathbf{E}}\Left(\mathbf{r}\Right)=\Left[{0{\mathm{，}}\，0{\mathm{，}}\，E_ze^{-k\Left[{\Left({x-R_{\mathm{x}\Right)^2+\Left({y-R_{\it{y}\Right)^2}\Right]/R^2}。

这里，R = 51 nm，(Rx，Ry)是磁化构型的几何中心，高斯分布的宽度由参数k决定。用E(R)扰动准备的涡旋态i和c = 1，可以用Skyrmion数s和手性数cAs来表征稳定的拓扑磁构型

$$s={\sum\limits_r}\，{\chi_r}\，{\mathm{and}}\，c=\frac{1}{{2\pi}}{\int_0^{2\pi}}{{\mathm{sin}}\Left({\phi-\theta}\right)d\theta}$$。

其中，ϕ = arctan(m y/m x)and\(\chi_{\mathm{r}}=\frac{1}{\mathm{8}}\pi}}[{\mathbf{m}}_{\mathm{r}}\cdot\Left({{\mathbf{m}_{{\mathm{r}}+\widehat{\mathm{x}\，\次。\widehat{\mathm{y}\right)+{\mathbf{m}}_{\mathm{r}}\cot\Left({{\mathbf{m}}_{{\mathm{r}}-\widehat{\mathm{x}\，\time{\mathbf{m}}_{{\mathm{r}}-\widehat{\mathm{y}。例如，具有缠绕数n = 1和核心极化p的旋涡具有半整数Skyrmion数s = Np/2，而理想Skyrmion 39(在r → 0和r → ∞处具有相反的自旋方向)具有整数s = Np。如图3所示。1A，我们更详细地考察了不同高斯电场下初始组态I到剩余态的弛豫。除了四个理想的涡旋态(I-IV)和一个复杂的畸变态IX外，在大而窄的高斯电场存在下，还出现了四个新的包裹式Skyrmion稳定组态(V-VIII)。通过在整个正方形上积分χr，这四种新的、形状良好的构型的Skyrmion数都小于0.5，大部分为~0.3，但如果积分区的半径缩小到相应高斯场的~0.7半宽，则Skyrmion数可能接近±1。从拓扑角度看，这些带有局域拓扑电荷|s| = 1的封装天米子对于s = ±1/2个拓扑扇区之间的切换非常重要，如下图所示，它们确实是在涡旋切换过程中动态发生的，有助于极性和手性反转。

相图通过施加不同的振幅(Ez)和半宽(K)电场提出了以下可能的涡旋转变：(I)从状态I(s = 1/2和c = 1)到IV(s = −1/2和c = 1)的芯极化反转，(Ii)从状态I(s = 1/2和c = 1)到III(s = 1/2和c = −1)的手性反转，和(Iii)从状态I(s = 1/2和c = 1)同时极性和手性反转到状态II(s = −1/2和c = −1)。然而，应该注意的是，动态切换过程是不必要的。相图中的跃迁条件主要由外部参数决定：脉冲幅度和脉冲宽度。

涡核反转过程的磁化动力学细节，包括磁能场的时间演化，如图所示。2A(另见补充视频S2)。我们使用的脉冲一般是可行的。事实上，已经报告了更短和更强脉冲(例如REF)。40)。脉冲由一个强而短的部分(我们称之为头部)和一个长得多、极性相反的弱得多的部分(我们称之为尾部)组成。如参考文献中所示的全部细节。24，只要头部的持续时间短于系统的典型时标(这里是行进周期)，则脉冲的确切形状是次要的。

时间分辨微磁模拟显示了磁化强度和垂直有效磁能场的动态构型。天子数(s，黑色实线)和手性数(c，红色实线)随时间的演化可以有效地描述旋涡切换的动态过程。B涡旋极性的可重复性控制。具有相反核心极化的两个涡旋态(I和IV)被标记为与图中使用的相同的配色方案。1.。

在图3所示的典型情况下。2A，我们观察到当非对称hcp的强(50 mV/cm)和短(15 ps)头部部分(k = 6)到达初始涡旋I时，动态地诱导出具有正核心但负循环的ME场。随着时间的推移，这个有效磁场会颠倒方向，形成一个时间包的天空(Vii)，在大约14 ps(脉冲尾部之前)达到完全形成。最终，封装的Skyrmion衰变为自旋波，在HCP的弱尾部(5 mV/cm)和长尾部(15 0 ps)期间，极性相反的涡旋IV趋于稳定。涡旋IV可以通过遵循非常相似的过程的第二序列(相同类型)脉冲切换回涡旋I，\({\mathrm{IV}}\mathop{\longrightarrow}\limits^{\mathrm{VIII}{\mathrm{I}}\)伴随着自旋波的发射。这些涡旋极性反转显示出非常高和可靠的重复性，如图所示。2B和补充视频S3。显然，潜在的机制不同于通常的旋转性核心激发，在这种情况下，涡核切换动力学涉及到涡旋-反涡旋对的创建和湮灭，并伴随着磁单极子7、8、9、41的注入。这里，拓扑电荷∆s = ±1在两个涡旋态之间的变化是通过i的形成而发生的

如图所示。4B和补充视频S6，我们发现，仅通过略微缩短脉冲持续时间来终止从刺猬天象到涡旋状态III的弛豫(参看)，我们就会发现，仅通过略微缩短脉冲持续时间来终止从刺猬天象到涡旋状态III的弛豫。无花果。3a)，在峰值脉冲后，天米子完全溶解。然而，反转的手性持续到脉冲尾部，并且磁芯也在手性反转后相对较短的时间内反转。涡旋构型II出现，然后通过释放自旋波稳定下来。涡核和手性的同时控制显示出高度可靠的重复性，I → II → I……。(比照。无花果。4B和补充视频S7)。

与图1中的那些相比，HCP相对较短。3用于同时反转涡极性和手性。325ps之前的涡旋动力学与图1中所示相同。 ps之前的涡旋动力学与图1中所示相同。3a，325 ps后的快照中显示了不同的重要行为。b涡旋态I(s = 1/2和c = 1)和涡旋态II(旋涡极性和手性相反，即s = −1/2和c = −1)之间的涡旋转换。

此外，还可以获得两个随机涡旋态之间的独立切换。高效可靠地操纵四种磁涡态。

.