理解并用Python编写JPEG解码器

大家好！JPEGJPEG今天我们要了解👋压缩算法。很多人不知道的一件事是，JPEG不是一种格式，而是一种算法。您看到的JPEG图像大多是内部使用JPEG压缩算法的JFIF格式(JPEG文件交换格式)。在本文结束时，您将更好地理解JPEG算法如何压缩数据，以及如何编写一些自定义Python代码来解压缩数据。在编写解码器时，我们将不会介绍JPEG格式(如逐行扫描)的所有细微差别，而只是介绍基本的基线格式。

既然互联网上已经有数百篇文章了，为什么还要再写一篇关于JPEG的文章呢？通常，当您阅读有关JPEG的文章时，作者只会给出格式的详细信息。您不需要实现任何代码来执行实际的解压缩和解码。即使您确实编写了代码，它也是用C/C++编写的，大多数人都无法访问。我计划通过向您展示一个基本的JPEG解码器如何使用Python3来改变这一点。我将基于这个麻省理工学院许可的代码来实现我的解码器，但为了提高可读性和易解性，我将对其进行大量修改。您可以在我的GitHub资源库中找到本文的修改代码。

让我们从这张由Ange Albertini拍摄的漂亮照片开始吧。它列出了一个简单JPEG文件的所有不同部分。看看这个。我们将探索每一个部分。在阅读本教程时，您可能需要多次参考此图片。

在最基本的级别上，几乎每个二进制文件都包含几个标记(或标头)。你可以把这些标记想像成书签。它们对于理解文件是非常关键的，并且被Find(在Mac/Linux上)这样的程序用来告诉我们关于文件的详细信息。这些标记定义文件中某些特定信息的存储位置。大多数标记后面跟着特定标记段的长度信息。这告诉我们那个特定的段有多长。

我们关心的第一个标记是FF D8。它告诉我们这是图像的开始。如果我们看不到它，我们可以认为这是另一个文件。另一个同样重要的标志是FF D9。它告诉我们，我们已经到达图像文件的末尾。除了FFD0到FFD9和FF01之外，每个标记后面都紧跟一个长度说明符，该说明符将提供该标记线段的长度。对于图像文件开始标记和图像文件结束标记，每个标记的长度始终为两个字节。

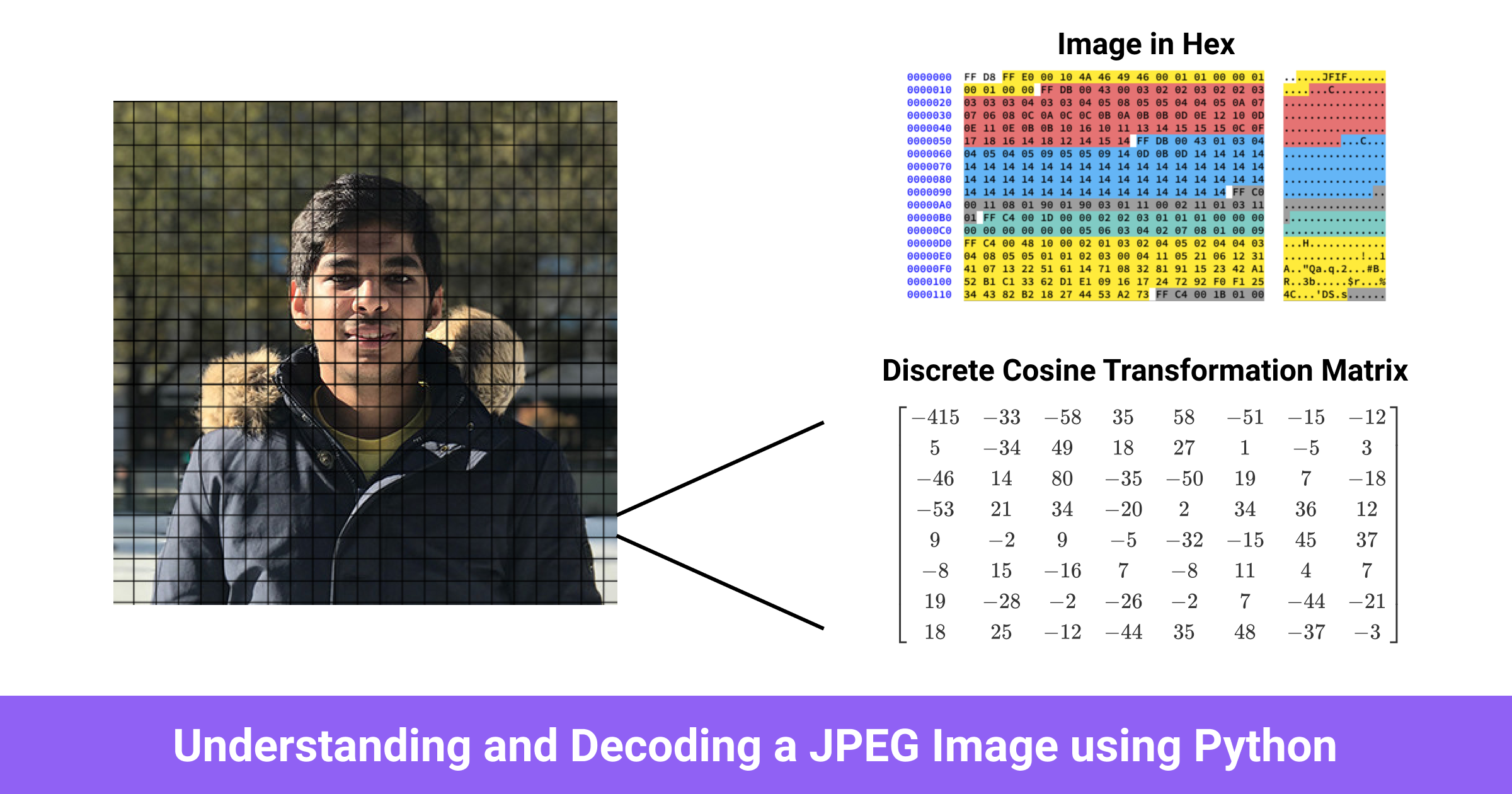
From struct import unPackmark_Mapping={0xffd8："；开始图像"；，0xffe0："；应用程序默认标题"；，0xffdb："；量化表"；，0xffc0："；帧开始"；，0xffc4："；定义霍夫曼表"；，0xffda："；，}class JPEG：def__init__(self，image_file)：with open(image_file，'；rb'；)as f：self.img_data=f.read()def decode(Self)：data=self.img_data While(True)：标记，=解包("；>；H"；，data[0：2])print(mark_mapping.get(Mark))if mark==0xffd8：data=data[2：]elif marker==0xffd9：return Elif marker==0xffda：data=data[-2：]Else：lenchunk，=unpack("；>；H"；，data[2：4])data=data[2+lenchunk：]if len(Data)=0：Break。)img.decode()#输出：#图像开始#应用程序默认标题#量化表格#量化表格#帧开始#霍夫曼表格#扫描开始#图像结束。

我们使用struct来解压图像数据的字节。>；H告诉struct将数据视为大端和无符号短类型。JPEG格式的数据以BIG-Endian格式存储。只有EXIF数据可以采用小端(即使它不常见)。而短码的大小为2，因此我们提供从img_data解包两个字节。你可能会问自己，我们是怎么知道这是短路的。我们知道JPEG中的标记是4个十六进制数字：ffd8。一个十六进制数字等于4位(1个⁄，2个字节)，因此4个十六进制数字将等于2个字节，一个短数字将等于2个字节。

扫描开始部分紧跟在图像扫描数据之后，且该图像扫描数据没有指定的长度。它会一直持续到找到“文件结束”标记为止，所以现在，每当我们看到SOC标记时，我们都会手动“寻找”到EOF标记。

现在我们已经有了基本的框架，让我们继续并弄清楚其余的图像数据包含什么。我们将首先介绍一些必要的理论，然后开始编写代码。

我将首先解释JPEG使用的一些基本概念和编码技术，然后解码自然会与JPEG相反。根据我的经验，直接尝试理解解码有点困难。

尽管下面的图片现在对您没有多大意义，但在我们完成整个编码/解码过程时，它会给您一些可以把握的锚。它显示了JPEG编码过程中涉及的步骤：(SRC)。

假设仅用一个分量编码的图像是灰度数据，其中0为黑色，255为白色。

假设用三个分量编码的图像是编码为YCbCr的RGB数据，除非图像包含6.5.3中指定的APP14标记段，在这种情况下，根据APP14标记段的应用数据将颜色编码视为RGB或YCbCr。RGB和YCbCr之间的关系如Rec中规定的那样定义。国际电信联盟-T T.871|国际标准化组织/国际电工委员会10918-5。

假设用四个分量编码的图像是CMYK，其中(0，0，0，0)表示白色，除非图像包含6.5.3中指定的APP14标记段，在这种情况下，根据APP14标记段的应用数据，颜色编码被认为是CMYK或YCCK。CMYK和YCCK之间的关系如第7条所规定。

大多数JPEG算法实现使用亮度和色度(YUV编码)而不是RGB。这在JPEG中非常有用，因为人眼很难看到小区域内的高频亮度变化，所以我们可以从本质上减少频率，而人眼将无法区分。结果呢？高度压缩的图像，几乎没有明显的质量下降。

就像RGB颜色空间中的每个像素由3个字节的颜色数据(红、绿、蓝)组成一样，YUV中的每个像素也使用3个字节，但每个字节表示的内容略有不同。Y分量确定颜色的亮度(也称为亮度或亮度)，而U和V分量确定颜色(也称为色度)。U分量是指蓝色的量，V分量是指红色的量。

这种彩色格式是在彩色电视还不是很普遍的时候发明的，工程师们想要对彩色电视和黑白电视都使用一种图像编码格式。如果没有彩色电视，YUV可以安全地显示在黑白电视上。你可以在维基百科上阅读更多关于它的历史。

JPEG将图像转换为8x8个像素块(称为MCU或最小编码单元)，更改像素值的范围以使其以0为中心，然后对每个块应用离散余弦变换，然后使用量化来压缩生成的块。让我们对所有这些术语的含义有一个更高层次的理解。

离散余弦变换是一种将离散数据点转换为余弦波组合的方法。花时间将一幅图像转换成一串余弦似乎是无用的，但一旦我们理解了DCT并结合下一步的工作原理，它就有意义了。在JPEG中，DCT将获取一个8x8图像块，并告诉我们如何使用8x8余弦函数矩阵来再现它。单击此处阅读更多内容)。

我们将DCT分别应用于像素的每个分量。应用DCT的输出是一个8x8系数矩阵，它告诉我们每个余弦函数(总共64个函数)对8x8输入矩阵有多少贡献。DCT的系数矩阵通常在系数矩阵的左上角包含较大的值，在右下角包含较小的值。左上角表示频率最低的余弦函数，右下角表示频率最高的余弦函数。

这告诉我们，大多数图像包含大量的低频信息和少量的高频信息。如果我们将每个DCT矩阵的右下角分量设置为0，结果图像看起来仍然是一样的，因为正如我所提到的，人类不善于观察高频变化。这正是我们下一步要做的。

我找到了一个关于这个话题的精彩视频。如果DCT没有太多意义，请注意。

我们都听说过JPEG是一种有损压缩算法，但是到目前为止我们还没有做任何有损的事情。我们只将8x8的YUV分量块转换成8x8的余弦函数块，而不会丢失信息。有损部分出现在量化步骤中。

量化是一个过程，在这个过程中，我们在一个特定的范围内取几个值，并将它们变成一个离散值。对于我们的例子，这只是一个将DCT输出矩阵中的较高频率系数转换为0的花哨名称。当您使用JPEG保存图像时，大多数图像编辑程序会询问您需要多少压缩。您在那里提供的百分比会影响应用多少量化以及丢失多少高频信息。这是应用有损压缩的地方。一旦丢失了高频信息，就不能从生成的JPEG图像中重新创建完全相同的原始图像。

根据所需的压缩级别，可以使用一些常见的量化矩阵(有趣的事实是：大多数供应商都拥有构建量化表的专利)。我们将DCT系数矩阵与量化矩阵进行元素划分，将结果舍入为整数，得到量化矩阵。让我们来看一个例子。

尽管人类看不到高频信息，但如果从8x8图像块中删除太多信息，整个图像看起来就会出现块状。在该量化矩阵中，第一个值称为直流值，其余值为交流值。如果我们从所有量化矩阵中提取DC值并生成一个新图像，我们基本上会得到原始图像的1/8分辨率的缩略图。

同样重要的是要注意，因为我们在解码时应用量化，所以我们必须确保颜色落在[0,255]范围内。如果它们落在这个范围之外，我们将不得不手动将它们夹在这个范围内。

这种编码是优选的，因为大多数低频(最重要的)信息在量化之后存储在矩阵的开始处，而Z字形编码存储在1D矩阵的开始处的所有信息。这对于下一步进行的压缩很有用。

游程编码用于压缩重复数据。在Z字形编码的末尾，我们看到大多数Z字形编码的1D数组的末尾都有这么多0。游程编码允许我们回收所有浪费的空间，并且使用更少的字节来表示所有的0。假设您有如下数据：

增量编码是一种用于表示一个字节相对于它之前的字节的技术。举个例子会更容易理解这一点。假设您有以下数据：

在JPEG中，DCT系数矩阵中的每个DC值相对于其前面的DC值进行增量编码。这意味着，如果您更改图像的第一个DCT系数，整个图像将会出错，但如果您修改最后一个DCT矩阵的第一个值，则只会影响图像的一小部分。这很有用，因为图像中的第一个DC值通常是变化最大的，通过应用Delta编码，我们可以使其余的DC值接近0，从而在下一步的霍夫曼编码中获得更好的压缩效果。

霍夫曼编码是一种对信息进行无损压缩的方法。赫夫曼曾经问过自己，“我可以用来存储任意一段文本的最小位数是多少？”这种编码格式就是他的答案。假设您必须存储以下文本：

这是基于ASCII到二进制的映射。但是如果我们能想出一个定制的地图呢？

这一切都很好，但是如果我们想要占用更少的空间呢？如果我们能够做这样的事情会怎么样：

霍夫曼编码允许我们使用这种可变长度映射。它获取一些输入数据，将最频繁的字符映射到较小的位模式，将最不频繁的字符映射到较大的位模式，最后将映射组织成二叉树。在JPEG中，我们使用霍夫曼编码来存储DCT(离散余弦变换)信息。还记得我告诉过您，对DC值使用增量编码有助于霍夫曼编码吗？我希望你现在能明白为什么。在增量编码之后，我们要映射的“字符”更少，我们的哈夫曼树的总大小也减小了。

Tom Scott有一个很棒的视频，里面有关于哈夫曼编码一般工作原理的动画。在继续之前一定要看一看。

JPEG包含最多4个霍夫曼表格，这些表格存储在“定义霍夫曼表格”部分(从0xffc4开始)。DCT系数存储在两个不同的霍夫曼表中。一个仅包含来自锯齿形表格的直流值，而另一个包含来自锯齿形表格的交流值。这意味着在解码时，我们必须合并来自两个独立矩阵的直流值和交流值。亮度和色度通道的DCT信息是分开存储的，因此我们有2组DC和2组AC信息，总共有4个霍夫曼表。

在灰度图像中，我们只有2张霍夫曼工作台(1张用于直流，1张用于交流)，因为我们不关心颜色。正如您已经可以想象的那样，2个图像可以有非常不同的霍夫曼表，因此将这些表存储在每个JPEG中是很重要的。

所以我们知道JPEG图像包含的基本细节。让我们从解码开始吧！

使用DCT系数组合余弦波并为每个8x8块重新生成像素值

我们将使用基线压缩，根据标准，基线将包含紧挨着的8x8块系列。其他压缩格式的数据布局略有不同。仅供参考，我已经在我们正在使用的图像的十六进制内容中给不同的部分着色。它看起来是这样的：

我们已经知道JPEG包含4张霍夫曼表。这是编码过程的最后一步，因此应该是解码过程的第一步。每个分布式哈希表部分包含以下信息：

位0..3：超线程数量(0..3，否则出错)位4：超线程类型，0=DC表，1=AC表位5..7：未使用，必须为0。

代码长度为1..16的符号数，这些字节的总和(N)是代码的总数，必须为<；=256。

按代码长度递增顺序包含符号的表(n=代码总数)。

它将大致存储在JFIF文件中(它们将以二进制形式存储。我使用ASCII只是为了说明)：

0 1 5 1 1 1 0 0 0 000 a b c d e f g h i j k l。

0表示没有长度为1.1的霍夫曼码，1表示有1个长度为2的霍夫曼码，依此类推。DHT部分中始终有16字节的长度数据紧跟在类别和ID信息之后。让我们编写一些代码来提取DHT中的长度和元素。

JPEG类：#.。def decdeHuffman(self，data)：Offset=0 Header，=Unpack("；B"；，data[Offset：Offset+1])Offset+=1#提取包含长度的16个字节data Length=Unpack("；BBBBBBBBBBBBBBBBB"；，Data[Offset：Offset+16])Offset+=16#提取长度为i的前16个字节元素=[]之后的元素：Elements+=(un.。，Header)打印("；长度："；，长度)打印("；元素："；，len(元素))data=data[Offset：]def decode(Self)：data=self.img_data While(True)：#-Else：LEN_CHUNCK，=UNPACK("；>；H"；，data[2：4])len_chunk+=2 chunk=data[4：len_chunk]if mark==0xffc4：self.decdeHuffman(Chunk)data=data[len_chunk：]if len(Data)==0：Break。

图像起始应用默认表头量化表量化表帧起始Huffman表头：0长度：(0，2，2，3，1，1，1，1，1，1，0，0，0，0，0，0，0，0，0，0)元素：10Huffman表头：16长度：(0，2，1，3，2，4，5，2，4，4，3，4，4，8，5，5，5，5，1。0)元素：8Huffman表头：17长度：(0，2，2，2，2，2，1，3，3，1，7，4，2，3，0，0)元素：34图像扫描结束开始。

甜!。我们得到了长度和元素。现在，我们需要创建一个自定义的Huffman表类，以便可以根据这些元素和长度重新创建一棵二叉树。我厚颜无耻地从这里复制这段代码：

class HuffmanTable：def__init__(Self)：self.root=[]self.element=[]def BitsFromLengths(self，root，element，pos)：if isinstance(root，list)：if pos==0：if len(Root)<；2：root.append(Element)[0，1]中的i返回True返回False：if len(Root)==i：root.append([])if self.BitsFromLengths(root[i]，element，pos-1)==True：返回True返回False def GetHuffmanBits(self，Length，Elements)：self.element=range中i的元素II=0(len(Length))：for j in range(len(Length))：for j in range。list)：r=r[st.GetBit()]return r def GetCode(self，st)：While(True)：res=self.Find(St)if res==0：return 0 elf(res！=-1)：return res class JPEG：#-def decdeHuffman(self，data)：#-hf=HuffmanTable()hf.GetHuffmanBits(Length，Elements)data=data。

GetHuffmanBits接受长度和元素，迭代所有元素并将它们放入根列表中。此列表包含嵌套列表，并表示二叉树。您可以在线阅读霍夫曼树是如何工作的，以及如何用Python创建您自己的霍夫曼树数据结构。对于我们的第一个分布式哈希表(使用我在本教程开始时链接的图像)，我们有以下数据、长度和元素：

十六进制数据：00 02 02 03 01 01 00 00 00长度：(0，2，2，3，1，1，1，0，0，0，0，0，0，0，0，0)元素：[5，6，3，4，2，7，8，1，0，9]。

HuffmanTable还包含GetCode方法，该方法为我们遍历树，并使用Huffman表返回解码的比特。此方法需要比特流作为输入。比特流就是数据的二进制表示形式。例如，ABC的典型位流将是011000010110001001100011。我们首先将每个字符转换为其ASCII码，然后将该ASCII码转换为二进制。让我们创建一个自定义类，它将允许我们将字符串转换为位并逐个读取位。以下是我们将如何实施它：

类流：def__init__(self，data)：self.data=data self.pos=0 def GetBit(Self)：B=self.data[self.pos>；>；3]s=7-(self.pos&；0x7)self.pos+=1 return(b>；>；s)&；1 def GetBitN(self，l)：val

我们在初始化该类时提供一些二进制数据，然后使用GetBit和GetBitN方法读取它。

位0..3：Qt(0..3，否则出错)位4..7：Qt精度，0=8位，否则为16位。

根据JPEG标准，在JPEG图像中有2个默认量化表。一个用于亮度，一个用于色度。这些表从0xffdb标记开始。在。

.