原子化鱿鱼中电流的量子干涉

电流量子干涉是传统超导量子干涉器件(SQUID)中最重要、最广为人知的量子现象。在这里，我们报道了在原子鱿鱼中观察到电流的量子干涉。与传统的SQUID类似，原子SQUID中流经两个结点的电流由于旋转的相位差而受到干扰。这种干扰会导致临界电流的调制。这种调制被观察到三个不同的半径，具有清晰的调制周期，被测量为与基本旋转率一致。这一观察结果表明，用原子电子鱿鱼研究各种有趣的鱿鱼物理是可能的，特别是，有电流的宏观量子现象可以用原子电子鱿鱼实现旋转传感量子测量的目标。

具有约瑟夫森结的回路中的超流体由于其独特的量子现象及其在量子传感和信息处理中的应用，在过去的几十年里得到了广泛的研究。电流的量子干涉是这类系统中最重要的量子现象之一，超导量子干涉器件(SQUID)就是以此命名的。在传统的SQUID中，由于外加磁场，超导体中的电子会受到相位扭曲的影响，而量子干扰引起的临界电流的周期性调制导致了直流SQUID作为最灵敏的磁力计3、4的发展。利用超流氦的中性原子，已经证明了由器件的物理旋转引起的相位扭曲会产生电流的量子干涉，从而使旋转传感成为可能5、6。此外，原子子型SQUID 7、8，一种原子子式的9模拟磁力仪。已经被开发用来探索具有稀薄量子气体的鱿鱼的量子现象。

原子鱿鱼由一个环形陷阱和充当约瑟夫森结的隧道势垒组成。与传统的SQUID类似，可以使用不同数量的约瑟夫森结来制作原子SQID，以满足不同的应用。对于单结原子SQUID，已经观察到相位滑移7和滞后10，表现出与射频(RF)SQUID相似的特性。在双结原子SQUID中，约瑟夫森效应8和阻性流11已经被证实，但至今还没有观察到电流的量子干涉。

在这里，我们通过测量临界电流的周期调制，首次观测到原子SQUID中电流的量子干涉。与DC SQUID类似，外部旋转产生的相位扭曲由于量子干扰而产生对临界电流的周期性调制。我们观察到一个临界原子数的周期调制，这相当于对临界电流的调制，对于三个不同的原子SQUID半径，我们选择这三个不同的原子来演示调制周期的变化。理论上，调制周期等于一个单位缠绕数的环内循环原子的自转速率，可称为基本自转速率Ω0 12。实测的调制周期与直接测量的Ω0一致，证实了观测到的周期调制是旋转诱导量子干涉的结果。这种直流原子鱿鱼的实现使得制造灵敏和紧凑的旋转传感器成为可能。此外，传统SQUID的许多有趣的量子现象都可以用稀薄的量子气体来研究。特别地，可以通过控制物理旋转来操纵电流的量子态，使得能够为许多有趣的应用创建宏观量子态，包括旋转传感13、14、15、16和量子信息处理17的量子计量。

临界电流的周期性调制可以通过计算基于量子相控约瑟夫森结电流和环形陷阱几何形状的原子电子SQUID模型中的总电流来理解(图1a)。总电流是两个约瑟夫森结电流的量子干涉的结果，由下式给出。

其中Ic是原子的临界电流，It是总电流，Ij是原子电子鱿鱼周围的循环电流。由于描述原子的波函数的环形几何和单值性，相位应满足。

式中\(\ω=\frac{\omega}{{\omega}_{0}}\)，其中Ω是原子的旋转速率，n是整数。原子的自转速度可以表示为。

其中\({\omega}_{\rm{ext}}=\frac{{\omega}_{\rm{ext}{{\omega}_{0}}\)，Ωext是原子鱿鱼的外转速，\(\beta_{{\mathm{ATOM}=\frac{{2\pi_{\rm{c}

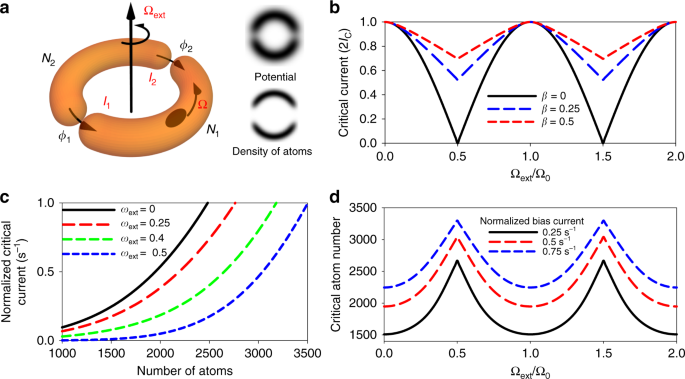
双结原子鱿鱼的示意图。原子化SQUID是通过扫描单束834 nm激光束产生的，束腰为1.7 µm，势垒半高宽为2.1 µm，ΩEXT为原子化SQUID的旋转率，Ω为原子的旋转率。∅1和∅2是约瑟夫森结的相位差，I1和I2是约瑟夫森结电流，N1和N2是每一半的原子数。箭头表示交汇点的移动。计算了半径为3.85 µmb的原子SQUID电势和原子密度，它们是不同Ω原子值下计算的ΩEXT/β0的函数。C归一化临界电流(2Ic/N)，其中Ic是临界电流，N是原子总数，对于半径为3.85ωµm的原子SQUID，它是具有不同 EXT的原子数的函数。β原子随原子数和临界电流的变化而变化。对于每个原子数，计算β原子，以求出归一化临界电流的变化。对3种不同归一化偏置电流的临界原子数随ΩEXT/Ω0的D调制(半径为3.85 µm的原子SQUID)。

方程(1)-(4)等价于DC SQUID的方程4，反映了双结原子SQUID和DC SQUID的基本物理基础相同的事实。在β原子 = 0的极限下(例如，当Ic ≈ 0具有更高的势垒高度时)，我们可以解析地计算总电流：It = 2 I Ccos(πωExt)Sin(∅1 − πωExt)。因此，临界电流为|2I CCOS(πωEXT)|，其建立了周期为Ω0的临界电流的清晰调制。对于有限的β原子，我们可以数值计算临界电流，周期调制幅度随着β原子的增加而减小，如图1b所示。

利用图1b中计算的调制，用二维(2D)的Gross-Pitaevskii方程(GPE)8，18计算了原子电子SQUID中临界电流的预期周期调制。图1c显示了归一化临界电流(有关原子电子鱿鱼中约瑟夫森效应的详细信息，请参阅“方法”)，它是归一化为原子数(2Ic/N)的原子临界电流，作为原子数在原子电子鱿鱼不同转速下的函数。对于固定的原子数量，图1c中所示的归一化临界电流随旋转速度调制。然而，由于归一化临界电流对原子数的强烈依赖性，以及难以稳定地产生具有相同原子数的BEC，因此很难在实验上观察到这种调制。因此，我们使用固定的归一化偏置电流，而不是固定的原子数量，这是通过以固定的速度移动约瑟夫森结而产生的。当转速改变时，临界原子数--即在从直流到交流(AC)约瑟夫森效应与所选择的归一化偏置电流的转变处的原子数量--周期性地调制，如图1D的GPE计算所示。我们选择这种临界原子数的调制作为观察电流量子干涉的一种方式。

在先前的工作19中，通过扫描激光束产生的时间平均电位，即绘制电位(详见绘制电位上的“方法”)被用来创建各种原子电路20，并且这里使用该方法来创建双结原子电子鱿鱼，如图1a所示。在扫描过程中，通过降低特定位置的激光束功率来控制原子鱿鱼中障碍物的高度、厚度和位置的变化。

87Rb BEC是在具有不同转速的双结原子鱿鱼中创建的(有关详细信息，请参阅BEC生产中的“方法”)。然后，将两个结彼此移动以产生如图2a所示的归一化偏置电流0.8 s−1，并且将两个结的旋转速率选择为ΩExt + 2πf和ΩExt − 2πf以实现这一点。在这一结移动步骤之后，通过原位吸收成像测量原子数量，以确定归一化布居差\(z=\frac{{N_2-N_1}}{N}\)(见图11a)。Z从DC(由于保持相同密度的原子在结和N >； Nc之间的隧穿而保持恒定的z，其中Nc是临界原子数)到AC(由于原子的净隧穿减少而导致结上的密度差异和N <； Nc)约瑟夫森效应的变化可以在图2b中看到，对于原子的两种不同的旋转速度。为了确定临界原子数，数据用带有斜率的直线和带有过渡点的常数的分段函数拟合。

计算Ω0不是平凡的，因为与陷阱23的半径相比，原子波函数的宽度很重要。计算是通过在旋转坐标系中将BEC的能量最小化来实现的，而GPE是在2D中进行的。图4a显示了Ω0的实测值和计算值的比较。基于Ω0测量数据进行半径估计的最佳拟合值为0.96，正好位于标定尺度的1σ不确定度范围(0.97和1.0 3)之外。这种小位移的一个可能原因是陷阱电位中的小缺陷改变了Ω0的值。这一机制和其他可能的转变机制可能会在未来进一步研究。

曲线图中的误差条代表标准误差。Ω0/2π的实测值和计算值的比较(使用gpe进行计算)。这三条曲线对应于雾化鱿鱼半径的校准刻度。用GPE模拟和DC SQUID理论计算得到的B-d临界原子数随转速的变化，以及测量数据和最佳拟合结果，验证了B-d临界原子数与旋转率的关系。对于b，半径为4.82 µm；对于c，半径为3.85 µm；对于d，半径为2.891 µm。

图3中数据集的调制波形与图1D中的理论曲线相比显示出一些不同。为了更详细地研究这些差异，我们对测量临界原子数的实验序列进行了动态2D GPE模拟。图4b-d显示了数据集和DC SQUID理论曲线的比较。GPE仿真结果与DC SQUID理论在波形上有很好的一致性。然而，临界原子数在这两种计算之间有一个恒定的变化。我们认为这种转变的发生是因为动力学不是完全绝热的。因此，微小的残余相位涨落引发了从直流到交流约瑟夫森效应的转变，净效应是降低临界电流，从而增加临界原子数。GPE模拟结果与实验数据相比仍有一定差异。主要区别在于第二次振荡的振荡幅度降低。这种类阻尼效应可能是由势原子和非旋转热原子的静态微扰引起的。一项改变静态微扰和热原子振幅的专门研究可能会在未来进一步阐明这一效应。

DC SQUID理论与GPE模拟的良好一致性表明，该系统是实现稀量子气体下常规SQUID各种量子现象的理想系统。例如，原子电子鱿鱼提供了通过利用其以高分辨率和灵敏度24检测各种多体状态的能力来研究宏观量子效应的可能性。利用这种独特的能力，有可能模拟和研究常规SQUID的许多量子现象，以解决关于宏观量子态25的性质的各种紧迫的未决问题。另一个有希望的方向在于创造不同角动量状态的宏观叠加。这些状态可与Leggett-Garg不等式26一起用于旋转传感的量子计量、量子信息处理以及宏观现实主义的可能测试。

在前面的工作8中，通过与偏置电流的比较测量临界电流，用原子电子SQUID演示了约瑟夫森效应。结果表明，归一化电流定义为(doz=2i/N)，其中i为原子电流，N为原子总数，(z=frac{{N2-N1}}{N})为归一化布居差，是描述原子鱿鱼约瑟夫森效应18的有效方法。通过以旋转频率f使两个结彼此靠近，可以感应偏置电流。归一化偏置电流可计算为(点z0=4f)，其中z0是相同化学势和原子密度下的平衡归一化布居差。约瑟夫森效应在直流区和交流区是约瑟夫森效应，其中(点z{rm{c}}，&rm{c})是归一化临界电流，在交流区，原子鱿鱼的两个区域之间存在原子密度差.在交流区，当(点zrm{c})是归一化临界电流时，约瑟夫森效应是在交流区，而在交流区，原子鱿鱼的两个区域之间存在着原子密度的差异，当(点zrm{c})是归一化临界电流时，约瑟夫森效应是在交流区，而当(点z{rm{c}})是交流区时，约瑟夫森效应是在交流区，其中是归一化临界电流.。

绘制电位是来自快扫描激光束19的时间平均光学电位。本实验使用了两束绘制光束。一种为垂直涂装光束，波长为834 nm，腰围为1.7 µm；另一种为水平涂装光束，波长为10 6 4 nm，腰围为12 µm，涂装频率分别为15 kHz和33 kHz。垂直光束绘制的雾化鱿鱼的陷阱深度为82 NK，障碍物的全宽最大为