如何从第一原理导出卷积

戴利：你有没有想过卷积有什么特别之处？在这篇文章中，我从第一原理推导出卷积，并证明它自然产生于平移对称。

“肯定的欢爽”原则就像“肯定的欢爽”那样提供便利。(克劳德·阿德里安·赫尔维修斯)。

在我的本科学习期间，我在以色列理工大学攻读电气工程专业，我总是对卷积这样一个重要的概念不知从哪里冒出来感到震惊。这个看似武断的定义就像一粒沙子打乱了原本美好的信号处理世界图景。让卷积从基本原理中出现，而不是假设它，那该有多好！正如我将在这篇文章中说明的那样，这样的首要原则是平移不变性或对称性的概念。

让我从基础信号处理课程中教授的公式开始，该公式定义了两个n维向量x和w的离散卷积[2]：

这里，为方便起见，我假设所有的索引都是从0到n的−1，并且都是模n；可以很方便地将向量看作定义在圆上的向量。将上面的公式写成矩阵-向量乘法会产生一个非常特殊的矩阵，称为循环数：

循环矩阵具有多对角线结构，每条对角线上的元素具有相同的值。它可以通过将向量w[3]的移位(模n)形式堆叠在一起来形成；为此，我使用记号C(W)来表示由向量w形成的循环矩阵。由于任何卷积x∗w都可以等价地表示为乘以循环矩阵C(W)x，因此我将互换使用这两个术语。

我们在线性代数中学到的第一件事就是矩阵乘法是非对易的，即一般说来，AB≠BA。然而，循环矩阵是非常特殊的例外：

或者换句话说，C(W)C(U)=C(U)C(W)。对于任何循环矩阵或u和w的任何选择都是如此。等价地，我们可以说卷积是交换运算，x∗w=w∗x。

W=[0，1，0…]的特殊选择。，0]产生将向量向右移位一个位置的特殊循环矩阵。这个矩阵称为(右)移位运算符[4]，用S表示。右移位运算符的转置是左移位运算符。显然，先左移后右移(或反之亦然)不会做任何事情，这意味着S是正交矩阵：

循环矩阵可以用它们的交换性来刻画。似乎仅显示带移位的交换性就足够了([5]中的引理3.1)：

这个“如果且仅当”语句的第一个方向导致了一个非常重要的属性，称为平移或平移等价[6]：卷积与移位的交换性意味着，无论我们是先移位向量然后卷积，还是先卷积后移位-结果将是相同的。

第二个方向允许我们将卷积定义为移位等变线性运算：为了进行移位交换，矩阵必须具有循环结构。这正是我们从一开始就渴望的，让卷积从平移对称的第一原理中浮现出来[7]。与信号处理书中通常给出卷积的公式并证明其移位等变性质不同，我们可以从移位等变的要求出发，将卷积的公式作为唯一可能的线性运算来满足它。

信号处理课程教授的另一个重要事实是卷积和傅立叶变换之间的联系[8]。同样在这里，傅立叶变换出乎意料地落地，然后显示它对角化卷积运算，允许在频域中执行两个向量的卷积，作为它们的傅立叶变换的元素乘积。没有人解释过这些正弦和余弦是从哪里来的，它们有什么特别之处。

为了弄清真相，回想一下线性代数中的一个事实：

换句话说，满足AB=BA的两个矩阵将具有相同的特征向量(但可能具有不同的特征值)[9]。由于所有循环矩阵都是可交换的，我们可以选择其中一个并计算其特征向量-上述定理确保这些特征向量也将是所有循环矩阵的特征向量。

选择移位算子S很方便，因为S是正交矩阵，我们希望它的特征向量是正交的[10]。一个简单的计算(参见[5]中的第4.1节)可以得出这样的结论

我希望在这一点上，你有你今天的第二个“顿悟”时刻：这就是正弦和余弦的来源！它们是移位操作符的特征向量；我将它们表示为矩阵Φ的列。请注意，特征向量是复数，因此在转置Φ时需要进行复共轭。与Φ*相乘(从左开始)称为傅里叶变换，由Φ乘以傅立叶逆变换。

因为所有的循环矩阵都是联合对角化的，所以它们也通过傅立叶变换对角化[11]。它们只在特征值上有所不同。最后遗漏的一点是意识到。

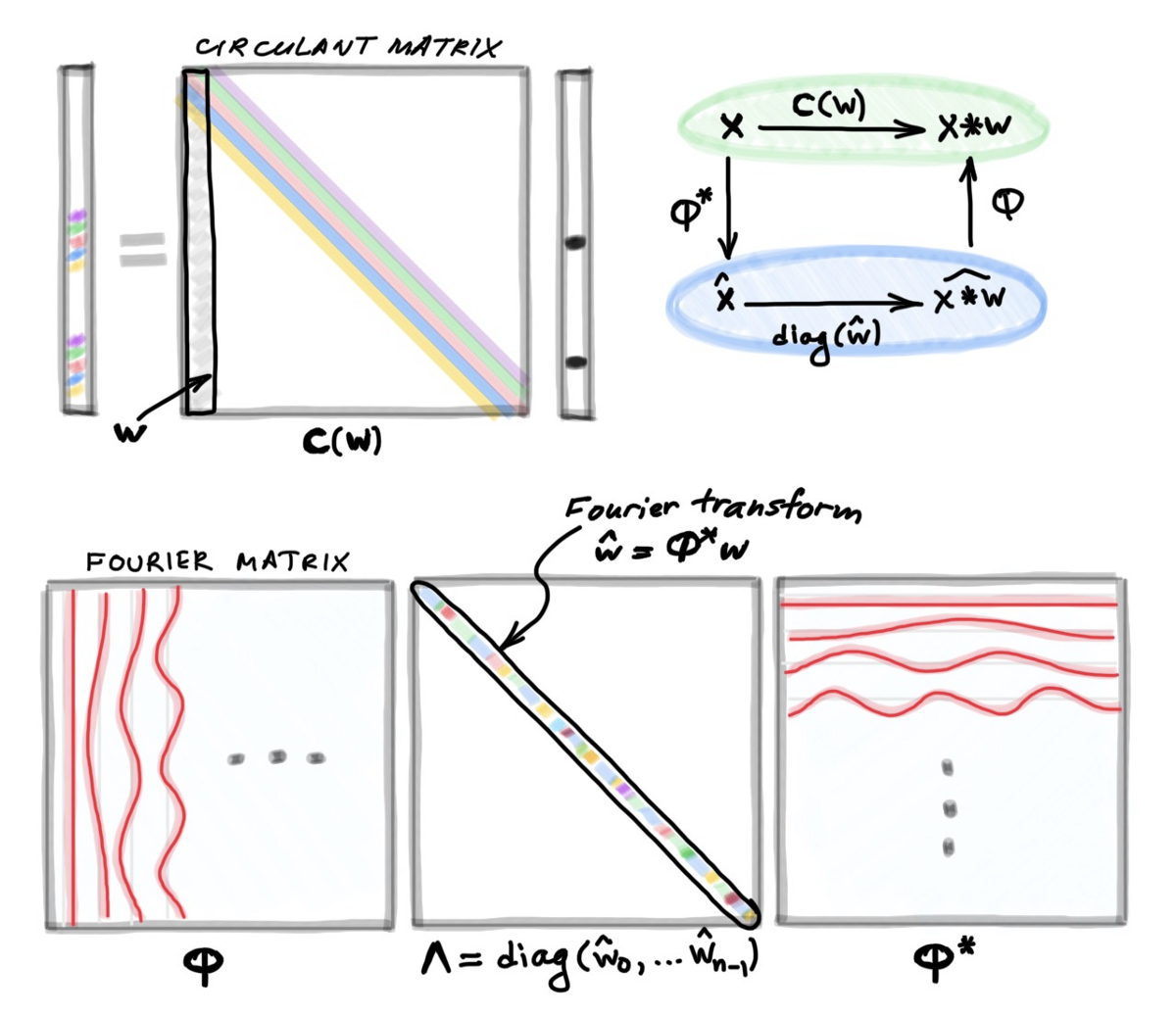
现在我们可以把拼图的所有部分放到一个称为卷积定理的语句中：卷积x∗w可以在原始坐标系(有时称为“空间域”卷积)中作为应用于x的循环矩阵C(W)来计算，也可以在傅立叶基(“谱域”)中通过首先计算Φ*x的傅里叶变换，将其与w[12]的傅立叶变换相乘，然后计算反傅立叶变换来计算。

由于Φ具有特殊的冗余结构，因此乘积Φ*x和Φx可以使用快速傅立叶变换(FFT)算法以𝒪(Nlogn)复杂度计算。

为什么卷积的这样一个定义很重要，应该这样教呢？在这里，我将重复赫尔维修斯的话，我以这样的话开始这篇文章：“对某些原则的了解很容易弥补对某些事实的缺乏”。在卷积的情况下，它是从第一原理推导出来的，很容易推广到其他领域。在下一篇文章中，我将展示如何在图上定义卷积，以便生成图深度学习架构的关键构件。

[1]A.Domquiez-Torres，卷积的历史和起源为卷积运算的概念和符号的历史发展提供了一个引人入胜的旅行。卷积积分第一次出现在J.B.D‘Alembert(1754年)的泰勒定理的推导中，他研究了系统中的重要分点(Sur Différents Points du Système du Monde)。这一优先权经常被错误地归因于P.-S.de Laplace，Mémoire sur l‘Inclinaison Moyenne des Orbites des Comètes，Sur la Figure de la Terre et Sur les Functions(1773年)。Mémoire de l‘Académie Royale des Sciences de Paris，SavantsÉtrangers 7：503-540，虽然这本出版物没有卷积的痕迹。拉普拉斯确实在他后来的回忆录“概率论”中使用了卷积，这本回忆录写于1778年，出版于1781年。早期的命名尝试包括résultante(法语中“Resulant”的意思，查尔斯·卡勒(Charles Cailler)于1899年首次使用)，Composzione(意大利语中“作曲”的意思，维托·沃尔特拉(Vito Volterra)于1910年使用)和Faltung(1923年古斯塔夫·多奇(Gustav Doetsch)在德语中的字面意思是“折叠”)；后者在20世纪初主导了德国文学。英文名字卷积来自拉丁语的con(“一起”)和volvere(“卷起”)，是德语Faltung的直译，俄语的变体свёртка也是如此。英语术语的第一次使用可以追溯到奥雷尔·弗里德里希·温特纳(Aurel Friedrich Wintner)1934年的论文；后来它被Doetsch(1937年)和Gardner and Barnes(1942)的权威作品巩固在文学中。星形符号是沃尔特拉在1910年首次使用的，尽管形式不同。珀西·约翰·丹尼尔用的是点符号。卷积的第一个现代记法是f∗g，它是两者的组合，应归功于doetsch(1923年)。

[3]注意，C(W)的行具有向量w的转置，导致出现在卷积公式中的反射，并将其与相关的相关概念区分开来。注意边界条件(右上角和左下角的C元素)。

[5]B.Bamieh，发现变换：关于循环矩阵、循环卷积和离散傅立叶变换的教程(2018)。1805.05533提供了我在这篇文章中讨论的派生的详细信息。

[6]有些人经常混淆不变性(在拉丁语中的意思是“不变”)和等价性(“以同样的方式改变”)，许多信号处理书籍将我在这里讨论的属性称为“移位不变性”。如果f(Sx)=Sf(X)，则函数是平移等变的。换句话说，我们是否先应用移位，然后应用移位或反之亦然，这并不重要。不同的是，移位不变性是不受移位影响的性质：函数f(Sx)=f(X)是移位不变的。移位不变性是物理学中的一个基本概念(它经常以“平移对称”的名义出现)，它表明物理定律不依赖于空间中的位置。在经典力学的变分公式中，动量守恒定律这样的基本定律是由Noether定理由位移不变性导出的。

[7]等方差的概念更一般，可以用群论形式主义加以推广。这一框架在T.Cohen和M.Wling的Group等变卷积网络(2016)中使用。程序。ICML，将CNN卷积层的移位等价性推广到更一般的运算，如旋转。假设f：X→Y，其中X和Y是一些不同的空间，分别在X和Y的元素上定义了相应的运算组𝒢和𝒢‘，则组等价表示为f(𝔤(X))=𝔤’(f(X))，其中𝔤∈𝒢和𝔤‘∈𝒢’。注意，𝔤‘不一定等于𝔤，因为输出空间Y的结构和偶数维可以不同于输入X的结构和偶数维。本文中讨论的标准卷积是一种特殊情况，其中X=Y是n维向量的空间，𝒢=𝒢’是平移组，而𝔤=𝔤‘是移位运算符。

[8]由于我们处理的是有限维向量，术语“傅立叶变换”在这里指的是离散傅立叶变换(DFT)。

[9]更准确地说，联合对角化意味着两个交换矩阵具有相同的特征空间，因为在一般情况下，特征值可以具有非平凡的重数。因为在我这里讨论的情况下，所有的特征值都很简单，所以我们可以讨论一个共同的特征基。

[10]然而，由于S是非对称的，所以它没有实特征值(对称实矩阵具有实特征值)。S的特征值恰好是单位的复根。

[11]当我说矩阵C被傅立叶变换“对角化”时，我的意思是矩阵Φ*CΦ是对角化的。由于傅立叶变换是正交矩阵(Φ*Φ=i)，因此它在几何上充当相当于n维旋转的坐标系的改变。在这个坐标系中，C的作用变成元素乘积。

[12]在信号处理中，通常在频域中设计滤波器，因此从不显式计算w的傅里叶变换。