森林砍伐与世界人口可持续性：一项定量分析

本文采用统计学的观点，对当前世界人口增长与平行森林砍伐过程的可持续性进行了定量分析。我们考虑了一个基于由连续时间随机游走驱动的随机增长过程的简化模型，该模型描述了人类的技术进化，并结合一个确定性的广义Logistic模型来描述人与森林的相互作用，并评估了避免人类文明自我毁灭的可能性。根据目前的资源消耗率和对技术增长率的最佳估计，我们的研究表明，我们生存下来而不面临灾难性崩溃的可能性非常低，在最乐观的估计中不到10%。

在过去的几十年里，关于气候变化的辩论已经具有了全球重要性，并对国家和全球政策产生了影响。人类活动造成的许多因素被认为可能是造成观察到的变化的原因：其中，水和空气污染(主要是温室效应)和森林砍伐是最主要的原因。虽然人类对温室效应和温度变化的贡献程度仍然是一个讨论的问题，但森林砍伐是一个不可否认的事实。事实上，在人类文明发展之前，我们的星球被6000万平方公里的森林所覆盖1。由于砍伐森林，目前只剩下不到4000万平方公里2。在这篇文章中，我们关注的是滥砍滥伐的后果。

树木为我们的星球提供的服务范围从碳储存、氧气生产到土壤保护和水循环调节，不一而足。它们支持自然和人类的食物系统，并通过建筑材料为包括我们在内的无数物种提供家园。树木和森林是我们最好的大气清洁剂，由于它们在陆地生态系统中扮演着关键角色，如果没有它们，很难想象包括我们在内的许多物种在地球上的生存。从这个意义上说，在全球范围内砍伐森林的情况下，关于气候变化的辩论将几乎过时。从这个近乎显而易见的观察出发，我们从统计学的角度来研究人类的生存问题。我们根据确定性的逻辑式动力学对森林和人类之间的相互作用进行建模，同时我们假设人类文明的技术发展是一个随机模型。前者模型已经应用于类似的上下文3、4，而后者基于作为社会技术发展的代理的全球能源消费数据和模型5、6。这使我们的讨论更加可靠，我们表明，保持目前的森林砍伐速度，从统计上讲，在不面临灾难性崩塌的情况下存活下来的可能性非常低。我们将这样的生存概率与人类传播和开发整个太阳系资源的能力联系起来。根据卡戴舍夫等级7，8，该等级根据文明能够使用的能量来衡量文明的技术进步水平，为了在太阳系中传播，我们需要能够以≈4 × 10 26瓦特的速率利用太阳辐射的能量。(卡戴舍夫等级7，8，根据文明能够使用的能量来衡量文明的技术进步水平)，为了在太阳系中传播，我们需要能够利用太阳辐射的能量，其速率为4瓦特×10 26瓦。我们目前的能源消耗率估计为≈10 13瓦9。正如下一节的“技术发展的统计模型”和“数字结果”小节所示，成功的结果有一个明确的阈值，我们得出的结论是，避免灾难性崩溃的可能性非常低，在最乐观的估计中低于10%。

2.2000年至2012年间，全球230万平方公里的森林被砍伐10，相当于每年砍伐2 × 105km2。按照这个速度，所有的森林将在大约100-200年内消失。显然，认为只有当最后一棵树被砍伐时，人类社会才会开始受到森林砍伐的影响，这是不切实际的。森林砍伐造成的环境逐渐退化将严重影响人类社会，因此人类的崩溃将开始得更早。

奇怪的是，我们星球的现状与3中描述的复活节岛森林砍伐有很多相似之处。因此，我们使用该参考文献中介绍的模型来大致描述人与森林的相互作用。诚然，我们在这里的目标不是一个精确的、详尽的模型。建立这样的模型可能是不可能的。我们在以下部分提出和说明的是一个简化的模型，但它允许我们推断所涉及的过程的时间尺度：即描述人口和资源(森林)消费的确定性过程和定义社会的经济和技术增长的随机过程。在3(S)中采用该模型

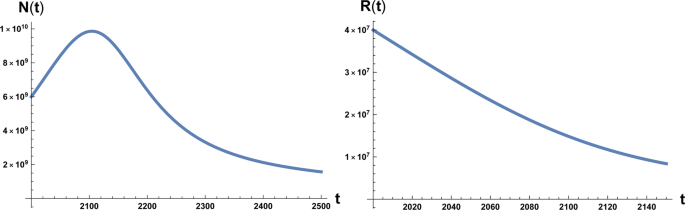
系统(1)和(2)的时间演化如图1和图2所示。我们注意到，在图1中，函数N(T)的最大值的数值是估计为地球人口14的承载能力的N M ~ 10 10。我们必须再次强调，认为在强烈环境退化的情况下人口的下降是非混沌和有序的下降是不切实际的，这也是我们把人口中的最大值和发生的时间作为地球人口14的点的方式。我们必须强调，认为在强烈环境退化的情况下人口的下降是不现实的，这也是我们把人口中的最大值和发生的时间作为地球人口14的点的方式。这也是我们认为在强烈环境退化的情况下人口的下降是不现实的。即“不退货”点。

左边是方程的解的曲线图。(1)初始条件N0 = 6 × 109在初始时间t = 2000A.C.右边：方程的解的曲线图。(2)初始条件为R0 = 4 × 10 7，这里为β = 70 0和a 0 = 10−12。

左边是方程的解的曲线图。(1)初始条件N0 = 6 × 109在初始时间t = 2000A.C.右边：方程的解的曲线图。(2)初始条件为R0 = 4 × 10 7，这里为β = 170和a 0 = 10−12。

根据卡戴舍夫等级7，8，为了能够在太阳系中传播，文明必须能够建造戴森球体16，即最大限度地技术利用其本地恒星的大部分能量，对于有太阳的地球来说，这相当于E D ≈ 4 × 10 26瓦的能量消耗，我们称之为戴森极限。我们的实际能源消耗估计在E c ≈ 10 13瓦(世界能源统计评论)9.为了描述我们的技术发展，我们可以粗略地将发展图解为一个二分法的随机过程。

其中，T是人类文明的技术发展水平，我们也可以将其与能源消耗联系在一起。α是描述技术增长率(即T)的常数，ξ(T)是值为0，1的随机变量。因此，我们认为，基于全球能源消费数据5，6是指数增长，波动主要反映全球经济的变化。因此，我们考虑一个调制指数增长过程，其中增长率的波动被变量ξ(T)捕获。该变量以密度ψ(T)分布的开关之间的等待时间在值0、1之间切换。当ξ(T) = 0时，增长停止，当ξ切换到ξ(T) = 1时，增长恢复。如果我们更严格地考虑T来描述技术发展，ξ(T)反映了这样一个事实，即研究投资可能会因为经济增长和危机时期的交替而中断。通过以下转换，

关于t的两边的区分，并使用公式。(5)，对于变换后的变量W，我们得到。

其中\(\bar{\xi}(T)=2[\xi(T)-\langle\xi\range]\)和<ξ>是ξ(T)的平均值，因此\(\bar{\xi}(T)\)取值±1。

上述方程已被深入研究，由一般等待时间分布产生的概率分布P(W，t)的一般解可以在文献17中找到。知道了该分布，我们可以在达到必要的技术水平时评估第一通过时间分布，例如生活在地外空间或发展任何其他方式来维持地球上的人口。必须将这一特征时间与到达不返回点所需的时间进行比较。知道第一次通过的时间分布18，我们将能够评估我们的文明生存的可能性。

如果二分过程是具有速率γ的泊松过程，则相关函数是指数的，即。

和方程。(7)为概率密度生成著名的电报员方程。

我们注意到，我们所遵循的方法是基于这样的假设：在随机时间，指数分布的速率γ，二分变量\(\bar{\xi}\)改变它的值。在此假设下，给出了方程的解。(9)是。

其中，i_n(Z)是第一类修正的贝塞尔函数。转换回我们拥有的变量T。

$$\BEGIN{array}{ccc}{f}_{T}(T)&；=&；\EXP\Left[-\Frc{\Gamma}{2}t\Right]\Frc{\Gamma\sqrt{x-{x}_{1}}{I}_{1}\left(\frac{\sqrt{x-{x}_{1}}\sqrt{t-\frac{x-{x}_{1}}{2}}\gamma}{\sqrt{2}}\right)}{2\sqrt{2}\sqrt{t-\frac{x-{x}。_{1}}{2}\theta\Left[t-\frac{x-{x}_{1}}{2}\right]\\&；&；+\，\exp\Left[-\frac{\Gamma}{2}t\Right]\Delta\Left(t-\frac{x-{x}_{1}}{2}\Right)，\end{array}$$。

这一点通过数值模拟得到了证实(见图3)。首次获得点x的平均时间由下式给出。

有趣的是，这是发生纯指数增长所需时间的两倍，这取决于T的终值和初值之间的比率，并且与γ无关。我们还强调，这一结果取决于与所考虑的文明的发展阶段直接相关的参数，即我们假设为文明进化的完全工业化阶段的能源消耗Ec的起始值T1和假定为戴森极限ED的终止值T，以及技术增长率α。对于后者，我们可以相当乐观地选择值α = 0.345，遵循摩尔定律20(见下一节)。使用上面的数据，相对于我们星球的情景，我们得到了<t> ≈ 180年的估计。从图1和图2我们可以看到，对β = 700和β = 170的不返回时间的估计分别为130年和22年，后者是最现实的值。在任何一种情况下，这些基于平均值的估计都不到180年，对于避免灾难性的崩溃来说，已经预示着不会有一个有利的结果。尽管如此，为了估计避免崩塌的实际概率，我们不能依赖平均值，但我们需要评估单个轨迹，并计算在“不返回点”之前成功达到戴森极限的轨迹。我们在数值上实现这一点，如下所述。

(左)比较方程的理论预测。(15)(黑色曲线)和方程的数值模拟。(3)(青色曲线)用于γ = 4(任意单位)。(右)比较公式的理论预测。(15)(红色曲线)和方程的数值模拟。(3)(黑色曲线)表示γ = 1/4(任意单位)。

(左图)在到达“无回程”点之前达到戴森值的概率p_(Suc)是α的函数，对于β = 170是a的函数。参数a用Km2ys−1表示。(右面板) = 1.5 × 10−4 km 2 ys−1作为α的函数的p suc的二维曲线图。红线是β = 170次航班的红线。黑色连续线(无法区分)分别适用于β = 300型和700型(另见图6)。绿色虚线表示符合摩尔定律的α值。

我们对情商进行模拟。(1)、(2)和(5)对于固定的α和参数a_0的不同取值，我们统计了在总体水平达到“不可返回点”之前达到β极限的轨迹数，在此之后发生了快速崩塌。更确切地说，由于二叉随机过程ξ(T)，T的演化是随机的，所以我们生成T(T)轨迹，同时跟踪由EQS的动态决定的种群和森林密度的演化。(1)，(2)3，直到后一种动力学达到不返回点(种群最大，然后崩溃)。当这种情况发生时，如果T(T)中的轨迹已经达到戴森极限，我们将其视为成功，否则视为失败。这样我们就确定了图5、图6和图7中的概率和相对平均时间。采用弱可持续性的观点，我们的模型没有具体说明成功的轨迹能够找到替代森林并避免坍塌的技术机制，我们没有定义这一点，而是专门地和概率地将其与戴森极限的达到联系起来。值得注意的是，我们将公式所描述的技术增长过程联系起来。(5)经济增长对经济增长的影响，因此，对于经济和技术增长，我们认为是一个随机的增长和停滞周期序列，根据对推动世界经济的估计，即根据国家经济研究局的估计，平均周期约为1年和4年。

平均时间τ(以年为单位)在达到“不返回”点(成功，左)之前达到戴森值，并且没有达到戴森值(失败，右)，这是α的函数，a表示β = 170。平台区(左面板)，其中τ ≥ 50对应于发散的τ，即在命中“止回”点之前未达到戴森值，因此出现故障。τ = 0(右侧面板)的平台区对应于未发生故障，即成功。参数a用Km2ys−1表示。

根据α和β = 300(左)和700(右)的函数，在命中“不返回”点之前达到戴森值的概率psuc。参数a用Km2ys−1表示。

作为β和α的函数，对于 = 1.5 × 10−4 km 2 ys−1，在到达“不返回”点之前达到戴森值p suc的概率。

在等式中。(1，2)我们将变量重新定义为N‘ = N/R W和R’ = R/R W，其中\({R}_{W}\simeq150\x{10}^{6}\，K{m}^{2}\)大陆总面积，相应地用 = a 0 × R W = 1.5 × 10−4 km 2 ys−1替换参数a0。我们分别根据当前森林面积和人口，从数值\({R{\素数}}_{0}\)和\({N{\素数}}_{0}\)开始进行相应的模拟。我们取a从10−5到3 × 10−4 km 2 ys−1和α从0.01ys−1到4.4ys−1的值。结果如图4和图6所示。图4显示了参数α的阈值，即技术增长率，超过该阈值有非零的成功概率。该阈值随着另一个参数a的值而增加。如图7所示，该值还取决于β的值，并且较高的β值对应于更有利的场景，在该场景中，对于较小的α，即对于较小的、更容易获得的值，向成功的非零概率的转变发生。更具体地说，图4的左面板显示，对于更现实的值β = 170，具有避免崩溃的非零概率的参数值区域对应于大于0.5时的α的值。因此，即使假设技术增长率与摩尔定律给出的价值对数(α = (2)/2 = 0.345 ys−1)相当(相当于每两年规模翻一番)，也不太可能避免达到灾难性的“不返回点”。当 = 1.5km2× 104km2的实际值按公式估算的 1时，−1。(4)，实际上，即使采用对应于β = 700时的更乐观的情况(图4中右面板中的黑色曲线)，也可以获得小于10%的概率来避免以摩尔增长率崩溃。而需要大于1.5时的α才能在以下情况下具有避免崩溃的非零概率。

.