去功能化与弗莱德定理

函数式编程的主要思想是像对待任何其他数据类型一样对待函数。特别是，我们希望能够将函数作为参数传递给其他函数，将它们作为值返回，并将它们存储在数据结构中。但是函数是哪种数据类型呢？它是一种类型，当与另一段称为参数的数据配对时，可以将其传递给名为Apply的函数以产生结果。

在实践中，函数应用隐含在语言的语法中。但是，正如我们将看到的，即使您的语言不支持高阶函数，您所需要的就是推出您自己的Apply。

但是，这些函数对象(要应用的参数)从何而来？内置应用程序如何知道如何处理它们？

在实现函数时，从某种意义上说，您是在告诉Apply如何处理它-要执行哪些代码。您正在实现Apply的各个块。这些块通常散布在您的程序中，有时以lambdas的形式匿名。

我们将讨论在不更改程序语义的情况下引入更多函数、用命名函数替换匿名函数或将某些函数转换为数据类型的程序转换。这种转换的主要优势在于，它们可以提高性能，有时会极大地提高性能；或者支持分布式计算。

一如既往，我们期待范畴论为定义函数对象提供理论基础。事实证明，我们能够进行函数式编程，因为类型和函数的范畴是笛卡尔闭合的。第一部分，笛卡尔，意味着我们可以定义产品类型。在Haskell中，我们在语言中内置了对类型(a，b)。明确地说，我们会把它写成。Product在这两个参数中都是函数式的，因此，我们可以特别定义一个函数式。

定义函数类型(也称为指数对象)。这个附加词的存在使范畴成为封闭的。您可以将这两个函数器分别识别为写入器和读取器函数器。当该参数被限制为Monid时，写入器函数器变成Monad(读取器已经是Monad)。

咖喱：：(C，a)->；d)->；(c->；(a->；d))取消咖喱：：(c->；(a->；d)->；((c，a)->；d)

在我上一篇博客文章中，我从范畴的角度讨论了Freyd的伴随函子定理。在这里，我将尝试对其进行编程解释。另外，原始定理是通过寻找给定函子的左伴随来表述的。在这里，我们感兴趣的是寻找乘积函子的正确伴随。这不是问题，因为范畴论中的每个结构都可以通过颠倒箭头来对偶。因此，我们不考虑逗号类别，而是使用逗号类别。它的对象是对，其中是一个态射。

这是大体情况，但在我们的例子中，我们处理的是单个类别，并且是一个内函数。我们可以在Haskell中实现逗号类别的对象。

我们正试图构造一个表示函数a->；d的函数对象，那么c在这一切中扮演什么角色呢？要理解这一点，您必须考虑到函数对象可用于描述闭包：从其环境中捕获值的函数。类型C表示这些捕获的值。稍后，当我们讨论使闭包失效时，我们将更明确地看到这一点。

我们的逗号类别是从到的所有闭包的类别，同时捕获所有可能的环境。我们正在构造的函数对象本质上是所有这些闭包的总和，只是其中一些闭包被多次计数，所以我们需要执行一些标识。这就是态射的作用。

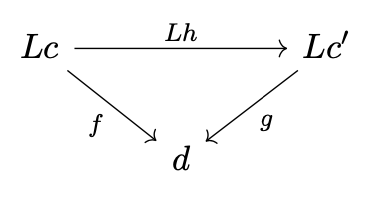
逗号范畴的态射是构成交换三角形的态射。

不幸的是，通勤图表不能用Haskell表示。我们能得到的最接近的结论是，一个来自。

C1=逗号c f：：(C，a)->；d c2=逗号c&39；g g：：(C'；，a)->；d。

这里，bimap hid是将h提升到函数器。更明确地说

当我们将c解释为定义闭包的环境时，问题是：f使用的是用c编码的所有信息，还是只使用其中的一部分？如果这只是一部分，我们就可以把它分解出来。例如，考虑一个捕获整数的lambda，但它只对整数是偶数还是奇数感兴趣。我们可以用捕获布尔值的lambda替换这个lambda，甚至可以使用该函数来转换环境。

构造中的下一步是将投影函数器从逗号类别定义回忘记部分而只保留对象的函数。

我们使用此函数器在中定义图。现在，我们不再像在上一期文章中那样取其极限，而是取此图的列限制。我们将使用这个Colimit来定义右伴随函数器在上的动作。

在我们的例子中，健忘的函数器丢弃逗号dc的函数部分，只保留环境。这意味着，只要d不是void，我们处理的就是一个包含我们类型类别中的所有对象的巨型图。这个图的界限是一切的巨大余积，由逗号范畴的态射引入的模标识。但是，这些标识对于删除多余的闭包至关重要。可以用使用简化环境的更简单的lambda来标识仅使用来自捕获环境的部分信息的每个lambda。

为了进行说明，考虑构造函数对象或(到终端对象的幂)的一个有点极端的情况。此对象应与同构。让我们看看这是如何工作的：终端对象是产品的单位，所以。

所以逗号类别就是箭头的切片类别。碰巧这个类别有终端对象。具有终端对象图表的列限制是终端对象。因此，实际上，在本例中，我们的构造产生了一个与同构的函数对象。

直观地说，给定一个从环境中捕获类型值并返回a的lambda，我们可以简单地将其分解出来，使用该lambda将环境转换为，然后将标识应用于。后者对应于逗号类别对象，健忘函数器将其映射到。

多运行几个示例来掌握它的诀窍是很有指导意义的。例如，函数对象Bool->；d可以通过考虑以下类型的闭包来构造

H：：c->；(d，d)hc=(f(c，True)，f(c，False))。

G：：((d，d)，Bool)->；d g((d1，d2)，b)=如果b，则d1否则d2。

我们对这个附加项目特别感兴趣。它的成分at是一个态射。

实际上，它就是该类别中的终端对象。您可以看到这一点，因为对于任何其他对象，都有一个使下面的三角形互换的态射：

这个态射是末端COO锥中的一条腿，它定义。我们可以肯定地知道它在椰子锥的底部，因为它是。

要深入了解函数对象的结构，假设您可以枚举所有可能的环境集。然后，逗号类别将由对组成。所有这些环境的副产品都是功能对象的一个很好的候选者。事实上，让我们试着为它定义一个Counit：

和的映射是映射的乘积这一事实。右手边可以由逗号范畴的态射构成。

因此，该对象至少满足函数对象的一个要求：有一个申请它的实现。不过，这是高度冗余的。这就是为什么我们在构造函数对象时使用colimit而不是联积的原因。另外，我们忽略了尺寸问题。

正如我们之前讨论过的，由于大小问题，此结构一般不起作用：逗号类别不一定很小，并且可能不存在逗号限制。

为了解决这个问题，我们以前定义了较小的解决方案集。在右伴随的情况下，解集是弱末端的对象族。这些配对，在它们之间，可以分解出任何。

这意味着我们总能找到一个指数和一个态射来满足这个方程。每一个都可能需要一个不同的AND来考虑，但对于任何一个，我们都保证总是能找到一对。

一旦我们有了一个完整的解集，右伴随就是通过首先形成所有的余积，然后使用余均衡器来构造一个终端对象来构造的。

真正有趣的是，在某些情况下，我们可以只使用解集的余积来近似伴随项(从而跳过均衡器部分)。

我们的想法是，在特定的程序中，我们不需要表示所有可能的函数类型，只需要表示这些类型的(小)子集。我们也不特别担心唯一性：如果相同的函数以多个语法表示结束，这是没有问题的。

让我们用编程术语重新表述Freyd对函数对象的构造。解集是类型和函数的集合，使得对于我们的程序中感兴趣的任何函数(例如，用作另一个函数的参数)存在一个和函数，从而可以重写，换言之，每个感兴趣的函数都可以被解集函数中的一个替换。该标准功能的环境总是可以从更一般功能的环境中提取。

高阶函数的一个特殊应用出现在连续传递变换的上下文中。让我们看一个简单的例子。我们将实现一个函数，该函数遍历包含字符串的二叉树，并将它们全部连接成一个字符串。这就是那棵树

Show1：：tree->；string show1(叶s)=s show1(节点l s r)=show1 l++s++show1 r。

树：：树=节点(Node(Leaf"；1"；)"；2"；(Leaf"；3"；))"；4"；(Leaf"；5"；)。

只有一个问题：递归消耗运行时堆栈，而运行时堆栈通常是有限的资源。您的程序可能会用完堆栈空间，从而导致“堆栈溢出”运行时错误。这就是编译器只要有可能就会将递归转换为迭代的原因。如果函数是尾递归的，也就是说，递归调用是函数中的最后一个调用，则始终是可能的。尾递归函数中不允许对递归调用结果执行任何操作。

在我们的show1实现中，这显然没有发生：在进行递归调用以遍历左子树之后，我们仍然需要进行另一次调用来遍历右子树，并且两个结果必须与节点的内容连接在一起。

请注意，这不仅仅是一个函数式编程问题。在以迭代为规则的命令式语言中，树遍历仍然是使用递归实现的。这是因为数据结构本身是递归的。实现非递归树遍历曾经是一个常见的面试问题，但解决方案总是显式地实现您自己的堆栈(我们将在本文的末尾看到它是如何实现的)。

有一个使用连续传递样式(CPS)使函数尾递归的标准过程。想法很简单：如果函数调用的结果有问题，就让我们调用的函数来做。这个“要做的事”叫做延续。我们正在调用的函数将Continue作为参数，当它完成其工作时，它将使用结果调用它。延续是一个函数，因此CPS转换的函数必须是高阶的：它们必须接受函数作为参数。通常，延续是使用lambdas现场定义的。

下面是CPS转换后的树遍历。它不是返回字符串，而是接受延续k，这是一个接受字符串并产生类型a的最终结果的函数。

Show2：：tree->；(String->；a)->；a show2(叶s)k=k s show2(Node Lft S Rgt)k=show2 lft(\ls->；show2 Rgt(\r->；k(ls++s++rs)

如果树只是一片树叶，show2用存储在树叶中的字符串调用Continue。

如果树是一个节点，则show2递归地调用自身以转换左子lft。这是一个尾部调用，不会对其结果做更多操作。取而代之的是，其余的工作被打包到lambda中，并作为show2的延续传递。这就是Lambda。

将使用遍历左子对象的结果调用此lambda。然后，它将使用正确的子级和另一个lambda调用show2。

再说一次，这是一次尾部召唤。这个lambda需要的字符串是遍历正确的子级的结果。它连接左边的字符串、来自当前节点的字符串和右边的字符串，并用它调用原始的延续k。

最后，为了转换整个树t，我们使用一个简单的延续调用show2，该延续接受并立即返回最终结果。

作为延续，lambdas没有什么特别之处。可以用命名函数替换它们。不同之处在于，lambda可以隐式地从其环境中捕获值。命名函数必须显式捕获它们。我们在CPS转换的遍历中使用的三个lambda可以替换为三个命名函数，每个函数都带有一个额外的参数，表示从环境捕获的值：

完成s=s下一个(s，rgt，k)ls=show3 rgt(conc(ls，s，k))conc(ls，s，k)rs=k(ls++s++rs)。

完成的第一个函数是标识函数，它强制将泛型类型a缩小为字符串。

Show3：：tree->；(String->；a)->；a show3(叶s)k=k s show3(Node Lft S Rgt)k=show3 lft(NEXT(s，Rgt，k))show t=show3 t Done。

我们现在可以开始把它与前面讨论的伴随定理联系起来。我们刚才定义的三个函数Done、Next和Conc组成了这个系列。

它们是两个参数或一对参数的函数。第一个参数表示对象，它是解决方案集的一部分。它与闭包捕获的环境相对应。这三个分别是。

所有三个函数的第二个参数都是String类型，返回类型也是String，因此，根据Freyd定理，我们正在定义函数对象，其中是String，也是String。

这里是有趣的部分：我们可以用解决方案集的元素的余积近似它，而不是定义通用函数类型String->；string。这里，SUM类型的三个组件对应于我们的三个函数捕获的环境。

加法运算的COUNIT由此SUM类型的函数近似，该函数与一个字符串配对，返回一个字符串。

Apply：：kont->；string->；string Apply Done s=s Apply(Next S Rgt K)ls=show4 Rgt(Conc Ls S K)Apply(Conc Ls S K)rs=Apply k(ls++s++rs)。

我们可以传递此SUM类型，而不是将三个函数中的一个传递给我们的高阶CPS遍历

Show4：：tree->；kont->；string show4(叶s)k=应用k s show4(Node Lft S Rgt)k=show4 lft(下一个s Rgt k)。

通过用Apply函数配备的数据类型替换它们的函数参数，我们删除了所有高阶函数。在几种情况下，这是有利的。在过程化语言中，去函数化可以用来用循环代替递归。事实上，可以将Kont数据结构视为用户定义的堆栈，特别是在将其重写为列表的情况下。

在这里，Done被替换为一个空列表，Next和conc一起对应于将一个值推入堆栈。

在Haskell中，编译器执行尾递归优化，但去功能化在实现分布式系统或Web服务器时可能仍然有用。任何时候我们需要在客户端和服务器之间传递函数时，我们都可以将其替换为易于序列化的数据类型。

(在C++中)您可以将函数视为临时类实例-只有一个方法的类。因此，调用函数与执行类实例化和调用方法非常相似。