泰勒级数与加速度计

在我的“程序员数学入门”一书中，我将泰勒级数描述为“钉钉子的锤子”。我从Hammack、Ryan和Ziech的“八个令人惊叹的工程故事”中了解到现代智能手机加速计设计中的另一个钉子，我将在这里与大家分享。

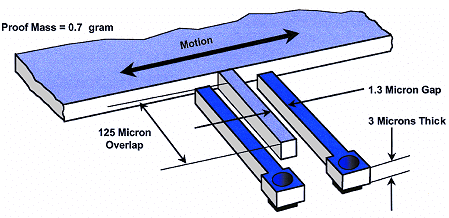
这些加速度计是使用包含三个板的系统设计的，这三个板对应于两个电容器。简单回顾一下我对电容器工作原理的(有限的)理解。包含两个导电板的电容器如下所示：

电池提供的电压将电子推向负方向，或等效地将“电荷”推向正方向(参见电荷流和电子流之间的区别)。这些选举在标有标签的板上积累起来，两个板上的电荷差异产生了一个电场。如果电场足够强，电子就可以跳跃到正极板的间隙，完成电路。否则，极板达到“容量”，电流停止流动。是否发生跳跃或电流停止取决于极板的面积、极板之间的距离以及极板之间材料的性质，最后一个称为“介电常数”。(注意，我不确定为什么它不取决于极板的组成材料，但我想如果有必要的话，它可以平滑到介电常数中)这个关系可以用公式来概括。(注意，我不确定为什么它不取决于极板的材料，但我想如果有必要的话，它可以平滑到介电常数。

然后，外部事件可能会导致两个平板移动到足够近的距离，这样电子就可以跳过间隙，电流就可以开始流动。这会使带负电的极板放电。

只需固定带负电的板的一端，就可以让带负电的板稍微晃动一下，就像跳水板(悬臂)一样。

根据弹簧的胡克定律，摆动量将与加速度成正比。

当移位一段距离时，极板中的电容变为。

它能够测量一维上的加速度，所以这些装置中的三个都布置在垂直轴上，这样就可以测量三维空间中的加速度。

这种设计的问题是电容相对于位移量的非线性变化。要查看非线性程度，请将其展开为泰勒级数：

我使用大O符号来更严格地表示我“忽略”所有立方和更高的术语。我之所以能这样做，是因为在这些工程系统中(我在这里相信哈马克的话)，数量是有意义的大，但后来的术语，比如可以忽略不计。当然，只有当位移与之相比非常小时，这才是正确的，这就是为什么大O有一个下标。

显然，通过电容变化中的非线性向后工作是足够困难的，足以保证改变系统的设计。(我不知道为什么这很困难，但我想这与测量设备的工程限制有关；如果您知道更多信息，请务必插话)。

避免这种情况的系统设计是三板系统而不是两板系统。

在该系统中，中间板在连接到电压源的两个固定板之间来回移动。当它远离一个而靠近另一个时，一侧增加的电容被另一侧减少的电容所平衡。泰勒级数显示了这两个变化如何仅在平方项上抵消。

如果表示左板(中板向其移动)的变化的电容，并表示右板(中板向其移动得更远)，则我们通过泰勒级数(对两者使用泰勒级数，但在本例中是)来扩展电容的差异。

同样，由于立方和更高的项可以忽略不计，我们可以“忽略”这些部分。剩下的是对中板位移变化的线性响应。这使得它更容易测量。因为我们测量的是电容的差异，所以这种设计被称为“差动电容器”。

虽然回过头来看数学是很整洁的，但我很惊讶一个人是如何从头开始构思出这个设计的。发明人有没有注意到泰勒级数近似中的对称性可以被安排成相互否定的？有没有其他类型的“身体直觉”在起作用？