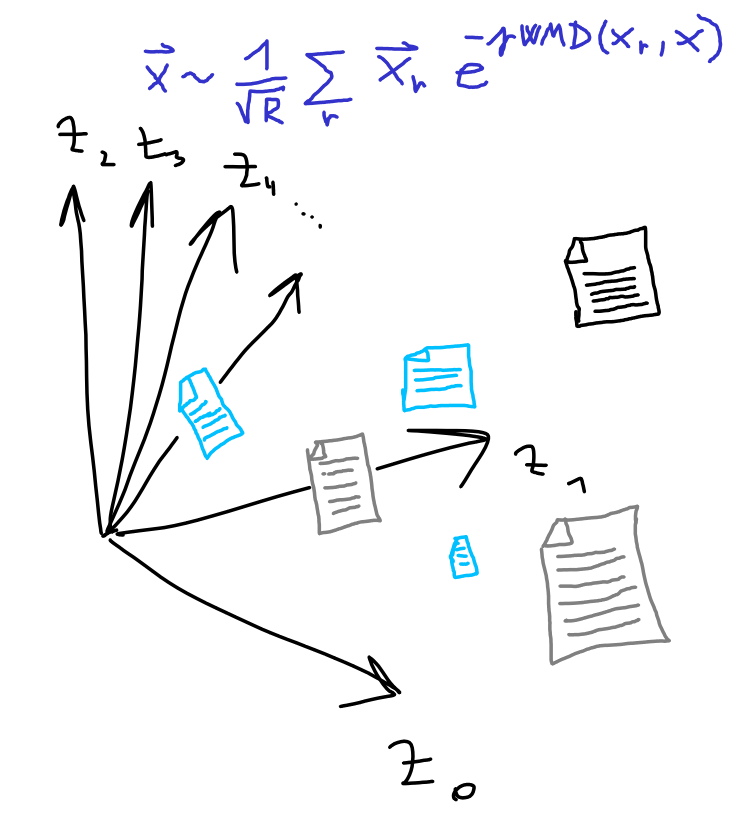
Word Mover的嵌入：廉价的文档WMD

它是将一堆泥土转化为另一堆泥土所需的最小污泥量乘以距离。

尽管名字中有地球，但更好的类比是交通问题。运输问题的一个很好的例子是黄金矿石从矿山到精炼厂的运输成本优化，在这种情况下，每个精炼厂只能接受一定比例的矿石。

土工距离也是概率分布之间的距离度量，因此上述问题可以重新表述为以下问题。如何将金矿的这种地理分布转化为运输成本最低的这种地理分布？

土石方距离的计算复杂度是超立方的，可以在网络流：理论，算法和应用中找到。有关于在一般情况下用二次复杂度近似EMD和在允许预计算的情况下在文档搜索中用线性复杂度近似EMD的论文。

词嵌入加权平均嵌入是计算文档中词向量的频率加权平均的向量，用于wewa的相似度度量为余弦相似度。

与WEWA的O(L)相比，WMD的复杂度为O(L^3\log(L))，其中L\为文档长度。

将嵌入计算复杂度的BERT转换器模型语句与WMD进行比较会很有趣。如果我理解正确，BERT在文档长度上是线性复杂度的，尽管BERT的总运行时间在许多情况下可能仍然更长。Google有一个叫做Bleurt的句子相似度模型。

就分类精度而言，伯特肯定会赢，但我想知道差距有多大。

在过于简化的术语中，Word Mover的嵌入是文档的向量嵌入，使得它与集合中的文档的点积接近Word Mover在文档之间的距离，从而减少计算成本。

为了解决主要的计算复杂性，我们需要降低WMD计算的成本。我们能不能使WMD计算的每一边中的一个文档更小？对于小的恒定大小\(D\)文档\(ω\)，WMD的复杂度将接近线性\(O(L\log(L))\)而不是\(O(L^3\log(L))\)！因此，如果我们可以将所有文档不是相互比较，而是与\(R\)个小得多的文档进行比较，那么WMD的复杂度将几乎是线性的\(O(L\log(L))\)！因此，如果我们可以将所有文档不相互比较，而是与\(R\)个小得多的文档进行比较，我们可以将复杂度从\(O(N^2L^3\log(L))\)降到\(O(NRL\log(L))\)！

嵌入的第j维值是使用到由\(\ω_j\)表示的“随机生成的文档”的WMD距离来定义的。

让我们暂时假设我们知道如何随机生成文档。为什么上面说得通呢？

如上所述，嵌入的点积由位于文档之间最短路径上的随机文档主导，请注意，如果随机文档足够“丰富”，则它只能接近文档之间的最短路径。

\(\mathit{wme}(X)\cdot\mathit{wme}(Y)=\)\(\frac{1}{R}\sum_j\exp[-\Gamma(\mathit{wmd}(x，\omega_j)+\mathit{wmd}(y，\omega_j))]\)\(\近似\frac{1}{R}exp[-\Gamma(wmd(x，\omega_k)]\)\(\约\frac{1}{R}\exp[-\Gamma\mathit{wmd}(x，y)]\)。

您对生成随机文档持怀疑态度，这是正确的。我们不需要生成太多的文档吗，这会使我们加速计算的努力落空？我们如何生成文档呢？

为了生成文档，我们只需要生成足够的随机词向量来表示单词，也许为了证明的目的或者为了具有生成“混合单词”的能力，WME论文生成随机向量而不是来自字典的随机单词，然后为它们绘制单词。

文章引用了一个观察结果，即词2vec和手套词向量的方向分布是近似各向同性的，即归一化词向量在单位球面上均匀分布，我们可以通过从超立方体中均匀采样，然后对结果进行归一化来生成归一化词向量。

但是每个随机文档多少字就够了？如果我们生成太大的文档，我们不会获得任何加速！到目前为止，我还没有提到对我们想要嵌入的文档集合的任何限制。它来了。

本文观察到，文档集合中主题个数量级的随机字数量是足够的，因此，如果我们的文档集合的主题数足够小，应该可以在降低时间复杂度的同时获得较好的准确率。

由于收敛速度快，论文发现数千个数量级的数量就足够了，这也是他们测试数据集中的文档数量的数量级，我不确定集合中的文档数量需要多少个才会更多。

生成\(R\)个随机文档：对于所有输入文档，计算Word Mover对刚生成的文档的嵌入投影，并将其存储到矩阵\(Z\)。

该近似是基于下面定义的词移动核收敛到WMD的解析证明，证明利用随机特征理论来证明WME之间的内积收敛到可以解释为WMD的软版本的正定核。

当随机文档大小(主题计数)不变时，方法复杂度为O(NRL\log(L))。与KNN-WMD变种(O(N^2L^3log(L)相比，WME在分类精度上略优于KNN-WMD。