皮克定理

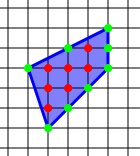
跳转到导航跳转要搜索在等距点(即，具有整数坐标点)网格上构建的简单多边形，使得该多边形的所有顶点都是网格点，则Pick定理提供了一个简单的公式，用于根据位于多边形内部的格点数量i和放置在多边形周长上的边界上的格点数量b来计算该多边形的面积A：[1]。

在图中所示的示例中，我们有i=7个内点和b=8个边界点，因此面积为A=A=7+A+8/2，−=1=A=7+B，−=1=0，10个平方单位。

如上所述的定理仅适用于简单多边形，即由单个非自交边界组成的多边形(因此不包含孔)。对于一般多边形，Pick的公式推广到[2][3]。

A=v−1 2 e b+h−1{\DisplayStyle A=v-{\FRAC{1}{2}}e_{b}+h-1}。

其中，v{\displaystyle v}是多边形边界内和多边形边界上的顶点数，e b{\displaystyle e_{b}}是多边形边界上的晶格边数，h{\displaystyle h}是多边形中的孔数。

例如，考虑通过连接点(0，0)，(2，0){\displaystyle(0，0)，(2，0)}生成的"；多边形"；。它有3个顶点、0个孔和0个面积。要使公式起作用，它必须有4条边。因此，人们只需计算每条边两次，每边一次。

1899年，乔治·亚历山大·皮克(Georg Alexander Pick)首次描述了这一结果。[4]Reeve四面体表明，三维空间中不存在类似于Pick定理的，它通过计算多面体的内点和边界点来表示多面体的体积。然而，通过Ehrhart多项式在高维上有一个推广。

考虑一个多边形P和一个三角形T，其中一条边与P相同。假设Pick定理分别对P和T成立；我们想要证明，通过将T加到P得到的多边形PT也是如此。由于P和T共享一条边，所以沿着边的所有公共边界点都合并到内点，除了边的两个端点合并到边界点之外。因此，将公共边界点的数量称为c，我们有[5]

IPT=IPT+ITT+(c−2){\显示样式i_{pt}=i_{P}+i_{T}+(c-2)}。

B P T=b P+b T−2(c−2)−2.{\DisplayStyle b_{pt}=b_{P}+b_{T}-2(c-2)-2。}。

I P+IT=i P T−(c−2){\DisplayStyle i_{P}+I_{T}=i_{pt}-(c-2)}。

B P+b T=b P T+2(c−2)+2.{\显示样式b_{P}+b_{T}=b_{pt}+2(c-2)+2。}。

A P T=A P+A T=(i P+b P 2−1)+(i T+b T 2−1)=i P+I T+b P+b T 2−2。=i P T−(c−2)+b P T+2(c−2)+2 2−2=i P T+b P T 2−1.{\DisplayStyle{\Begin{Alignment}A_{pt}&；=A_{P}+A_{T}\\&；=\Left(i_{P}+{\frac{b_{P}}{2}\右)+\Left(I_{T}+{\frac{b_{T}}{2}}-1\right)\\&；=i_{P}+i_{T}+{\frac{b_{P}+b_{T}}{2}}-2\\&；=i_{pt}-(c-2)+{\frac{b_{pt}+2(c-2)+2}{2}}-2\\&；=i_{pt}+{\frac{b_{pt}}{2}}-1.\end{对准}。

因此，如果该定理适用于由n个三角形构造的多边形，则该定理也适用于由n+1个三角形构造的多边形。对于一般的多面体，众所周知，它们总是可以三角剖分的。这在2维空间是正确的，这是一个简单的事实。要用数学归纳法来完成证明，还需要证明该定理对三角形是成立的。此案例的验证可以通过以下几个简单步骤完成：

由此推论，该公式对任何边与轴平行的矩形都是正确的；

现在，通过附加这样的直角三角形，任何三角形都可以变成矩形；由于公式对直角三角形和矩形都是正确的，所以它也适用于原始三角形。

最后一步使用的事实是，如果定理对于多边形PT和三角形T是真的，那么它对于P也是真的；这可以通过非常类似于上面所示的计算来看到。

设C{\displaystyle C}是R2{\displaystyle\mathbb{R}^{2}}中的有界凸区域，不一定是闭的。然后。

|L(C)|≤Area⁡(C)+12 Perieter⁡(C)+1{\DisplayStyle|L(C)|\leq\OperatorName{Area}(C)+{\frac{1}{2}}\OperatorName{Perieter}(C)+1}。[2]。

其中L(C){\displaystyle L(C)}是C{\displaystyle C}中的格点集合，并且|L(C)|{\displaystyle|L(C)|}是它们的数目。

证明是通过取L(C){\displaystyle L(C)}的凸包C‘{\displaystyle{\bar{C}}，它应该被认为是C{\displaystyle C}的格近似，然后对其应用Pick定理。

|L(C)|=|L(C‘)|=面积⁡(C’)+1 2 B(C‘)+1≤面积⁡(C’)+1 2周长⁡(C‘)+1。显示区域样式(C)+1 2周长样式(C)+1{\≤⁡{\Begin{⁡}|L(C)|=|L({\BAR{C}})|&；=\操作员名称{面积}({\bar{C}})+{\frac{1}{2}}B({\bar{C}})+1\\&；\leq\操作员名称{面积}({\bar{C}})+{\frac{1}{2}}\操作员名称{周长}({\bar{C}})+1\\&；\leq\操作员名称{面积}(C)+{\frac{。

其中B(C‘){\DisplayStyle B({\bar{C}})}是C’{\displaystyle{\bar{C}的边界点的个数，等于它的边数，由于每条边的长度至少为1，B(C‘)≤Perieter⁡(C’){\DisplayStyle B({\BAR{C}})\leq\OperatorName{Perieter}({\BAR{C}})}。阶跃周长⁡(C‘)≤Perieter⁡(C){\DisplayStyle\OperatorName{Perieter}({\BAR{C}})\leq\OperatorName{Perieter}(C)}使用两条嵌套的、凸的、闭合的曲线之间，内曲线较短的性质，这是克罗夫顿公式的一个应用。

当L(C){\displaystyle L(C)}在同一行时，这仍然适用于退化情况。人们只需每条边数两次，每边一次。

^Train，J.。(2007年11月)。Pick定理的初等证明。数学公报。91(522)：536-540。DOI：10.1017/S0025557200182270。

^a b Garbett，Jennifer(2010年11月18日)。格点几何：拾取定理和明可夫斯基定理，数学高级练习(PDF)。存档自原件(PDF)，时间为2017年8月29日。

亚历山大·别利亚耶夫；皮埃尔-阿兰·法约勒(2019-08-08)。计算平行线段：Pick面积定理的新变体。数学智商。41(4)：1-7。DOI：10.1007/s00283-019-09921-8。ISSN电话：0343-6993。

^Pick，Georg(1899)。Geometrisches zur Zahlenlehre"；Geometrisches zur Zahlenlehre"；Sitzungsberichte des Deutschen自然感觉查夫特利希-医学在普拉格的Vereines für Böhmen"；Lotos"；Lots"；Lots"；Sitzungsberichte des Deutschen的自然感觉。(Neue Folge)。19：311-319。JFM33.0216.01.。花旗银行：47270