索迪(氏)六角钢笔

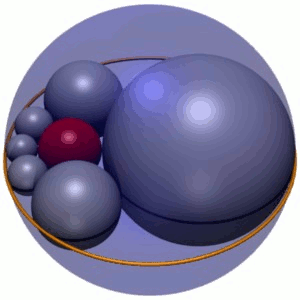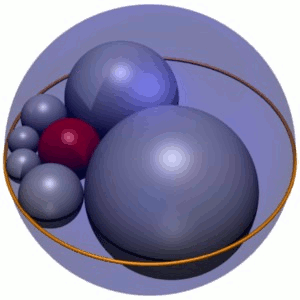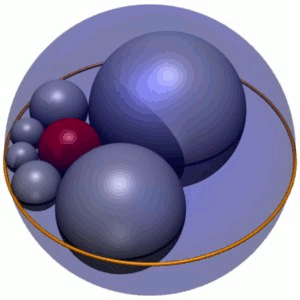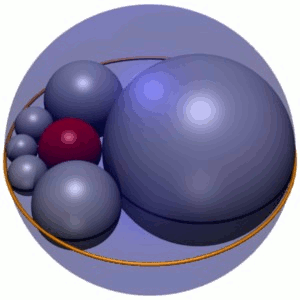
跳转到导航跳转到几何体中搜索，Soddy的六边形是一个由六个球体组成的链(图1中以灰色显示)，每个球体都与其相邻球体相切，也与给定的三个相互相切的球体相切。在图1中，三个球体是蓝色的外层球体，六角形球体中心所在平面上方和下方的两个球体(未显示)。此外，六角球体与第四个球体(图1中的红色)相切，该球体与其他三个球体不相切。

根据弗雷德里克·索迪(Frederick Soddy)在1937年发表的一个定理，[1]对于任何相互相切的球体A、B和C，总是有可能找到一个六边形。实际上，存在一个通过旋转和缩放六角球而相关的无穷族六角球(图1)；在这一点上，苏迪的六角球是六个圆的斯坦纳链的球形类似物。[2]与Steiner链一致，六角球的中心位于椭圆上的单个平面上。正如1822年神奈川县的Sangaku片剂所显示的那样，日本也独立发现了Soddy‘s Sixlet。[3]。

索迪的六边形是一个由六个球体组成的链，标记为S1-S6，每个球体都与三个给定的球体A、B和C相切，这三个球体本身在三个不同的点处相互相切。(为保持本文的一致性，六角球体将始终用灰色表示，球体A和B用绿色表示，球体C用蓝色表示。)。六角球体也与第四个固定球体D(始终显示为红色)相切，该球体与其他三个球体A、B和C不相切。

Soddy的六边形的每个球体也与链中的相邻球体相切；例如，球体S4与S3和S5相切。链是闭合的，这意味着链中的每个球体都有两个相切的邻居；特别是最初和最后的球体S1和S6彼此相切。

环形的索迪六角球是一个特例(图2)，其中三个相互相切的球体由一个半径为r(蓝色)的球体组成，该球体夹在两个垂直距离为2 r的平行平面(绿色)之间。在这种情况下，索迪六角球由六个半径为r的球体组成，这些球体像滚珠轴承一样围绕中心球体排列，并且同样被夹在中间球体中。六角球体也与第四个球体(红色)相切，该球体与其他三个球体不相切。

六个球体的链可以围绕中心球体旋转，而不会影响它们的切线，这表明对于这种情况存在无穷族的解。当它们旋转时，六角形的球体描绘出一个圆环(甜甜圈形状的表面)；换句话说，圆环就是这一族六角形的包络。

求三个给定的相切球体A、B和C的六边形的一般问题可以利用反演简化为环形情况。这种几何运算总是将球体变换成球体或平面，这可以被认为是无限半径的球体。当且仅当球体通过反转中心时，球体才变换为平面。反转的一个优点是它保留了相切；如果两个球体在变换之前是相切的，那么在变换之后它们将保持相切。因此，如果反转变换选择得当，问题就可以简化为更简单的情况，如环形的索迪六边形。反转是可逆的；在同一点重复反转将变换的对象返回到其原始大小和位置。

球体A和B的切点上的反转将它们变换成平行的平面，可以表示为a和b。由于球体C与A和B都相切，并且不通过反转中心，所以C被变换成与这两个平面都相切的另一个球体c；因此，c被夹在两个平面a和b之间。这是环形的Soddy六边形(图2)。六个球体S1-S6可以围绕C包装，并且同样地夹在边界平面A和B之间。重新反转恢复三个原始球体，并将S1-S6变换成用于原始问题的六边形。一般来说，这些六角球S1-S6具有不同的半径。

在重新反转六个球S1-S6之前，可以通过在它们的平面内将六个球S1-S6旋转任意角度来产生无限种类的六角形。这种旋转产生的包络是围绕球体c的环面，它夹在a和b两个平面之间；因此，环面的内径为r，外径为3r。在重新反转之后，这个环面变成了杜平圆周(图3)。

Soddy‘s六边形的封套是一个杜平圆环，是圆环的反转。因此，Soddy的构造表明，杜平的一个圆环以两种不同的方式是一个1参数球体族的包络，并且任一族中的每个球体都与同一族中的两个球体和另一个族中的三个球体相切。[4]查尔斯·杜平(Charles Dupin)可能知道这一结果，他在1803年加斯帕德·蒙格(Gaspard Monge)的论文中发现了以他的名字命名的自行车。[5]。

六边形与其球心平面的交集产生六个圆的斯坦纳链。

在任何椭圆六角形中，例如文章顶部所示的椭圆六角形，都有两个与该六角形相切的平面。为了使椭圆六角形存在，C的半径必须小于A的四分之一。如果C的半径是A的四分之一，那么每个球体在旅途中都会变成一个平面。不过，倒置的图像显示的是正常的椭圆六角形，而在抛物线六角形中，球体变成平面的点正好是它的倒置图像通过倒置中心的时候。在这样的六角形中，只有一个与六角形相切的平面。抛物线六角形的中心线是抛物线。

如果C更大，则形成一个双曲六角形，现在根本没有切面。因此，S1在成为一个平面(它的反像穿过反转中心)，然后反转它的凹面(它的反像围绕着反转中心)之前是走不了多远的。现在，中心线是一条双曲线。

极限情况是当A、B和C的大小都相同时。六角形现在变直了。S1很小，因为它穿过A、B和C之间的孔，并逐渐增长，直到它变成与它们相切的平面。反演的中心现在也与S6的像相切，所以它也是与A、B和C相切的平面。当S1继续进行时，它的凹性被反转，现在它围绕着与A、B、C、S2和S6相切的所有其他球面。S2向上推并增长为切面，S6收缩。然后，S1获得S6的先前位置作为切面。然后，它再次反转凹度，再次穿过这个洞，开始另一次往返旅行。现在，中心线是一条退化的双曲线，在那里它已经坍塌成两条直线。[2]。

日本数学家在索迪之前100多年发现了同样的六角形。他们分析了圆和多边形、球和多面体接触的布局问题，并经常在西方数学家发现相关定理之前独立地找到了这些定理。他们经常把这些作为僧伽库出版。关于六边形的行宫是由Irisawa ShintarōHiroatsu在内田岩美学校制作的，并于1822年5月献给三木川神社。原来的僧伽库已经丢失，但在1832年内田的“Kokonsankan”一书中有记载。2009年8月，根据这份记录制作了一个桑加库的复制品，并将其献给了三木川神社的Hō德库博物馆。[6]。

饭泽三郎的“圣歌”由三个问题组成。第三个问题与索迪的六角形有关：外接球体的直径是30太阳。核球的直径分别为10太阳和6太阳。球链中的一个球的直径是5太阳。然后我问剩余的球的直径。答案是15个太阳，10个太阳，3.75个太阳，2.5个太阳和2个8/11太阳。"；[7]

在他的回答中，写下了计算球直径的方法，可以考虑用现代天平给出以下公式。[需要澄清]如果外球的直径与每个核球的直径之比为1，a2，如果直径与链球的直径之比为c1，……，c6。我们希望用a1，a2和c1来表示c2，…，c6。如果。

K=3(a1a2+a2c1+c1a1−(a1+a2+c1+12)2){\displaystyle K={\sqrt{3\left(a_{1}a_{2}+a_{2}c_{1}+c_。{1}a_{1}-\Left({\Frac{a_{1}+a_{2}+c_{1}+1}{2}}\right)^{2}\right)}}}。

C2=(a1+a2+c1−1)/2−K c3=(3a1+3a2−c1−3)/2−K c4=2a1+2a2。−c 1−2 c 5=(3a 1+3 a 2−c 1−3)/2+K c 6=(a 1+a 2+c 1−1)/2+K。{\DisplayStyle{\begin{aligned}c_{2}&；=(a_{1}+a_{2}+c_{1}-1)/2-K\\c_{3}&；=(3a_{1}+3a_{2}-c_{1}-3)/2-K\\c_{4}&；=2a_{1}+2a_{2}-c_{1}-2\\c_{5}&；=(3a_{1}+3a_{2}-c_{1}-3)/2+K\\c_{6}&；=(a_{1}+a_{2}+c_{1}-1)/2+K.\end{aligned}}}.。

1r1+1r4=1r2+1r5=1r3+1r6。{\displaystyle{\frac{1}{r_{1}+{\frac{1}{r_{4}={\frac{1}{r_{2}+{\frac{1}{r_{5}={\frac{1}{r_{3}+{\frac{1}{r_{6}。

天野，浩史(1992年)，神奈川县的Sangaku收藏(日语中的神奈川-Ken Sangaku-syū)，天野，浩史。

福川秀敏；罗斯曼，托尼(2008年)，“神圣数学：日本神庙几何”，普林斯顿大学出版社，ISBN978-0-691-12745-3。

O'；Connor，John J.；Robertson，Edmund F.(2000)，#34；Pierre Charles François Dupin&34；，MacTutor数学史档案。

索迪，弗雷德里克(1937年)，“整数碗与六角形”，自然，伦敦，第139(350)：77-79页，doi：10.1038/139077a0。

题名/责任者：The On-to-to-deed/Wishida，Tomomi，Edds.。2009年出版，“和散词典”，浅仓，ISBN978-4-254-11122-4。

回路机上的日式寺庙几何(2019年3月19日存档)--SANGAKU问题0的动画0展示了球体A、B的半径相等，球体A、B、C的圆心在线的情况。动画1显示球体A和B的半径彼此相等并且球体A、B和C的中心不在直线上的情况。动画2表示球体A和球体B的半径不相等的情况。动画3显示球体A、B和C的中心在直线上并且球体A和B的半径可变的情况。

在三木川神社的Hō德库博物馆里的桑加库复制品(存档于2016年8月26日)-第三个问题与索迪的六边形有关。