Bean Machine-一种声明性概率编程语言

“我的生活”系列的最后一集仍在筹备中，但我需要用一些激动人心的消息打断这部系列剧。我在过去一年左右一直致力于的新编程语言刚刚在我们的论文Bean Machine的出版中公布：一种用于高效可编程推理的声明性概率编程语言。

在我进入细节之前，有几个关于在到期的地方归功的注意事项，诸如此类：

虽然我的名字出现在纸上是出于礼貌，但这篇论文不是我写的。特别感谢并祝贺纳兹·特赫拉尼和尼姆·阿罗拉，他们为撰写这篇论文做了大量工作。

我每天工作的语言基础设施的实际部分是一个研究项目，涉及Bean Machine程序底层的贝叶斯网络的提取、类型分析和优化。我们还没有宣布该项目的细节，但我希望不久就能在这里讨论这个问题。

现在我们只有报纸；更多关于这种语言的信息以及如何自己拿出来兜风的信息稍后会公布。它会在准备好的时候发货，这就是我掌握的所有日程信息。

语言的名称来自一种用于可视化概率分布的物理设备，因为它就是这样做的。

我可能会在今年秋天晚些时候做一个关于豆子机器的整个系列，但今天让我给你简要的概述，如果你不想浏览这篇论文的话。正如论文标题所说，Bean Machine是一种概率编程语言(PPL)。

有关ppls的详细介绍，您应该阅读我的“修复随机”系列，在该系列中，我展示了如何通过向基类库添加类型和向C#等语言添加语言功能来极大地提高对.NET中随机性分析的支持。

如果你不想读那篇40多篇的介绍，这里是TLDR。

我们都习惯了两种基本的编程：产生效果和计算结果。需要理解的重要一点是，Bean Machine坚定地站在“计算结果”阵营。在我们的PPL中，程序员的目标是声明性地描述世界如何工作的模型，然后在模型的上下文中输入对现实世界的一些观察，并让程序在给定这些观察的情况下产生真实世界可能是什么样子的后验分布。它是一种用于编写统计模型模拟的语言。

一个“hello world”示例可能会有所帮助。让我们回顾一下我在“修复随机”第30部分中第一次讨论的场景：抛出一枚来自不公平造币厂的硬币。也就是说，当你从这个铸币厂抛出一枚硬币时，你不一定有50-50的机会得到正面和反面。然而，我们确实知道，当我们铸造一枚硬币时，公平的分配是这样的：

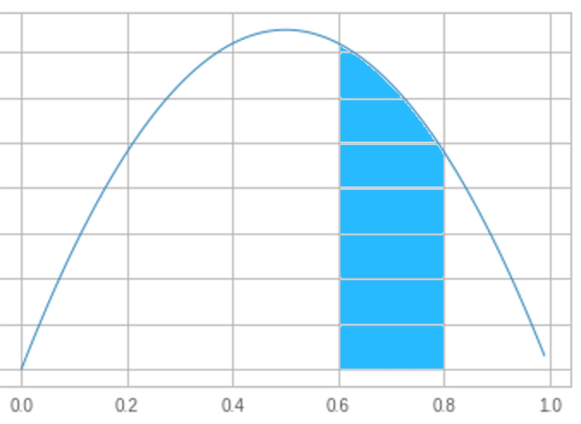
公平是沿着x轴的；0.0表示“总是尾巴”，1.0表示“总是正面”。获得特定公平的硬币的概率与图下的面积成正比。在上面的图表中，我突出显示了0.6到0.8之间的区域；蓝色区域大约占曲线下总面积的25%，所以我们有25%的机会将硬币放在0.6到0.8之间。

同样，0.4到0.6之间的面积约占总面积的30%，所以我们有30%的机会得到一枚公平性在0.4到0.6之间的硬币。我敢肯定你看到这是怎么回事了。

假设我们铸造了一枚硬币，我们不知道它真正的公平，只知道上面公平的分配。我们把硬币抛100次，得到72个正面，28个反面。这枚硬币最可能的公平性是多少？

显然，100次中出现72次正面的硬币最有可能的公平性是0.72，对吗？

嗯，不，不一定是对的。为什么？因为我们得到一枚介于0.0和0.6之间的硬币的先验概率，比我们得到一枚介于0.6和1.0之间的硬币的先验概率要高得多。纯粹靠运气，100个硬币中有72个头是可能的，硬币的公平性在0.0到0.6之间，而且这些硬币总体上更有可能。

旁白：如果这一点不清楚，试着想一想我在上一系列文章中讨论的一个更简单的问题。你有999枚公平硬币和一枚双面硬币。你随便挑一枚硬币，掷十次，就会得到十个头。最可能的公平性是0.5还是1.0？换句话说，你得到双面硬币的概率是多少？很明显，它不是之前的0.1%，但也不是100%；你可以用一枚公平的硬币幸运地一连得到10个人头。考虑到这些观察结果，选择双头硬币的真实后验概率是多少？

我们在这里要做的是在两个相互竞争的事实之间取得平衡。首先，我们观察到一些掷硬币最符合0.72公正性的事实，其次，硬币可以很容易地变小(或变大！)。公平地说，我们幸运地得到了72个人头。为了计算出可能公平的真实分配，进行这种平衡行动的数学方法绝不是显而易见的。

我们想要做的是使用像Bean Machine这样的PPL来为我们回答这个问题，所以让我们构建一个模型！

代码可能看起来非常熟悉，这是因为Bean Machine是一种基于Python的声明性语言；所有Bean Machine程序也都是合法的Python程序。我们先说一下我们的“随机变量”是什么。

旁白：统计学家使用“变量”的方式与计算机程序员非常不同，所以不要被你的直觉所蒙蔽。我们所说的“随机变量”是指我们有一个可能的随机值的分布；从分布中提取的这些值中的任何一个的表示都是“随机变量”。

为了表示随机变量，我们声明一个函数，该函数返回从中提取随机变量的分布的pytorch分布对象。上面的曲线由函数beta(2，2)表示，我们有一个对象的构造函数来表示我们正在使用的pytorch库中的分布，因此：

就这么简单。Coin()程序中的每一次使用在逻辑上都是单个随机变量；该随机变量是通过从上图的beta(2，2)分布中对其进行采样而生成的硬币公平性。

旁白：代码看起来可能有点奇怪，但请记住，我们在C#中一直都在做这样的恶作剧。在C#中，我们可能有一个方法看起来返回一个int，但是返回类型是Task<；int>；；我们可能有一个方法Year返回一个Double，但是返回类型是IEnumerable<；Double>；。这非常相似；该方法看起来像是返回公平性的分布，但从逻辑上讲，我们将其视为从该分布中提取的特定公平性。

然后我们该怎么办呢？我们抛硬币100次。因此，我们需要为每一次抛硬币提供一个随机变量：

我们来分析一下。每个调用flip(0)、flip(1)等等都是不同的随机变量；它们是Bernoulli过程-“抛硬币”过程-的结果，其中硬币的公平性由单个随机变量Coin()给出。但是，每次调用flip(0)在逻辑上都是相同的特定硬币抛出，无论它在程序中出现了多少次。

出于本练习的目的，我生成了一枚硬币，并模拟了100次投掷硬币，以模拟我们对现实世界的观察。我有72个头。因为我可以在幕后偷看这个测试的目的，我可以告诉你硬币的真正公平性是0.75，但当然在现实世界的情况下我们不会知道这一点。(当然，用一枚0.75枚公平的硬币在100枚硬币上掷出72个人头是完全有可能的。)。

我们需要说一说我们的观测结果是什么。在pytorch中的伯努利分布产生了一个1.0的“头”张量和一个0.0的“尾”张量。我们的观测被表示为从随机变量到观测值的字典映射。

Heads=张量(1.0) 尾部=张量(0.0) 观测值={ 翻转(0)=头部， 翻转(1)=尾部， ..。以此类推，100次，72个头，28个尾。 }。

最后，我们必须告诉Bean Machine要推断什么。我们想知道硬币公平的后验概率，所以我们列出了我们想要推断后验的随机变量的列表；在这种情况下只有一个。

在给定这些观测的情况下，我们从硬币的后部公平性中得到一个表示样本的对象。(为清楚起见，我在这里将调用地点略微简化为推理方法；它需要更多参数来控制推理过程的细节。)。

返回的“公平性”对象是有效模拟可能的世界的结果，这些可能的世界会将您带到观察到的头部和尾部；然后，我们有一些方法允许您使用标准绘图包来绘制这些模拟的结果：

橙色标记是我们最初对观察到的公平性的猜测：0.72。红色标记是用于生成观察值的硬币的实际公平性，0.75。蓝色直方图显示了1,000个模拟的结果；产生那72个头的绝大多数模拟的公平性在0.6到0.8之间，尽管造币厂生产的硬币只有25%在这个范围内，但正如我们所希望的那样，橙色和红色的标记都在直方图的峰值附近。

所以，是的，0.72接近最可能的公平，但我们在这里也看到了很多其他公平的可能性，而且，我们清楚地看到它们与0.72相比的可能性有多大。例如，0.65也是很有可能的，而且它比比如说0.85更有可能。这应该是有道理的，因为先前的分布是，接近0.5的公平性比更远的公平性更有可能；左边的直方图比右边的直方图有更多的“块状”：这是先前对后方的影响！

当然，因为我们只做了1000次模拟，所以有一些噪音；如果我们做更多的模拟，我们会得到更平滑的结果和清晰的单峰。但是对于一个只需要几秒钟就能运行的6行模型代码的Python程序来说，这是一个相当好的估计。

我们为什么要关心掷硬币呢？显然，我们并不关心为了自己的利益而解决掷硬币的问题。相反，在现实世界中，有大量的问题可以被建模为抛硬币，即“造币厂”生产不公平的硬币，我们知道来自造币厂的硬币的分配情况：

一家工厂生产的路由器具有一定的“可靠性”；通过网络中的每个路由器的每个数据包都以这种可靠性“掷硬币”；头，包被正确发送，包的尾不正确。根据实际数据中心的观察，哪台路由器最有可能出现故障？我在我的“修复随机”系列中描述了这个模型。

人类评论家将照片归类为“一张有趣的猫照片”或“不是一张有趣的猫照片”。我们有一个照片来源-我们的“薄荷糖”-产生的照片有一定的概率是有趣的猫照片，我们有人类审查员，每个人都有一定的分类错误概率。给出一张照片和来自十位评论家的十个分类，这是一张搞笑的猫照片的可能性有多大？同样，这些动作中的每一个都可以建模为抛硬币。

新用户可能是真人，也可能是怀有敌意的机器人。新用户向您发送好友请求；您可以根据个人接受好友请求的可能性接受或拒绝该请求。这些动作中的每一个都可以建模为抛硬币；给出对所有这些“抛硬币”的一些观察，账户是敌意机器人的后验概率是多少？

以此类推；我们可以通过建立抛硬币模型来解决大量现实世界的问题，而Bean Machine做的不仅仅是抛硬币模型！

我知道这很难理解，但并不是每天都要用一种全新的编程语言来解释！在以后的几期节目中，我将更多地讨论Bean Machine是如何在幕后工作的，我们是如何在声明性和命令性风格之间进行权衡的，诸如此类的事情。到目前为止，这是一次令人着迷的旅程，我迫不及待地想分享它。