塔勒布对智商的看法是错误的(2019年)

在这篇文章中，我研究了纳西姆·塔勒布(Nassim Taleb)的这份文件：智商在很大程度上是一个伪科学的骗局。这份文件的大部分内容只是夸夸其谈，但他确实提出了一些量化的主张，这是好的。我用真实数据调查了这些说法的真实性。

[编辑：下面的引述是从塔勒布的文档中逐字摘录的，因为这篇文章是在上传时写的。]。

我已经在这里准备了WLS数据集，它有很好的智商测试，所以我将使用它。让我们来看看智商成绩的回归。

Wls<；-read_feather("；data/wls.f"；)%>；% 筛选器(rtype=="；g"；)%>；% 变异(GRADES_STD=比例(等级)) 汇总(lm(GRADES_STD~IQ_STD，WLS%>；%DROP_NA(IQ_STD，GRADES)。

调整后的R2为0.356，所以智商可以解释这个数据集中年级方差的~35%。塔勒布的捍卫者可能会说，像学校成绩这样的事情在现实生活中并不重要。但不管你对此持什么立场，情况是他对智商最多只能解释多少做出了具体的声明，这与一个很大的因素有出入。

结果显示，在最好的应用程序中，智商比随机选择高出不到6%。

他没有具体说明他这么说到底是什么意思。但我非常肯定他正在考虑一个类似他在这条推文中谈到的比较：

所以我将分析一些东西，一个带有类似于这些假设的风格化的例子。在现实世界中，你可能会有其他使情况变得复杂的信息，比如教育背景；但我们目前忽略这些信息。

我创建了两个正态分布变量，相关系数为0.5，并将其命名为IQ和Performance。

N<；-10**8 X0<；-MASS：：mvrnorm( N=n， µ=c(0，0)， σ=矩阵(c(1，0.5，0.5，1)， 2，2) DF<；-Tibble(IQ=X0[，1]， 性能=X0[，2]) Df%>；%汇总(%摘要) COR=COR(智商，性能)， N=n()， Mean_IQ=Mean(IQ)， SD_IQ=SD(IQ)， Mean_Performance=Mean(性能)， SD_PERFORMANCE=SD(性能) )。

如果您雇用的员工智商高于平均水平，则聘用绩效高于平均水平的员工的概率为：

如果有0相关性的概率当然是0.5。因此，使用智商作为标准比随机选择高出16.67%(塔勒布也发现了这一点)。这是略高于6%，但这是一个细节。更重要的是，这个例子是一个理论上的用例，其中使用智商测试并不是很有用。为了看一些更现实的东西，假设一家公司想要避免业绩低于平均值2个标准差以上的员工。(也许这类员工有造成巨大伤害的风险，例如，这可能是军队中的一个问题。)。我们再次比较了随机录取和只录取智商高于平均水平的申请者。

如果公司随机录取员工，我们得到的是绩效低于平均值2 SD以上的人的比例：

如果公司只接受智商高于平均水平的申请者，我们得到的是表现低于平均水平2 SD以上的人的比例：

换句话说，在这种情况下，使用智商选择标准比随机选择要高出450%以上。与声称的6%相差甚远。

图片来源于本文，数据来源于NLSY79。这些数据也是公开的，所以我们可以再检查一次。这里描述了我执行的预处理过程。

该图看起来与论文中的类似，但略有不同，因为我使用的是10年的平均收入值，而不是某一年的平均收入值。

Sc<；-scale_y_Continuity( 中断=c(100000,200000,300000,400000,500000)， 标签=c("；$100,000&34；，"；$200,000"；，"；$300,000"；，"；$400,000"；，"；$500,000"；) ) NLSY%>；%gglot(AES(x=IQ，y=收入))+ Geom_point(alpha=1，大小=0.5)+sc。

正如塔勒布使用的情节一样，很难看出所有的覆盖点都发生了什么。降低透明度在一定程度上有所帮助。

NLSY%>；%gglot(AES(x=IQ，y=收入))+ Geom_point(alpha=0.2，大小=0.5)+sc。

如果我们只看年收入在45.000美元以上，仍然有大约0.3%的明显相关性。

另一种使这种关系更清晰的方法是绘制不同智商群体的收入分配图。绘制分布图避免了由于重叠点导致绘图变得不清楚和混乱的问题。

下面的图表同样只显示年收入超过45000美元的人。智商的不同很明显，无论是在中位数上，还是在尾巴的长度上。

NLSY_g<；-NLSY%>；%Drop_NA(收入，智商)%>；% 变异( IQ_GROUP=FACTOR(CASE_WHEN( 智商=80~#34；<；80"；， 在(IQ，80，90)~"；80-90&34；之间， 在(IQ，90,100)~"；90-100"；之间， 介于(IQ，100,110)~"；100-110"之间；， 在(IQ，110,120)~"；110-120"；之间， 智商=120~#34；>；120&34；)， 级别=c("；>；120&34；、"；110-120&34；、"；100-110&34；、"；90-100&34；、"；80-90&34；、"；<；80"；)) ) NLSY_G%>；%筛选器(收入>；45000)%>；% PLOT_RIDGES_Q("；收入"；，"；IQ_GROUP"；)+ SCALE_x_CONTINUATION( 极限=c(20000,200000)， 中断=c(50000,100000,150000,200000)， 标签=c("；$50,000&34；，"；$100,000"；，"；$150,000"；，"；$200,000"；))

(收入数据)截断了大的上行空间，因此我们甚至看不到厚尾的影响。

正确的是，在存在厚尾的情况下，这种相关性在预测预期收入时是不具信息性的。而来自这些研究的数据并没有提供关于这些尾巴的良好信息。然而，智商的影响很可能对尾巴的影响更大，而不是更小。例如，比尔·盖茨和保罗·艾伦在他们的SAT考试中得了1590分/1600分，这在当时对SAT来说意味着极高的智商。由于比尔·盖茨也是财富和收入的尾巴，这表明尾巴上的人的总体影响是强调而不是削弱智商的重要性。

他声称，智商与低智商时的特征高度相关，但当智商高于中位数时，这种相关性就会急剧下降，就像帖子中的这个数字所示：

(编辑：如果这一点不清楚，Taleb使用上面的数字作为说明，而不是作为精确的经验主张。)。很容易查看数据，看看情况是否真的如此。我们可以使用上面使用的两个相同的数据集。

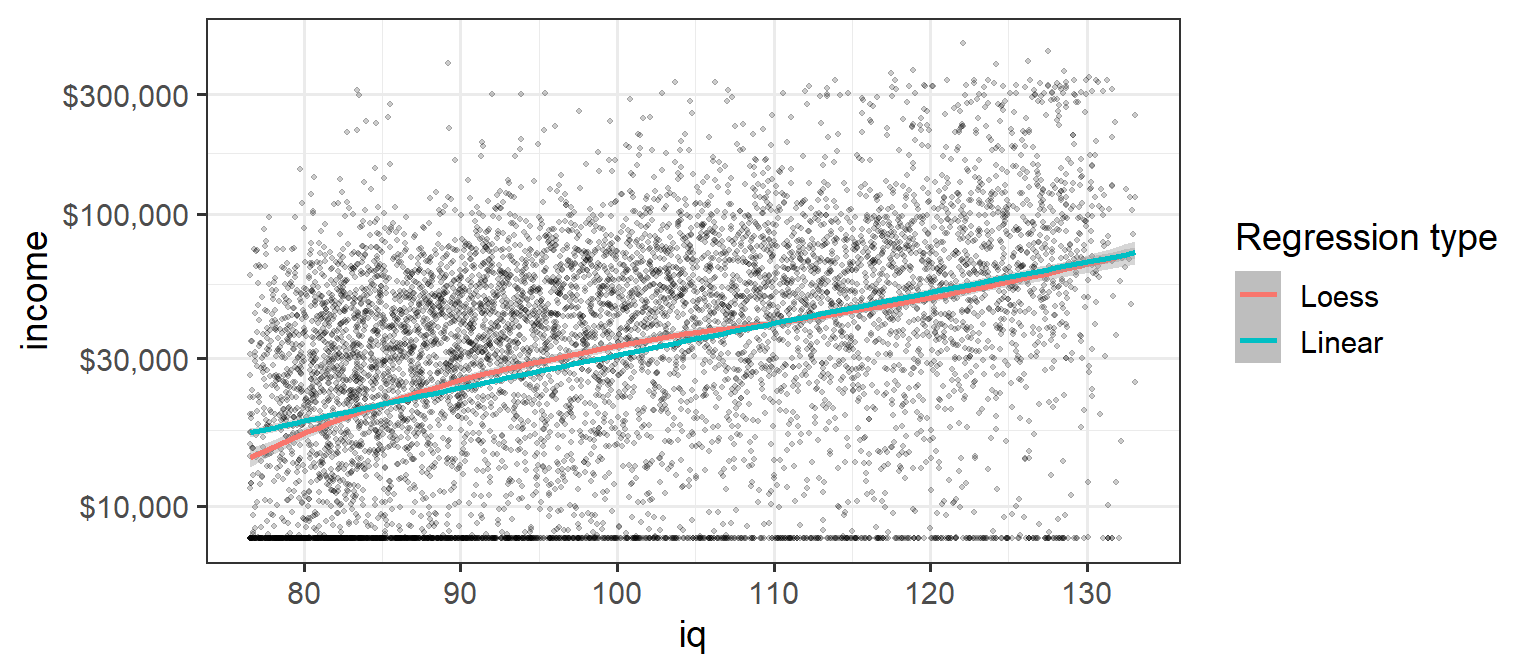
如果我们绘制IQ与log(收入)的曲线图，这将告诉我们每个额外的IQ点带来的收入增加的百分比有多大。然后，我们可以绘制局部回归图(黄土)，并将其与线性回归进行比较。如果智商和收入之间的关系在高于平均智商的情况下从根本上减弱，那么我们预计黄土回归线将接近水平。然而，这并不是我们所看到的-相反，两条回归线彼此紧随其后。诚然，智商较低的人每个智商点数的收入增长百分比会稍高一些，但从不会停滞不前。

NLSY%>；% Gglot(AES(x=IQ，y=收入))+ GEOM_POINT(Alpha=0.2，大小=0.8)+ STAT_Smooth(AES(COLOR="；蓝色"；)，方法="；黄土"；)+ STAT_Smooth(AES(color="；绿松石4"；)，method="；lm"；)+ SCALE_COLOR_DISPLATION( 名称="；回归类型"；， 标签=c("；黄土"；，"；线性"；))+ SCALE_Y_CONTINUATION( 交易="；log10"；， 中断=c(10000,30000,100000,300000)， 标签=c("；$10,000&34；，"；$30,000"；，"；$100,000"；，"；$300,000"；)+ Coord_transs(y="；log10"；)。

Plot_Smooth<；-函数(df，Over_Medium，COLOR){ STAT_Smooth(AES(COLOR=COLOR)，DATA=DF%>；%过滤器(IQ_OB上方_中值==OB上方_中值)， 方法="；lm"；，Se=F，Fill=NA，公式=y~x，大小=1.2) } WLS%<；>；%突变(IQ_OVER_MENTAL=iq100>；100) Wls%>；百分比 GGPLOT(AES(y=成绩，x=iq100))+ Geom_Jitter(Alpha=0.05)+ Plot_Smooth(WLS，F，"；绿松石4"；)+ Plot_Smooth(WLS，T，"；蓝色"；)+ SCALE_COLOR_DISPLATION( 姓名="；人际关系、智商和成绩"；， 标签=c(高于智商中位数34；，低于智商中位数34；))+ 实验室(x="；智商(IQ"；)。

我们清楚地看到，100以上的IQ线有一个不是水平的斜率，这意味着IQ与成绩相关，即使在IQ中值更高的情况下也是如此。事实上，这个斜率与智商中位数以下学生的回归线大致相同。

在第三个例子中，我们可以看到高智商、低智商和中智商的收入分布。智商的提高都会移动收入分配的中位数，并扩大尾部。

NLSY_g<；-NLSY%>；%Drop_NA(收入，智商)%>；% 变异(IQ_GROUP=因子(CASE_WHEN( 智商=85~#34；<；85"；， 在(IQ，95,105)~"；95-105"；之间， IQ>；115~#34；&>115&34；)， 级别=c("；>；115"；，"；95-105&34；，"；<；85"；)) )%>；% DROP_NA(IQ_GROUP) NLSY_g%>；% PLOT_RIDGES_Q("；收入"；，"；IQ_GROUP"；)+ SCALE_x_CONTINUATION( 极限=c(-20000,210000)， 中断=c(0,50000,100000,150000,200000)， 标签=c("；0"；，"；$50,000&34；，"；$100,000"；，"；$150,000"；，"；$200,000"；))。

我看过的这篇文章中的所有主张，都可以被解释为具体的东西，并在真实的数据集中进行测试，结果证明是不正确的。如果Taleb没有屏蔽所有与他意见不同的人，也许他就会发现这一点，而不会发布一篇带有所有这些不正确说法的帖子。