用于矩阵处理的光学元件
在我们之前的博客文章中,我们介绍了使用硅光子学来执行大规模线性算术运算的想法,其速度和效率比使用数字电子技术更快、更高效。您可能还记得,我们的系统使用许多称为马赫-曾德尔干涉仪(MZI)[1]的相同器件来实现基本的线性运算,即2x2矩阵乘法,由此可以构建更大的矩阵乘法。在这篇博客文章中,我们的目标是更详细地描述MZI是如何工作的,并希望阐明硅光子学相对于数字电子学在执行算术方面的一些优势。
我们首先考虑可用于标量乘法的MZI。基本布局如下所示。单输入波导对称分裂成干涉仪的两臂。当光沿着每一臂行进时,电磁波在被重新组合成单个输出波导之前,会拾取一个(通常)依赖于路径的相位。我们将此配置称为“标量MZI”。
标量MZI可以分为三个部分:两个Y结和一个差分相移。在对整个系统进行分析之前,让我们先了解一下这些子系统。
Y结是具有单个端口(A)的3端口集成光学器件,它平等地耦合到一对端口(B和C)。一个简单的版本可以通过将直波导连接到左转和右转波导弯头来实现,如下所示。
当将光送入端口A时,光信号经历如下传输矩阵所描述的变换:
为了得到输出波导模式(B和C)的光场振幅,我们可以将输入场振幅乘以传输矩阵。假设输入振幅为1,我们获得相同的输出场振幅:
不出所料,端口A的输入光被简单地一分为二,每个输出波导中都有一半的光功率(光功率与场幅的平方成正比)。在这种情况下,灯光的行为非常类似于管道系统中的水。
现在让我们检查一下当我们在端口B输入光时会发生什么。通过光学互易性(光学中的一种原理,即光可以沿着同一路径双向传播--想想您眼镜的镜片),反向通过它的传输矩阵仅仅是正向传输矩阵的转置:
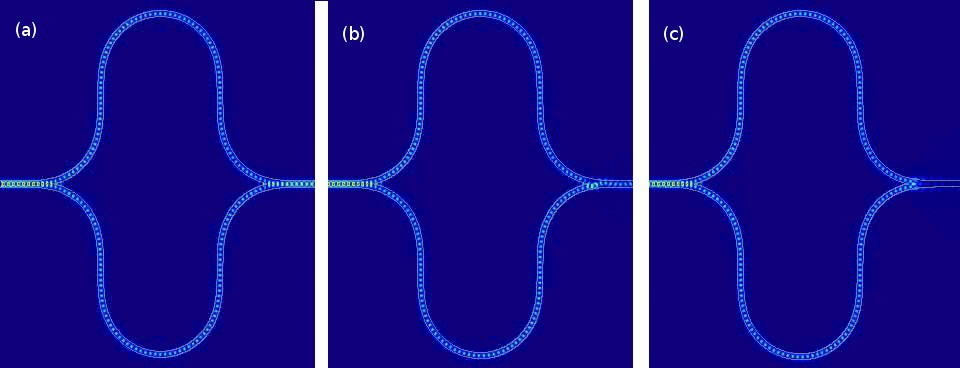
请注意,只有一半的输入功率到达了输出,其余的似乎魔术般地消失了(实际上它是从系统中辐射出来的)。在这种情况下,灯光的波动性质使其行为与经典流体(管道中的水)不同,如下面的模拟所示。
现在让我们考虑最后一种情况,在这种情况下,光同时发射到端口B和端口C。在这种情况下,我们可以将输入场振幅分别任意设置为b和c。同样,我们将输入幅度向量乘以传输矩阵,以得到:
这个最终的Y结结果说明了光学中一个称为叠加的基本概念:系统对多个激发源的响应就是对每个单独源的响应的总和(或叠加)。这是光学执行线性算术的主要优点之一:作为系统固有线性的直接结果,加法就像组合(例如干涉)两个光学模式一样简单。此外,加法操作实际上是免费的:不需要功耗!请注意,输入光的生成确实需要功耗,但这不应包括在加法操作的成本中,正如本文在接近尾声时所讨论的那样。
没有差分相移部分的标量MZI是将所有输入光传输到输出的无用器件。在算术运算方面,它可以被认为是将一个数字分成相等的两个部分,然后再将这两个一半相加在一起。然而,正如我们将看到的,在两个臂之间引入相移导致传输到输出模式的光功率改变。相移部分的传输矩阵可以写成:
在两个手臂之间引入相位差的方法有很多种,但它们基本上都是基于延迟一条手臂相对于另一条手臂的波前。
也许最简单的方法是制作不同长度的手臂。因为每个臂中的波以相同的速度传播,所以较长臂中的波相对于较短臂中的波会延迟,从而产生相对相位差:
其中n是波导的折射率,ΔL是两臂之间的长度差,λ是光的自由空间波长。
系统的传输矩阵是通过将各组成部分的传输矩阵相乘得到的(令人困惑的是,假设光从左到右传播,传输矩阵以与元素相反的空间顺序写出)。因此,标量MZI的合成转移矩阵可以计算为:
因此,标量MZI的输出仅仅是其输入乘以标量值(cos(φ))。这说明了线性算术所需的第二个关键功能:标量乘法。再说一次,就像加法一样,使用光学进行标量乘法不需要耗散能量!
可编程相移通常依赖于改变引导材料中的波速,即其折射率,而不是依赖于光路长度。根据相关材料的不同,有几种常见的方法来实现这一点。这些效应包括热光效应,其中材料的折射率随温度变化;等离子体色散效应,其中半导体的准费米能级(电子和空穴的浓度)改变其折射率;以及电光效应,其中向材料施加电场会引起其折射率成比例的变化。在热光效应中,材料的折射率随温度而变化;等离子体色散效应,其中半导体的准费米能级(电子和空穴的浓度)改变其折射率;以及电光效应,其中向材料施加电场会导致其折射率成比例变化。使用上述效果中的任何一种都能够实现可编程相位差。
现在让我们考虑一个具体的例子:假设相位差部分中的波导是由电光材料制成的。在这种情况下,可以使用施加在每个臂上的相反电场来诱导臂之间的差分相位。这些电场可以在单个电压下获得,如下图所示。
其中c是材料的电光系数,d是电极之间的距离,L是电光部分的长度,λ是光的自由空间波长。对于输入场幅度A,MZI的输出场幅度由下式给出:
从这个例子中我们可以看到,由MZI实现的标量乘法器可以被编码成电压。这一点很重要,因为它允许使用高速电子设备对电光乘法器的值进行编程,从而实现完全集成的可重构解决方案。虽然改变乘数值需要电荷通过电势传输并因此需要能量耗散,但是如果在这种情况下电光材料是不导电的,则保持静态乘数值不需要。
现在我们已经了解了如何使用“标量MZI”进行标量乘法,现在我们将把它修改为“向量MZI”来执行矩阵-向量乘法。原理图版本如下所示:
同样,我们可以将系统分成3个子部分,但这次我们用50:50的定向耦合器取代了y形结。
定向耦合器是具有两对端口(A/B和C/D)的4端口集成光学器件。一对中的每个端口都耦合到另一对中的两个端口,但不耦合到其伙伴。因此,例如,如果光输入到端口A和B,则端口C和D的输出幅度将分别是输入幅度的线性组合。这样的器件是通过将两个波导拉近以使它们彼此渐变耦合来实现的,如下所示:
无损定向耦合器的一种形式可以由2x2么正传递矩阵表示:
与标量MZI的情况一样,我们可以通过将子组件的传递矩阵按正确的顺序相乘来获得系统的传递矩阵:
请注意,在这种情况下,结果矩阵是2x2,而不是标量版本中的1x1。与其组件定向耦合器非常相似,输出场幅度是输入场幅度的线性组合;实际上,将矢量MZI视为可编程定向耦合器是正确的。该设备的算术运算是将输入幅度向量与其传递矩阵相同地相乘。正如许多读者会从线性代数入门课程中回忆起的那样,矩阵乘法只是一系列有组织的标量乘法和加法:这两种基本运算我们已经确定在电光电路中是无能量的。毫不奇怪,这种复合操作也可以在零功耗的情况下执行。
通过将矢量和标量MZI与简单的移相器串联到合适的网络中,可以实现任意矩阵乘法,并且可以在不消耗任何功率的情况下执行乘法。应当注意,有必要消耗网络的输入和输出处的功率来编码输入向量(这包括光产生),并解码输出向量。然而,将N×N矩阵乘以N×1矢量只需要O{N}个编码/解码操作,而需要O{N²}个标量乘法和加法。数字电子需要耗散能量来执行标量乘法和加法。从光学领域所需的耗能操作的可伸缩性大大降低的情况来看,应该清楚地看到,当N&gT;α;α时,光学设备的效率总是更高的,这是有价值的。
LightMatter的一个挑战是设计我们的系统,既要降低α的值,又要增加N的值,以便我们可以为其构建实际的系统。通过降低α的价值,我们将拓宽光计算具有吸引力的应用范围,并提高我们在降低与计算相关的能源成本方面的影响力。通过增加N的可达值,我们将尽我们的一份力量来扩展人类能力的范围,使计算能够达到常规数字机器无法实现的规模!