在多人游戏的版图中导航

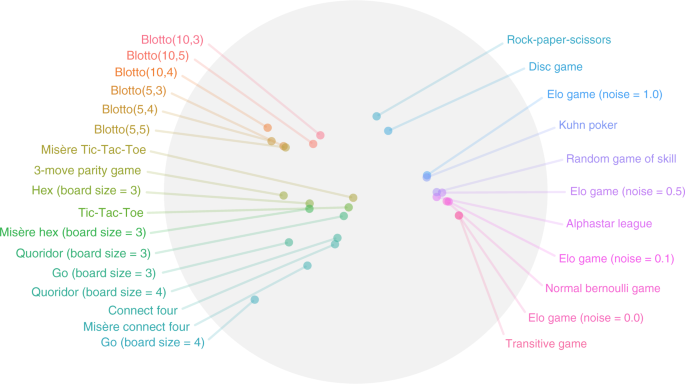
多人游戏长期以来一直被用作人工智能研究的试验床，被恰当地称为人工智能中的果蝇。传统上，研究人员一直专注于使用知名游戏来构建强大的代理。然而，通过描述游戏及其拓扑结构，可以更好地了解这一进展。解决后一个问题可以促进对代理人的理解，并有助于确定代理人下一步应该以什么游戏为目标，作为其培训的一部分。在这里，我们展示了如何将网络测量应用于大型游戏的响应图，从而创建游戏景观，量化不同大小和特征的游戏之间的关系。我们在从规范博弈到复杂的经验博弈等领域阐述了我们的发现，捕捉了训练有素的代理人相互竞争的表现。我们的结果在一个示范中达到顶峰，利用这些信息产生新的有趣的游戏，包括从现实世界游戏中合成的经验游戏的混合。

游戏在开发学习算法和衡量人工智能(AI)1、2、3、4的进展方面发挥了重要作用。尤其是多人游戏在AI研究中发挥了关键作用，并在机器学习中得到了广泛的研究，从博弈论中的抽象基准，到流行的棋类游戏，如国际象棋5、6和围棋7(被称为AI Research 8中的果蝇)，到实时战略游戏，如StarCraft II 9和Dota 2 10。总的来说，AI研究主要侧重于。我们把这称为政策问题，这需要寻找超人水平的人工智能性能。尽管取得了这一进展，但近年来11、12对任务理论(对AI任务进行分类、表征和分解的框架)的需求变得越来越重要。自然，理解游戏空间的技术可能有利于未来AI实体12、13的算法开发。理解和分解游戏的表征特征可以通过课程学习14被用于代理的下游训练，该课程学习14寻求使代理能够学习日益复杂的任务。

与设计这样的任务理论相关的核心挑战最近被称为问题问题，被定义为“生成大量有趣的自适应环境以支持研究的工程问题”15。与问题问题相关的研究有30多年的丰富历史，包括前述关于任务理论11、12、16、程序化生成的视频游戏特征17、18、19、用于一般游戏的游戏和规则集的生成20、21、22、23、24、25、26以及程序性内容生成技术27、28、29、30的工作。我们请读者参阅补充说明1，以详细讨论这些和相关工作。其中几个相互关联的领域背后的一个重要问题是：是什么让游戏变得足够有趣，让人工智能特工学会玩？解决这一问题需要能够刻画游戏拓扑结构的技术，这是本文感兴趣的主题。我们特别关注多人游戏(即涉及多个代理相互作用的游戏)的特征，此后使用游戏的简写来指代这一类。

本文的目标是建立工具，使人们能够发现游戏上的拓扑，无论它们是否有趣；我们在这里并不寻求回答有趣的问题，尽管这样的工具包可能对后续的研究有用。当然，从以人为本的游戏设计、发展性学习、课程学习、人工智能培训等角度来看，游戏有趣的原因有很多。我们后来的实验与查内斯基等人最近的工作联系在一起。37，它专门从人工智能训练的角度调查了让游戏变得有趣的属性，这里也考虑到了这一点。我们遵循了查内斯基等人的趣味性特征。37，它定义了所谓的技能游戏，吸引经纪人的原因是：(I)进步的概念；(Ii)表现类似的多样化游戏风格的可用性。稍后，我们将展示通过我们的方法发现的游戏集群是如何与这种趣味性概念相一致的。我们方法的一个重要好处是它同样适用于对抗性博弈和合作性博弈。此外，虽然由于那些特定实验中选择的支付参数，我们稍后给出的程序博弈结构生成结果是目标零和博弈，但它们很容易扩展到一般和博弈。

如何从拓扑上分析游戏呢？人们可以认为游戏的特征是通过可用策略的数量、参与的玩家等度量来量化的

我们开发了一个基本的图论工具包，它有助于分析规范和大规模的游戏，提供对它们的相关拓扑结构的洞察，根据它们的高层战略互动。前提博弈论背景和技术细节在“方法”一节中提供，相关工作和补充说明1中对相关工作进行了充分讨论。

我们的研究结果总结如下。我们使用我们的工具包来描述一些游戏的特征，首先分析具有良好定义的结构的激励例子和规范游戏，然后扩展到更大规模的经验游戏数据集。对于这些较大的游戏，我们依赖经验博弈论分析67，68，其中我们使用一组样本政策来描述潜在的游戏。虽然经验博弈论结果受到用于生成这些结果的政策的制约，但我们依赖于设计的抽样方案，该方案旨在捕获每个游戏中的各种交互，并随后进行敏感性分析，以验证结果的稳健性。我们论证了与博弈相关的图的复杂性与求解博弈本身的复杂性之间的相关性。在补充说明2中，我们对照2个 × 2游戏的分类基线方法对我们提出的方法进行了评估38。最后，我们演示了这个工具包如何被用来自动生成有趣的游戏结构，例如，这些结构可以随后用于训练AI代理。

让我们从一个鼓舞人心的例子开始，以巩固直觉，并解释我们的图论工具包的工作流程，使用在玩家收益中具有简单参数结构的游戏类。具体地说，考虑三大类游戏(如补充方法1中详细描述的那样)：策略具有明确的传递顺序的游戏(图2a)；策略具有循环结构的游戏，其中除最终策略外，所有策略都是相互传递的(图2d)；以及具有随机(或没有明确的底层)结构的游戏(图2g)。我们将看到，通过所提出的分析，具有共享底层结构的游戏的核心特征被恢复。

A、d和g分别可视化具有传递、循环和随机结构的博弈实例的收益。每个示例游戏由两个玩家组成，每个玩家有10个策略(带有支付行和列标签，{s 0，…。，(9)，指示策略)。尽管在所示的每类博弈中可能存在许多收益变化，但每一类博弈都共享分别在b、e和h中所示的基础收益结构。此外，收益的变化可以显著地影响这些博弈的求解难度(即，找到纳什均衡)，如c，f，i中所示。

这些图中的每一个都可视化对应于相应类别的游戏的4个实例的收益，每个游戏涉及每个玩家10个策略；更具体地，如果玩家分别使用策略si和sj(分别对应于每个赢利表的第i和j行和列)，则图2a、d和g中可视化的每个矩阵的条目M(si，sj)量化了第一个玩家收到的收益。尽管在这里例举的游戏实例中收益的差异很明显，但每个游戏本质上共享通过分别在图2b、e和h中重新排序其策略而暴露的收益结构。换句话说，后一组图中的收益的可视表示简明地表征了这些游戏类别内的战略交互的主干，尽管在可视化的各个实例中不是立即明显的。

更重要的是，在这些游戏中学习有用的混合策略的复杂性与这种结构性支柱密切相关。为了举例说明这一点，考虑求解每一个博弈的计算复杂性；为了简洁，我们此后将求解博弈称为寻找纳什均衡的同义词(类似于先前的工作69、70、71、72，其中纳什均衡是感兴趣的解概念)。具体地说，我们通过使用双重Oracle算法73来可视化这种计算复杂性，该算法在多智能体和博弈论文献47、74、75、76中已被公认为纳什求解器。在较高层次上，双甲骨文从由单个随机选择的策略组成的子博弈开始，通过最佳响应(由甲骨文计算)迭代地扩展策略空间，直到发现整个底层博弈的纳什均衡。

图2c，f和i可视化了在随机初始化下求解相应游戏所需的双重Oracle迭代的分布。特别要注意的是，尽管图2a，d中分别可见的传递博弈和周期性博弈的基本收益结构是相似的，但在图2a，d中引入了循环

在给定博弈收益a的情况下，博弈的所谓α-Rank响应图在b中可视化。在c中，通过使用图拉普拉斯的顶部特征向量来重新投影响应图产生谱响应图，其中类似的策略被放置在彼此接近的位置。在d中，进一步进行这一步，可以对频谱响应图进行群集，从而产生群集响应图，该群集响应图在该特定示例中暴露了三类策略。在e中，通过融合每个集群内的节点来收缩集群图产生了可传递博弈的高级特征。在f中，这类传递对策的圈的缺失是显而易见的。最后，在g和h中，可以提取各种响应图统计的主成分，并建立到过程性游戏结构生成方案的反馈回路，以产生新的游戏。

通过将游戏表示为图形，可以对游戏的底层结构和复杂性提供各种有用的见解。例如，考虑图中的圈的分布，其在多智能体评估和训练方案41、50、53、77中扮演重要角色，并且如稍后所示，与求解两人零和博弈的计算复杂性相关(例如，通过双Oracle)。图3f清楚地表明，在这类特定的传递游戏中缺乏循环；虽然这在图3a的基础(全序)回报可视化中很明显，但在图3a中看到的无序变体中就不那么明显了。即便如此，通过对底层游戏响应图进行频谱分析，策略之间的高层关系结构变得更加明显。此过程的完整技术细节在“方法”一节中提供。在较高级别，图的所谓拉普拉斯谱(即，特征值)连同相关联的特征向量一起捕获关于它的重要信息(例如，生成树的数量、代数连通性和许多相关属性78)。通过使用顶部特征向量重新投影响应图产生图3c中可视化的光谱响应图，其中类似的策略被放置在彼此接近的位置。此外，可以对光谱响应图进行群集，产生群集响应图，图3d中展示了三类策略：只有传出边的完全支配策略(图的左下角的单例群集)，具有传入和传出边的临时策略群集(顶部群集)，以及具有所有传入边的主导策略(右下群集)。在图3d中，只有传出边的完全支配策略(图的左下角的单个群集)、具有传入和传出边的临时策略群集(顶部群集)以及具有所有传入边的主导策略(右下群集)。最后，通过融合每个集群内的节点来收缩集群图，可以产生图3e所示的传递博弈的高级特征。

我们也可以对其他激励游戏的例子进行这种分析，比如图4a中所示的周期性游戏。注意到与早先的传递博弈例子的明显不同；在循环博弈中，响应图(图4b)中的α-Rank分布具有更高的熵(由于循环的存在，表明对许多策略的偏好，而不是一种策略)。此外，图4d中的光谱重投影显示了一组清晰的可传递节点(可视化的左侧)和一个周期诱导节点的单个簇(右侧)。收缩这张响应图揭示了这场游戏的根本周期性(图4f)。最后，基于该聚类分析，我们对原始收益表的每个策略(即，每行和每列)进行了标记。具体地说，图4a中每行(分别为列)的最左侧(分别为顶部)上的颜色编码标签对应于图14d中的群集策略颜色。这种颜色编码有助于清楚地将最终策略(即，回收表的最下面一行)识别为在游戏中执行循环关系的异常值。请注意，虽然没有单一的图形结构来总结图2中早先可视化的特定类别的随机游戏，但我们包含了以下分析。

.