MinisSelect：实用和通用的选择算法

今天，我在发布迷你选择泛型C++库方面做了很大的努力，以支持多重选择和部分排序算法。它已经在ClickHouse中使用，带来了巨大的性能优势。确切的基准和结果将在这篇文章的后面介绍，现在让我们来讲述一些关于这一切是如何发生的故事。我在Boost许可下发布了这个库，任何贡献都是非常受欢迎的。

在阅读Hacker News的大量文章、论文和帖子时，我发现每隔几个月就会有新的“闪亮”、“最快”、“通用”的排序算法从旧报纸上出现或记住，比如最近发表的关于学习排序、Kirkpatrick-Reisch排序或pdqort的论文。那就是我们基本上已经花了65年以上的时间来编写排序算法，而且我们仍然在寻找改进之处。分拣物品现在不应该是一个“解决”的问题吗？不幸的是，没有。新的硬件特性出现后，我们发现对数字进行排序实际上可以比最佳比较时间复杂度更快，我们仍然发现排序算法的改进，比如避免分区中的分支，以及像pdqsort那样试图找到好的轴心点。此外，在这一领域还有许多悬而未决的问题，比如“需要进行的最小比较次数是多少？”

排序算法方面的激烈竞争仍在继续，我相信我们还没有达到最佳排序，而习得排序看起来是下一步。但它使用的基本事实是，没有人期望在几次数组遍历中完成排序，并且我们可以在第一次数组遍历期间理解一些关于数据的内容。我们稍后会明白为什么这很重要。

我最喜欢的通用排序是pdqort，它被证明是目前最好的通用排序算法，而且它比C++提供的所有标准排序都有很大的提升。它也被用在生锈中。

大约几个月前，我开始考虑一种略微不同的排序方法--部分排序算法。这意味着您不需要对所有元素进行排序，只需找到最小的元素并对其进行排序。例如，它在SQL查询中被广泛使用，当您执行ORDER BY LIMIT N时，N通常很小，从1-10到理想的几千，更大的值仍然会出现，但很少出现。而且，天哪，与全排序算法相比，在那里做的工程和理论研究是多么的少。事实上，在小的情况下具体寻找顺序统计量的问题一直是一个未解决的问题，也没有很好的解决方案。此外，部分排序在此之后非常容易获得，您需要通过某种排序算法对第一个元素进行排序，以获得最佳比较，如果不是这样，我们将只看一个例子。是的，有很多中值算法可以推广到寻找第几个最小的元素。那么，它们是什么呢？是的，你可能知道其中的一些，但让我们复习一下，了解你的敌人是有用的。

这几乎是第一个找到第几个最小元素的算法，就像快速排序一样，但不要在两个方向递归，仅此而已。选取中间甚至随机的元素并按此元素进行划分，看看两个部分中的哪一个位于其中，更新其中一个边界，瞧，在最大的划分之后，您将找到最小的元素。好消息是，平均而言，如果我们选择随机轴心，就需要进行比较。这是因为，如果我们定义的是在元素中查找元素的预期比较次数，然后在一个阶段中，我们进行比较并统一选择任何轴心，那么即使我们在每一步中选择最大的部分。

坏消息是，最坏的情况仍然是，如果我们很不幸，总是选择最大的元素作为支点，从而进行分割。

从这个意义上说，该算法提供了许多现在使用的枢轴“策略”，例如，选取枢轴作为数组的一个元素，或者从3个随机元素中选取枢轴。或者像libcxx中的std：：nth_element一样-从中选择中间部分。

我决定将我今天要讨论的所有算法可视化，所以随机输入策略中值为3的QuickSelect如下所示：

对于像libcxx(C++llvm标准库)这样的策略，有一些很容易检测到的二次型反例，这样的模式也出现在实际数据中。反例如下：

这绝对是二次曲线。顺便说一句，这与C++标准措辞完全一致，因为它是这样写的：

长期以来，计算机科学家认为不可能在最坏的线性时间内找到中值，然而，Blum，Floyd，Pratt，Rivest，Tarjan等人提出了BFPRT算法或类似的算法，有时被称为中值算法。

将数组分成大小为5的组，并求出每组的中位数。(为简单起见，我们将忽略完整性问题。)。

当我们找到群的中位数时，至少其中至少有3/5的元素小于或等于，也就是说，2个分割的块中最大的有大小，我们有重现性。

实际上，这个常数10真的很大。例如，如果我们看得更近一点，至少是1，因为我们需要对数组进行分区，那么在少于6次比较(只能通过暴力强制)中找出5个元素中的中位数是不可能的，并且在6次比较中可以通过以下方式来完成。

如果是的话，那么问题就相当简单了。如果是，则中值为和的较小值。如果不是，则中值为和中的较小值。

所以。如果是，则解是和中较小的一个。否则，解是和中较小的一个。

所以最大值是可以的，它给了我们上界的比较，看起来它是可以达到的。还可以使用其他一些技巧来实现更低的常量，例如，对5的数组进行排序，然后比较更少的数组(例如，对5的数组进行排序，然后进行更少的比较)。在实践中，这个常量真的很大，你可以从下面的演示中看到它，它甚至被固定住了，因为它花了相当多的时间：

找到该元素的另一种方法是在一个大小数组上创建一个堆，并将其他元素推入该堆中。C++std：：Partial_Sort以这种方式工作(对第一堆进行额外的堆排序)。它对非常小的随机/上升阵列显示出很好的效果，但是随着增长开始显著下降，变得不切实际。最好的，最坏的，一般的。

由于以前的算法不是很实用，QuickSelect的平均表现也很好，1997年David Musser的“内省排序和选择算法”提出了一种名为“IntroSelect”的排序算法。

IntroSelect的工作原理是乐观地从QuickSelect开始，只有在它循环太多次而没有取得足够进展的情况下才切换到MedianOfMedians。简单地将递归限制为恒定深度是不够的，因为这会使算法切换到所有足够大的数组上。马塞尔讨论了几种简单的方法：

跟踪到目前为止已处理的子分区的大小列表。如果在任何时候，在没有将列表大小减半的情况下进行递归调用，对于一些小的正数，请切换到最坏情况线性算法。

求出到目前为止生成的所有分区的大小之和。如果超过列表大小乘以某个小的正常量，则切换到最坏情况线性算法。

这个算法进入libstdcxx，猜猜选择了哪种策略？没错，都不是。相反，他们尝试QuickSelect步骤，如果不成功，则退回到HeapSelect算法。所以，最坏的情况，平均而言

现在大多数已知的算法都结束了😈，我们可以开始研究一些特别和非凡的东西了。第一个要看的是pdqselect，它非常简单地来自pdqort，算法基本上是QuickSelect，但有一些关于如何选择适当的轴心点的有趣想法：

如果有元素，可以使用插入排序对其进行分区甚至排序。由于插入排序对于少量元素来说非常快，所以它是合理的。

如果大于，则选择-Pivot：如果少于或等于128个元素，则从以下3组中选择伪中值(或“九”，或全部相同的中值的中位数)：

如果超过128个元素，则从开始、中间、结束选择3的中位数。

使用避免分支的所选透视对数组进行分区：如果坏分区总数超过，请使用std：：nth_element或任何其他后备算法并返回。

否则，尝试通过以下方式击败分区中的某些模式(大小分别为l_SIZE和r_SIZE)：

在很长一段时间里，在寻找第th个元素方面没有实际的改进，直到2017年，C++社区非常认可Andrei Alexandresu发表了一篇关于快速确定性选择的论文，其中最坏情况中值算法变得实用，并可以在真实代码中使用。

我们现在找到了9个元素的伪中值(或9个相同中值的中位数)，这与在pdq排序中类似。在以下情况下使用该分区

介绍MedianOfMinima for。MedianOfMedians计算小组的中位数，并取其中位数来找到近似数组中值的轴心点。在这种情况下，我们追求一个向左倾斜的顺序统计量，所以我们不计算每个组的中位数，而是计算它的最小值；然后，我们通过计算这些GroupWise最小值的中位数来获得枢轴。

不是任意选择的，因为为了保持算法的线性，我们需要确保在对元素进行递归时，我们划分的元素多于元素，因此。MedianOfMaxima的实现方式与For相同。最终得到的算法如下所示。

事实证明，这是一个比上面所有算法都更好的算法(除了它不知道pdqselect)，并且显示了很好的结果。我的建议是，如果您需要确定性的最坏情况线性算法，这个算法是最好的(我们稍后将讨论几个更随机化的算法)。

所有这些算法都是好的和线性的，但它们需要进行大量的比较，比如，对所有人来说都是最低限度的比较。然而，我知道一个好的算法，它只需要比较(我也不打算证明它是最小的，但它是最小的)。让我们快速修改一下它的工作原理。

为了找到最小值，你只需将获胜者与所有其他获胜者进行线性比较，基本上第二名可能是任何输给获胜者的人，所以我们需要将它们相互比较。不幸的是，获胜者可能赢得了线性数量的其他人，我们不会得到想要的比较数量。为了缓解这种情况，我们需要举办一场淘汰赛，获胜者只玩这样的游戏：

我们下一步要做的就是把所有输家和赢家进行比较。

他们中的任何一个都可能是第二个。我们只对此进行比较。

我们能做些什么来找到第三个元素和其他元素呢？在比较计数上可能不是最优的，但至少不是那么糟糕，可以遵循这样的策略：

首先建立项目淘汰赛的二叉树。(这需要进行比较。)。最大的项目比其他项目更大，所以它不可能是第三大项目。当它出现在树的外部节点时，用保留的元素之一替换它，并找到结果中最大的元素；这至多需要比较，因为我们只需要重新计算树中的一条路径。对于保留的每个元素，总共重复此操作次数。

它将给我们提供比较的估计。假设您需要从数百万个长字符串中找到前10个，这可能是一个很好的解决方案，而不是至少比较时间。然而，它需要额外的内存来记住获胜者的路径，而我目前不知道如何删除它，因此由于分配或额外级别的间接性，使得该算法不切实际。

那时，我对选择算法的了解结束了，我决定向一个知名的人发表演讲。

在《计算机编程艺术》(The Art of Computer Programming，第三卷，Sorting and Search)一书中，我读了近100到150页，以便了解全世界对最小比较排序和选择算法的了解，发现了一个非常有趣的算法，名为弗洛伊德-里维斯特算法(Floyd-Rivest Algorithm)。实际上，就连亚历山大·雷斯库的论文也引用了这句话，但引用的方式不同寻常：

从中递归地选择两个元素：和，这样(本质上它们取和)。这两个元素将是分区的第二个轴心点，预计它们之间将包含整个列表中的第几个最小元素。

通过将数组中剩余的元素与u或v进行比较，并将它们放入适当的集合中，对数组中的其余元素进行分区。如果小于数组中元素数量的一半，则应先将剩余元素与进行比较，然后再与小于的元素进行比较。否则，其余的元素应该首先与进行比较，如果它们大于，则只与进行比较。

将该算法递归地应用于适当的集合，以选择数组中的第十个最小的。

然后在2004年证明了这种方法(在界限选择上稍作修改)至少可以与概率进行比较(并且幂中的常数是可以调节的)。

该算法试图找到合适的子样本，并证明第th个元素存在的概率很大。

然而，该算法的最坏情况仍然是，但它试图优化平均情况下的最小比较次数，而不是最坏情况下的最小比较次数。

对于小的，它真的很好，因为它只使用比较，这比所有“至少比较”的算法都要好得多，甚至对于中位数，它也是明显更好的。

因此，我决定用C++标准API对所有这些算法进行编码，并对它们进行相互测试，可能还会提交一些性能较高的东西，比如DBMS来执行ORDER BY LIMIT N子句。

我最终做了迷你精选图书馆。目前，它只是头球，但我不能保证在未来，它包含了除了锦标赛以外的几乎所有算法，这在一般情况下是很难做到的。

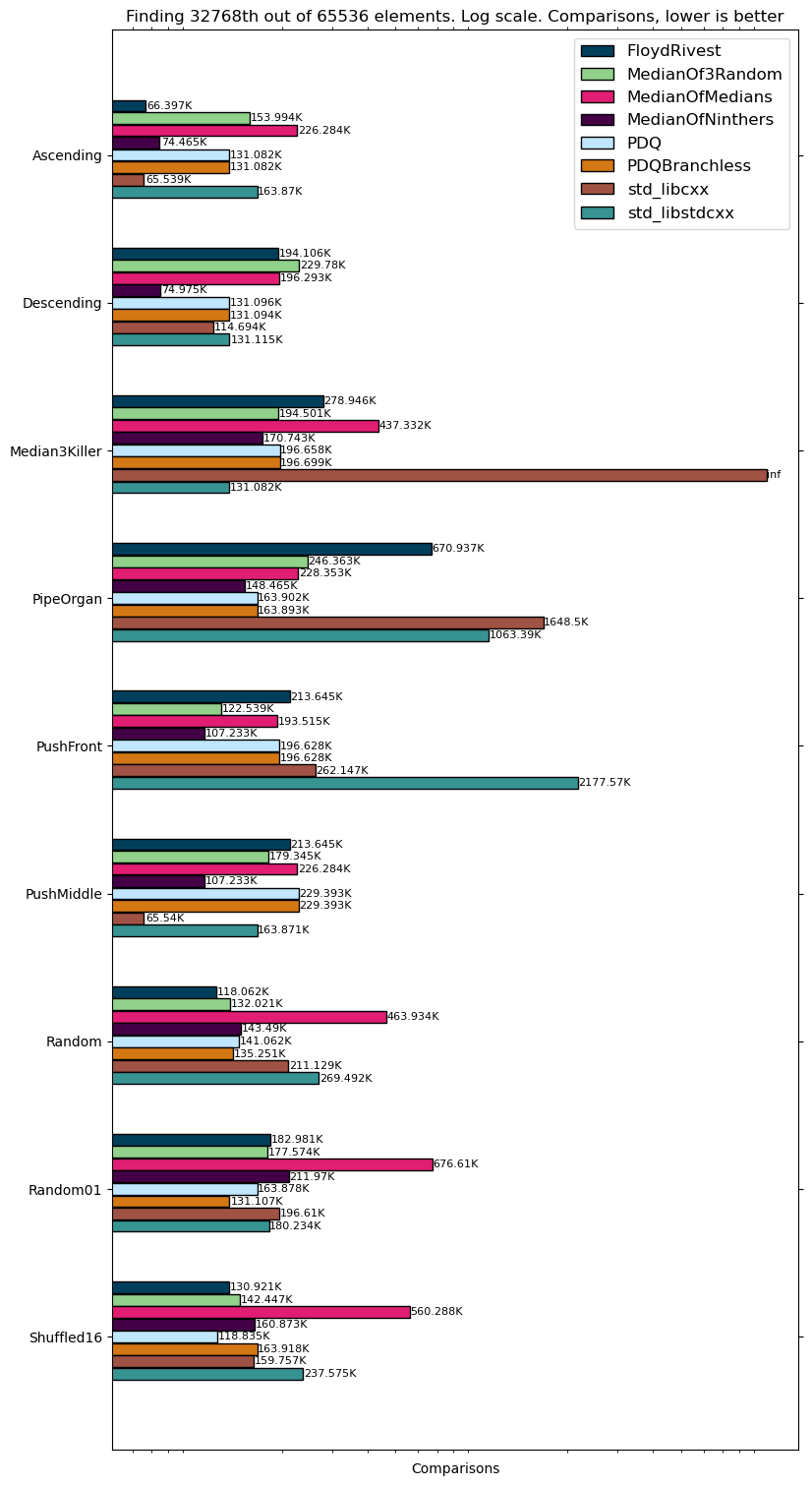
我在2.80 GHz的英特尔(R)酷睿(TM)i5-4200H CPU上进行了测试(是的，有点旧，对不起)。我们将从和数组中找出中位数和第1000个元素。基准数据：

如你所见，Floyd-Rivest在时间上优于所有其他算法，甚至在大多数情况下优于Alexandresu。一个缺点是，Floyd-Rivest在有许多相等元素的数据上表现较差，这是意料之中的，正如Kiwiel的论文中指出的那样，这可能是可以修复的。

这一努力还导致了ClickHouse的补丁，我们在该补丁中获得了以下基准：

如您所见，大多数查询都有ORDER BY LIMIT N。最顶层的查询得到了显著优化，因为STD：：PARTIAL_SORT在数据下降时工作最差，实际使用情况(如您在STRING_SORT基准测试中看到的)优化了10-15%。此外，有许多查询已经优化了5%，其中排序不是瓶颈，但仍然很不错。最终，所有查询的整体性能提升了2.5%。

其他算法的性能较差，您可以从上面的基准测试中看出这一点。因此，现在弗洛伊德-里维斯特被用于生产，而且有一个很好的理由。但是，当然，这并不会削弱亚历山德雷斯库先生的成果，在决定论和最坏的情况下，他的贡献是非常宝贵的。

我在Boost许可证下发布迷你精选，供每个人使用和调整以适应项目。上周，我花了几天时间，试图让它在所有地方都能运行(目前除了Windows，但它应该是好的)。我们支持C++11以及GCC 7+和Clang 6+。我们仔细地测试了算法的标准符合性，使用了模糊、消毒剂等。模糊成功地找到了我在最后一刻才想到的错误，所以它真的很有帮助。

如果你想使用它，请阅读API，但它应该是一个简单的sed/perl/regex替代品，没有任何问题，除了元素之间的联系可能会以不同的方式解决之外，然而，C++标准说它是可以的，你不应该依赖它。

任何我可能错过的贡献和其他算法都是非常受欢迎的，我打算将这个库作为选择算法的许多实现的参考，以便用户可以尝试为他们选择最好的选项。(我应该对排序算法做同样的事情吗？)。

这是一个很长的故事，我试图找到解决问题的办法，这些问题在过去一个月左右的时间里一直困扰着我。我可能阅读了300多页的数学/算法/讨论/论坛，以最终找到世界所知道的关于它的一切，并使其适用于具有巨大性能优势的真实世界的应用程序。我想在长期研究这个东西之后，我可以想出更好的东西，但是如果有什么事情发生，我会在这个博客里告诉你的。🙂。

具有小群体的选择算法，其中中值算法的中位数对于大小为3和4的群体在线性时间最坏情况下是有点扭曲的。

计算机编程艺术，第三卷，排序和搜索，关于最小比较排序和选择的章节

S.Battiato，D.Canone，D.Catalano和G.Cincotti提出的近似中值选择问题的一个有效算法。

今天，我将介绍用于各种选择算法https://t.co/NAJmqMOE8a.的迷你选择通用C++库。我在这方面所做的努力和研究的帖子https://t.co/YrNgZshrAJ.。其中包含了许多见解和gif！

--Danila Kutenin(@Danlark1)2020年11月11日