六角网格
2013年3月,于2015年3月,2018年4月,2019年2月,2020年5月更新。本指南将涵盖制作六角形网格的各种方法,不同方法之间的关系以及常用公式和算法。六角形网格不像正方形网格常见。我已经收集十六进制网格资源[20]已有20多年了,并主要根据Charles Fu [2]和Clark Verbrugge [3]的指南编写了导致最简单代码的最优雅方法的指南。 ]。此页面的大多数部分都是交互式的。
此页面上的代码示例以伪代码编写;它们旨在易于阅读和理解。实施指南包含C ++,Javascript,C#,Python,Java,Typescript等代码。
六边形是6面多边形。正六边形的所有边长相同。我假设我们在这里使用的所有六边形都是规则的。十六进制网格的典型方向是垂直列()和水平行()。
六角形有6个边和6个角。每边由2个六角形共享。每个角由3个六角形共享。有关中心,边和角的更多信息,请参阅我关于网格零件[4](正方形,六边形和三角形)的文章。
在正六边形中,内角为120°。有六个“楔形物”,每个楔形物的等边三角形内部为60°角。每个角都是距离中心的尺寸单位。在代码中:
函数pointy_hex_corner(center,size,i):var angle_deg = 60 * i-30°var angle_rad = PI / 180 * angle_deg return Point(center.x + size * cos(angle_rad),center.y + size * sin(angle_rad ))
要填充六边形,请在hex_corner(…,0)到hex_corner(…,5)处收集多边形顶点。要绘制六边形轮廓,请使用这些顶点,然后绘制一条线回到hex_corner(…,0)。
两个方向之间的差异是旋转,并且导致角度发生变化:角度为0°,60°,120°,180°,240°,300°,角度为30°,90°,150°,210 °,270°,330°。请注意,此页面上的图表使用的y轴指向下方(角度沿顺时针方向增加);如果y轴朝上(角度会逆时针增加),则可能需要进行一些调整。
接下来,我们要将几个六边形放在一起。在尖的方向上,六边形的宽度为w = sqrt(3)*大小,高度h = 2 *大小。 sqrt(3)来自sin(60°)。
相邻六边形中心之间的水平距离为w。相邻六边形中心之间的垂直距离为h * 3/4。
有些游戏将像素图样用于与完全不规则的多边形不匹配的六边形。我在本节中描述的角度和间距公式不会匹配六边形的大小。本文的其余部分描述了十六进制网格上的算法,即使您的六边形被拉伸或缩小了一点也可以使用,并且我在实现页面上解释了如何处理拉伸。
现在,我们将六边形组装成一个网格。使用方形网格,有一种显而易见的方法。对于六边形,有多种方法。我喜欢将立方体坐标用于算法,将轴向或双倍坐标用于存储。
最常见的方法是偏移其他所有列或行。列被命名为col(q)。行被命名为行(r)。您可以偏移奇数列或偶数列/行,因此水平和垂直六边形都有两个变体。
0,0 0,1 0,2 0,3 0,4 0,5 0,6 1,0 1,1 1,2 1,3 1,4 1,5 1,6 2,0 2,1 2, 2 2,3 2,4 2,5 2,6 3,0 3,1 3,2 3,3 3,4 3,5 3,6 4,0 4,1 4,2 4,3 4,4 4 ,5 4,6 5,0 5,1 5,2 5,3 5,4 5,5 5,6 6,0 6,1 6,2 6,3 6,4 6,5 6,6
0, 0 0, 1 0, 2 0, 3 0, 4 0, 5 0, 6 1, 0 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 2, 0 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 3, 0 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 4, 0 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 5, 0 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 6, 0 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6
0, 0 0, 1 0, 2 0, 3 0, 4 0, 5 1, 0 1, 1 1, 2 1, 3 1, 4 1, 5 2, 0 2, 1 2, 2 2, 3 2, 4 2, 5 3, 0 3, 1 3, 2 3, 3 3, 4 3, 5 4, 0 4, 1 4, 2 4, 3 4, 4 4, 5 5, 0 5, 1 5, 2 5, 3 5, 4 5, 5 6, 0 6, 1 6, 2 6, 3 6, 4 6, 5 7, 0 7, 1 7, 2 7, 3 7, 4 7, 5
0, 0 0, 1 0, 2 0, 3 0, 4 0, 5 1, 0 1, 1 1, 2 1, 3 1, 4 1, 5 2, 0 2, 1 2, 2 2, 3 2, 4 2, 5 3, 0 3, 1 3, 2 3, 3 3, 4 3, 5 4, 0 4, 1 4, 2 4, 3 4, 4 4, 5 5, 0 5, 1 5, 2 5, 3 5, 4 5, 5 6, 0 6, 1 6, 2 6, 3 6, 4 6, 5 7, 0 7, 1 7, 2 7, 3 7, 4 7, 5
Another way to look at hexagonal grids is to see that there are three primary axes, unlike the two we have for square grids. There's an elegant symmetry with these.
Let's take a cube grid and slice out a diagonal plane at x + y + z = 0. This is a weird idea but it helps us make hex grid algorithms simpler. In particular, we can reuse standard operations from cartesian coordinates: adding coordinates, subtracting coordinates, multiplying or dividing by a scalar, and distances.
Sometimes we don't have obvious algorithms for hex grids, but we do have algorithms for cube grids. Using cube coordinates allows us to adapt cube grid algorithms to work on hex grids. To use the algorithms with another coordinate system, we can convert to cube coordinates, run the algorithm, and convert back.
Study how the cube coordinates work on the hex grid. Selecting the hexes will highlight the cube coordinates corresponding to the three axes.
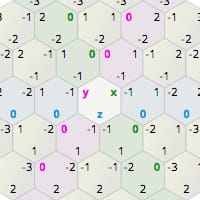
立方体网格上的每个方向都对应于十六进制网格上的一条线。尝试突出显示z在0、1、2、3处的十六进制,以查看它们之间的关系。该行标记为蓝色。对x(绿色)和y(紫色)尝试相同的操作。
十六进制网格上的每个方向都是立方体网格上两个方向的组合。例如,六边形网格上的西北位于+ y和-z之间,因此西北的每一步都涉及将y加1并将z减1。我们将在邻居部分使用此属性。
立方坐标是十六进制网格坐标系的合理选择。约束是x + y + z = 0,因此算法必须保留该值。约束还确保每个十六进制都有一个规范坐标。
有许多不同的有效立方十六进制坐标系。其中一些约束除x + y + z = 0以外。我仅显示了许多系统中的一个。您还可以使用x-y,y-z,z-x构造多维数据集坐标,并且具有自己的一组有趣的属性,在此不做介绍。
"但阿米特!"您说,我不想存储3个数字作为坐标。我不知道如何以这种方式存储地图。
通过从立方坐标系中获取三个坐标中的两个来构建轴向坐标系,有时称为“梯形”或“斜”或“斜”。由于我们有一个约束x + y + z = 0,因此存在一些冗余,并且我们不需要存储所有三个坐标。除了不显示y之外,此图与上一个图相同:
立方体坐标系有很多选择,而轴向坐标系有很多选择。我不会在本指南中显示所有组合。我已选择q作为“列” = x和r为" row" = z。这种选择是任意的,因为您可以旋转和翻转图表以将±x,±y,±z分配给q,r。
与偏移网格相比,此系统的优势在于,当您可以在十六进制坐标上使用加,减,乘和除时,算法更加简洁。该系统的缺点是存储矩形地图有点奇怪。有关处理方法,请参见地图存储部分。在我的项目中,我将轴命名为q,r,s,这样我的约束q + r + s = 0,然后当我需要第三个坐标来使算法与以下算法配合使用时,可以计算s = -q-r立方体坐标。
尽管我建议使用轴向/立方体坐标,但如果要坚持使用偏移坐标,请考虑将其加倍。它使许多算法更易于实现。代替交替,加倍的坐标使水平或垂直步长加倍。它具有约束条件(col + row)%2 ==0。在水平(尖顶十六进制)布局中,每十六进制将列增加2;在水平布局中,列增加16。在垂直(平顶十六进制)布局中,每十六进制将行增加2。这允许介于中间的十六进制中间值:
0,0 2,0 4,0 6,0 8,0 10,0 12,0 1,1 3,1 5,1 7,1 9,1 11,1 13,1 0,2 2,2 4, 2 6,2 8,2 10,2 12,2 1,3 3,3 5,3 7,3 9,3 11,3 13,3 0,4 2,4 4,4 6,4 8,4 10 ,4 12,4 1,5 3,5 5,5 7,5 9,5 11,5 13,5 0,6 2,6 4,6 6,6 8,6 10,6 12,6
0,0 0,2 0,4 0,6 0,8 0,10 1,1 1,3 1,5 1,7 1,9 1,11 2,0 2,2 2,4 2,6 2, 8 2,10 3,1 3,3 3,5 3,7 3,9 3,11 4,0 4,2 4,4 4,6 4,8 4,10 5,1 5,3 5,5 5 ,7 5,9 5,11 6,0 6,2 6,4 6,6 6,8 6,10 7,1 7,3 7,5 7,7 7,9 7,11
我没有找到有关此系统的很多信息-tri-bit.com称其为隔行扫描[5],rot.js称其为双倍宽度[6],而本文[7]则称其为矩形。其他可能的名称:砖块或棋盘格。我不确定该怎么称呼。 TamásKenéz向我发送了核心算法(邻居,距离等)。如果您有任何参考,请发送给我。
我的建议:如果您只打算使用矩形地图,而从不旋转地图,请考虑使坐标加倍或偏移,因为它们与地图的对齐方式比轴向或立方体更好。在所有其他情况下,请使用轴心作为主要系统,并仅为立方更易于使用的那些算法计算第三个立方坐标。
您可能会在项目中使用轴向坐标或偏移坐标,但是许多算法更容易以立方体坐标表示。因此,您需要能够来回转换。
轴向坐标与立方体坐标紧密相连。轴向丢弃第三坐标。多维数据集从其他两个坐标计算出第三个坐标。
函数cube_to_axial(cube):var q = cube.x var r = cube.z返回Hex(q,r)函数axis_to_cube(hex):var x = hex.q var z = hex.r var y = -xz返回多维数据集(x,y,z)
确定您使用的偏移系统类型; *-r是尖顶; *-q是平顶。每种转换都不同。
函数cube_to_oddr(cube):var col = cube.x +(cube.z-(cube.z& 1))/ 2 var row = cube.z返回OffsetCoord(col,row)函数oddr_to_cube(hex):var x = hex.col-(hex.row-(hex.row& 1))/ 2 var z = hex.row var y = -xz return Cube(x,y,z)
-1 -2 +3 -1 -1 +2 -2 0 +2 -2 +1 +1 -3 +2 +1 0 -2 +2 0 -1 +1 -1 0 +1 -1 +1 0- 2 +2 0 +1 -2 +1 +1 -1 0 xzy 0 +1 -1 -1 +2 -1 +2 -2 0 +2 -1 -1 +1 0 -1 +1 +1 -2 0 +2 -2 +3 -2 -1 +3 -1 -2 +2 0 -2 +2 +1 -3 +1 +2 -3 -2,-2 -2,-1 -2,0 -2, +1 -2,+ 2 -1,-2 -1,-1 -1、0 -1,+ 1 -1,+ 2 0,-2 0,-1 col,第0行,+ 1 0,+ 2 +1,-2 +1,-1 +1,0 +1,+1 +1,+2 +2,-2 +2,-1 +2,0 +2,+1 +2,+2
实施注意事项:我使用a& 1(按位和[8])而不是a%2(取模[9])来检测某事物是偶数(0)还是奇数(1),因为它也适用于负数。请参阅我的实施说明页面上的详细说明。
函数doubleheight_to_cube(hex):var x = hex.col var z =(hex.row-hex.col)/ 2 var y = -xz return Cube(x,y,z)function cube_to_doubleheight(cube):var col = cube .x var row = 2 * cube.z + cube.x返回DoubledCoord(col,row)函数doublewidth_to_cube(hex):var x =(hex.col-hex.row)/ 2 var z = hex.row var y = -xz返回Cube(x,y,z)函数cube_to_doublewidth(cube):var col = 2 * cube.x + cube.z var row = cube.z返回DoubledCoord(col,row)
给定一个十六进制,与之相邻的是六个六进制?如您所料,答案对于立方坐标来说是最简单的,对于轴向坐标来说还是非常简单的,而对于偏移坐标则比较棘手。我们可能还想计算6个“对角”六角形。
在十六进制坐标中移动一个空间需要将三个立方坐标之一更改为+1,而将另一个多维数据更改为-1(总和必须保持为0)。有3种可能的坐标可以改变+1,剩下的2种可以改变-1。这导致6个可能的更改。每个对应于六边形方向之一。最简单,最快的方法是在编译时预先计算置换并将其放入Cube(dx,dy,dz)表中:
var cube_directions = [Cube(+1,-1,0),Cube(+1,0,-1),Cube(0,+1,-1),Cube(-1,+1,0),Cube( -1,0,+1),Cube(0,-1,+1),] function cube_direction(direction):return cube_directions [direction] function cube_neighbor(cube,direction):return cube_add(cube,cube_direction(direction))
和以前一样,我们将使用多维数据集系统作为起点。取得Cube(dx,dy,dz)表并将其转换为Hex(dq,dr)表:
var axis_directions = [Hex(+1,0),Hex(+1,-1),Hex(0,-1),Hex(-1,0),Hex(-1,+1),Hex(0, +1),]函数hex_direction(方向):返回axis_directions [方向]函数hex_neighbor(hex,方向):var dir = hex_direction(direction)返回Hex(hex.q + dir.q,hex.r + dir.r)
使用偏移坐标时,更改取决于我们在网格中的位置。如果我们在偏移列/行上,则规则与我们在非偏移列/行上的规则不同。
如上所述,我们将建立一个需要加到col和row的数字表。但是,不能安全地添加和减去偏移坐标。相反,对于奇数和偶数列/行,结果是不同的,因此我们将需要两个单独的邻居列表。查看上面的网格图上的(1,1),看看在六个方向上的每个方向上col和row的变化。然后针对(2,2)再次执行此操作。四种偏移栅格类型中的每种表格和代码都不相同,因此请选择一种栅格类型以查看相应的代码。
var oddr_directions = [[[[+1,0],[0,-1],[-1,-1],[-1,0],[-1,+1],[0,+1]], [[+1,0],[+1,-1],[0,-1],[[-1,0],[0,+1],[+1,+1]],]函数oddr_offset_neighbor( hex,direction):var parity = hex.row& 1 var dir =奇数方向[奇偶校验] [方向]返回OffsetCoord(hex.col + dir [0],hex.row + dir [1])
选择一个网格类型:odd-r even-r odd-q even-q -1,0 -1,+1 -1,-1偶数行ALL cols 0,+1 0,-1 +1,0 -1, 0 0,+1 0,-1 ODD行ALL cols +1,+1 +1,-1 +1,0
使用以上查找表是计算邻居的最简单方法。对于那些好奇的人来说,也有可能得出这些数字。
与偏移坐标不同,加倍坐标的邻居不取决于我们在哪一列/行上。它们在每个地方都一样,例如轴向和立方体坐标。另外,与偏移坐标不同,我们可以安全地添加和减去加倍的坐标,这使它们比偏移坐标更易于使用。
var doublewidth_directions = [[+2,0],[+1,-1],[-1,-1],[-2,0],[-1,+1],[+1,+1], ]函数doublewidth_neighbor(十六进制,方向):var dir = doublewidth_directions [direction] return DoubledCoord(hex.col + dir [0],hex.row + dir [1])
选择一个网格类型:两倍宽度倍高度-2,0 -1,+1 -1,-1 0,0 +1,+1 +1,-1 +2,0
移到十六进制坐标中的“对角线”空间会将3个立方坐标之一更改为±2,将另两个立方坐标更改为∓1(总和必须保持为0)。
var cube_diagonals = [立方体(+2,-1,-1),立方体(+1,+1,-2),立方体(-1,+2,-1),立方体(-2,+1,+1 ),Cube(-1,-1,+ 2),Cube(+ 1,-2,+ 1),]函数cube_diagonal_neighbor(cube,direction):返回cube_add(cube,cube_diagonals [direction])
和以前一样,您可以通过删除三个坐标之一将其转换为轴向坐标,或者通过预先计算结果将其转换为偏移/倍数。
在立方体坐标系中,每个六边形都是3d空间中的一个立方体。相邻六边形在六边形网格中相距1,但在立方网格中相距2。这使距离变得简单。在正方形网格中,曼哈顿距离为abs(dx)+ abs(dy)。在立方体网格中,曼哈顿距离为abs(dx)+ abs(dy)+ abs(dz)。十六进制网格上的距离是以下值的一半:
函数cube_distance(a,b):return(abs(a.x-b.x)+ abs(a.y-b.y)+ abs(a.z-b.z))/ 2
一种等效的编写方式是,注意三个坐标之一必须是其他两个坐标的和,然后选择一个作为距离。您可能更喜欢上面的“二分法”形式,或此处的“最大”形式,但它们给出的结果相同:
三个坐标的最大值是距离。您还可以使用abs(dx-dy),abs(dy-dz),abs(dz-dx)的最大值来确定十六进制位于6个“楔形”中的哪个;在这里查看图表。
李向国的论文用于实际六边形图像处理的存储和寻址方案。 [10](DOI [11])给出了一个欧几里得距离的公式,该公式可以适用于轴向坐标:sqrt(dq²+dr²+ dq * dr)。
在轴系中,第三个坐标是隐式的。让我们将轴向转换为立方以计算距离:
函数hex_distance(a,b):return(abs(a.q-b.q)+ abs(a.q + a.r-b.q-b.r)+ abs(a.r-b.r))/ 2
有很多不同的方法可以在轴向坐标中写入十六进制距离,但是无论您以哪种方式编写,轴向十六进制距离都是从立方体上的Mahattan距离得出的。例如,此处描述的“差异差异” [12]是通过将aq + ar-bq-br写为aq-bq + ar-br,并使用“ max”形式而不是cube_distance的“二分”形式产生的。一旦您看到与多维数据集坐标的连接,它们都是等效的。
与轴向坐标一样,我们将偏移坐标转换为立方体坐标,然后使用立方体距离。
我们将对许多算法使用相同的模式:将十六进制转换为立方体,运行该算法的立方体版本,并将任何立方体结果转换回十六进制坐标(无论是轴向坐标还是偏移坐标)。还有更直接的距离公式;请参见rot.js手册[13],了解"奇数移位"中的公式。部分。
尽管可以将加倍的坐标转换为立方体坐标,但是从rot.js手册[14]中也可以找到距离的直接公式:
函数doublewidth_distance(a,b):var dx = abs(a.col-b.col)var dy = abs(a.row-b.row)return dy + max(0,(dx-dy)/ 2)函数doubleheight_distance(a,b):var dx = abs(a.col-b.col)var dy = abs(a.row-b.row)return dx + max(0,(dy-dx)/ 2)
我们如何绘制从一个十六进制到另一个的直线? 我用线性 ......