滥用我的计算机科学知识来欺骗Catan

我最近在Colonist.io上玩了很多《卡坦定居者》。但是，在高水平进行比赛时，您需要跟踪大量信息。人们手里拿着什么卡？哪些骰子数字没有滚动太多？甲板上还剩下哪些开发卡？您可以用一张纸手工计算所有这些，但是我很懒，很容易出错。

所以我写了一个脚本来记录我的手牌。我使用Greasemonkey脚本将每个websocket消息的副本发送到本地python服务器。服务器找到导致牌进入或离开牌手的事件，然后连续显示牌手拥有的牌。看起来像这样：

当时的通信是带有描述性名称的纯JSON，因此对涉及卡转让的所有消息进行反向工程并不难。我在计算机上玩了几场游戏，并记录了所有通信，然后分析了所有消息，以找到重要类型的ID。

尽管简单地增加或减少玩家的活动卡适用于大多数类型的交易，但有一个明显的例外：与强盗一起偷卡。在这种情况下，通过电线发送的唯一信息是卡被盗，而不是被盗。

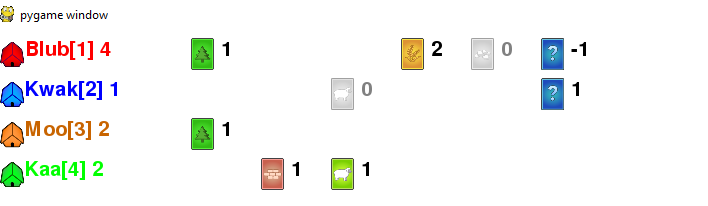
在我的初始版本中，我只有第6张卡片类型为“未知”，显示为卡片背面，并像往常一样简单地进行加减，所以它看起来像这样：

但是，这使推理变得有些困难。拥有-1张未知卡片意味着什么？如果红色然后从绿色中抽出一张牌，它将显示为0张未知牌，但这是不正确的。除非您一直注意，否则这种可能性很难在游戏中做出正确的假设。但是，脚本的整个重点是不必特别注意。

为了玩游戏，该工具需要具有准确的可操作信息。我认为更少的数据值得更可靠的保证。因此，我开发了一种新算法。偷卡的逻辑看起来像这样：

当从玩家a窃取卡时：令n为玩家a至少拥有的唯一资源的总数。对于每个资源播放器，a至少具有一个：从该资源中减去一个。添加n-1＆＃34; unknown＆＃34;将资源输入

偷牌者会像往常一样收到一种未知资源。另外，当玩家丢弃自己没有的资源时，他将丢弃未知资源，因为至少一个未知资源必须是被丢弃的资源。

这个系统运作良好，虽然我仍然很少获胜，但是我在玩游戏时可以做出更多明智的决定。我知道，如果我的第二个屏幕显示一个球员有一块小麦，那么他必须至少有一块小麦。没有更多的负面未知资源。但是，我扔掉了很多可能有用的信息，尤其是在最终游戏中，这些信息是最有价值的。

考虑这种情况：绿色有一个小麦一砖。蓝色从没有牌开始，从绿色拿出一张牌，然后丢掉小麦。在这种情况下，由于小麦被丢弃，我们可以肯定地知道绿色必须是砖。当将来的证据浮出水面时，是否有可能编写一种算法来智能地“未知”未知数。

我试图用谷歌搜索这个问题，但是找不到任何可以给我不错算法的搜索词。我必须找到自己的。

在尝试实施之前，我花了数周的时间考虑这个问题。首先，我认为我可能会为每张牌跟踪可能的位置集，然后，如果将那一组减少到一个玩家，我可以确定地分配资源，从而减少不确定性。但是，我发现在非平凡的情况下计算这些集合非常困难，并且导致了无限的可能性。假设您有一种小麦可能属于红色或绿色，而另一种小麦可能属于绿色和蓝色，那么粉红色从绿色中拿出一张卡片，现在这两张卡片也可能是粉红色的。在实践中，集合倾向于随着时间的流逝而增长而不是缩小，从不减少到足以得出结论的程度。

经过多次失败的尝试之后，我有了一个新主意。我将存储以下数据：

对于每个玩家：他们肯定拥有每种资源多少，可能拥有多少。

对于每种资源：有多少浮动成员，因为它们不属于任何参与者的“确定”组。

在这种情况下，我知道红色有木头和2个小麦，还有另外一个卡片可以是什么，也可以是矿石。从额外的浮动资源列中我们也知道，总共只有一个“丢失”小麦，它可能属于红色，蓝色或橙色。

添加资源时，我们总是可以将资源添加到定列中。减去时，如果资源存在于定列中，则可以减去它。否则，我们可以从资源的可能值中删除一个，并从浮动资源中减去一个。因此，这将不确定性降低了一个。

传输资源时，逻辑类似。只需将给予玩家的所有资源中的一个设为未知资源，而将其添加到接收玩家的未知资源中。还将每个给予玩家未知资源中的一个添加到接收玩家未知资源中。

如果资源的总空间量等于该类型的浮动资源的量，则可以肯定地知道所有这些空间都是资源。

如果玩家的空间只能容纳一种资源，那么肯定是该资源。

如果玩家最多拥有给定类型的N个资源，但总共只有M个未知资源，请将N设置为min（M，N） 如果玩家最多拥有N种给定类型的资源，但总共只有M种该类型的浮动资源，则将N设置为min（M，N） 我将更详细地解释这些。 请注意，示例并不是从初始状态实际就能到达的，在某些情况下，除了主要规则外，还可以应用其他规则。 规则1：当一个资源的空间总数可以等于该类型的浮动资源的数量时 在这种情况下，我们可以看到有两个插槽可以放置木材，而两个木材则缺少一个位置。 在这种情况下，我们将其减少为两个实木。 规则2：当仅一种类型的资源适合某个位置时，必须在该位置填充该资源 这种情况非常简单，红色缺少的资源只能是木头。 因此它必须是木头。

规则3：插槽的数量不能超过该类型的浮动资源的总数

这是在应用规则2之后我们将得到的状态。但是，现在您注意到根据我们的表格，蓝色“可能”有一块木材。但是，浮动资源中没有木材。因此，蓝色不能有任何木材。

规则4：特定资源的插槽不能超过插槽总数

在这种情况下，蓝色最多可以有2个积木，但是总共只有一张未知卡。因此，他可能只有一只砖头和一只羊。

在我可以手动执行的情况下，这些规则通常可以减少问题。但是，我设法找到了一些更罕见的减少措施。假设红色有3个未知资源，所有资源可能都是砖块或绵羊，绿色有相同的资源，但是有4个浮砖，我知道红色和绿色都有一个。我之所以能够这样做，是因为漏洞数量有限，或者资源无法放置。漏洞的定义是资源可以达到的所有位置之和之差。以及浮动的该类型变量的总数。如果漏洞数量少于给定玩家可能属于的该类型资源的数量，则该玩家必须具有该类型的max_amount-漏洞资源，因为没有足够的漏洞来放置该资源。

我相信在许多其他情况下，您可以简化图形并了解一些信息。但是，如果设置为4，则该减少似乎足以在现实世界游戏中足够快地减少未知数。在这个项目中，我学到了很多东西，包括编写用户脚本，服务器，逆向工程，以及为从未解决的问题编写算法。我鼓励每个人都去解决这个问题，或者类似的问题。

逻辑算法的代码可以在这里找到。免责声明：根本不是整洁的，而且记录不好。如果您不理解本文中的算法，则对实现的了解会更少。我还将其余的代码保密，以便从数据流中提取卡转移事件的秘密，如果其他任何人想作弊，他们至少应该努力自己对协议进行逆向工程。