超越曲线拟合的ML:因果推理和Do-微积分入门
您可能会遇到Judea Pearl的新书,以及在我的社交圈中广泛分享的相关采访。在采访中,Pearl认为我们在ML中所做的大部分工作都是曲线拟合。尽管我认为这是一个夸大的陈述(例如,通常忽略了RL),但它很好地提醒您,大多数富有成效的辩论通常是由有争议的或完全自大的评论引发的。调用机器学习炼金术就是一个很好的例子。阅读文章后,我决定再次研究他著名的do-微积分和主题因果推论。
再一次,因为这是我半周期性地发生的。我最初是在贝叶斯网络(非常不受欢迎但很高级)本科课程中学习微积分的。从那时起,我每隔2-3年在各种情况下都会遇到它,但是以某种方式它从未真正引起过共鸣。我一直以为这东西很困难和/或不切实际。最终忘记了,继续前进。直到现在,我还没有意识到这些东西的根本性。
这次,我想我已经完全理解了因果推理的重要性,因此我成为了一个全面的信徒。我知道我来晚了,但是我几乎认为这是使用数据和条件概率来理解该工具包基础知识的人们的基本卫生习惯,我为在整个职业生涯中完全忽略这一点而感到尴尬。
在这篇文章中,我将尝试解释基础知识,并说服您为什么也应该考虑这一点。如果您从事深度学习,那是理解这一点的一个更好的理由。如果将Pearl的评论解释为将深度学习与因果推理进行对比,则可能无济于事。相反,您应该将其解释为强调因果推理是深度学习的一种巨大,相对未开发的应用。不要因果关系图而灰心丧气,这些因果图看上去很像贝叶斯网络(并非偶然,因为它们都是由Pearl率先开发的),它们不与之竞争,而是对深度学习的补充。
首先,因果演算区分了人们可能想要估计的两种类型的条件分布。 tldr:在ML中,我们通常只估计其中之一,但是在某些应用中,我们实际上应该尝试或不得不估计另一个。
要进行设置,假设我们有i.i.d。从某些联合$ p(x,y,z,\ ldots)$采样的数据。假设我们拥有大量数据和最好的工具(例如深层网络)来完全估计这种联合分布或其任何属性,条件或边际分布。换句话说,假设$ p $是已知的并且易于处理。假设我们最终对变量$ y $在给定$ x $时的行为感兴趣。在较高的层次上,可以通过两种方式提出这个问题:
观察性$ p(y \ vert x)$:鉴于我观察到的变量$ X $取值$ x $,$ Y $的分布是什么。这是我们通常在有监督的机器学习中估计的。它是一个条件分布,可以根据$ p(x,y,z,\ ldots)$作为其两个边际的比率来计算。 $ p(y \ vert x)= \ frac {p(x,y)} {p(x)} $。我们都非常熟悉此对象,并且也知道如何根据数据进行估算。
介入性$ p(y \ vert do(x))$:如果我将$ X $的值设置为$ x $,则$ Y $的分布是什么。这描述了$ Y $的分布,如果我通过人为地强迫变量$ X $取值$ x $干预数据生成过程,则可以观察到这些分布,但是根据生成该变量的原始过程模拟其余的变量数据。 (请注意,数据生成过程与联合分布$ p(x,y,z,\ ldots)$不同,这是一个重要的细节)。
否。$ p(y \ vert do(x))$和$ p(y \ vert x)$通常并不相同,您可以通过几个简单的思想实验来验证这一点。假设$ Y $是我的意式咖啡机锅炉中的压力,其压力范围大约在$ 0 $和$ 1.1 $ bar之间,具体取决于开启时间。假设$ X $是内置气压计的读数。假设我们在随机时间共同观察X和Y。假设气压计正常运行,则$ p(y | x)$应该是一个以$ x $为中心的单峰分布,并且由于测量噪声而具有随机性。但是,$ p(y | do(x))$实际上不会取决于$ x $的值,并且通常与锅炉压力的边际分布$ p(y)$相同。这是因为人为地将气压计设置为某个值(例如,通过移动指针)实际上不会导致水箱中的压力升高或降低。
总而言之,$ y $和$ x $是相关的或在统计上相关的,因此看到$ x $可以预测$ y $的值,但是$ y $不是由$ x $引起的,因此设置$ x的值$不会影响$ y $的分配。因此,$ p(y \ vert x)$和$ p(y \ vert do(x))$的行为非常不同。这个简单的例子只是冰山一角。当存在大量具有复杂交互作用的变量时,干预条件和观察条件之间的差异可能会更加细微,难以描述。
根据您要解决的应用程序,您应该尝试估算这些条件之一。如果您的最终目标是诊断或预测(即观察自然发生的$ x $并推断$ y $的可能值),则需要观测条件条件$ p(y \ vert x)$。这就是我们在监督学习中已经做过的事情,这就是Judea Pearl所谓的曲线拟合。这对于一系列重要的应用程序都是有好处的,例如分类,图像分割,超分辨率,语音转录,机器翻译等等。
在最终希望根据估计的条件来控制或选择$ x $的应用程序中,应改为尝试估计$ p(y \ vert do(x))$。例如,如果$ x $是药物治疗,而$ y $是结果,则您不仅对观察自然发生的治疗$ x $和预测结果感兴趣,我们还想根据自己的意愿主动选择治疗$ x $了解它如何影响结果$ y $。在系统识别,控制和在线推荐系统中也会发生类似情况。
这也许是我以前没有掌握的主要概念。 $ p(y \ vert do(x))$实际上是一种普通的条件分布,但是它不是基于$ p(x,z,y,\ ldots)$计算的,而是基于不同的联合$ p_改为{do(X = x)}(x,z,y,\ ldots)$。 $ p_ {do(X = x)} $是数据的联合分布,如果我们实际进行了相关干预,我们将观察到。 $ p(y \ vert do(x))$是条件分布,我们将从实验者控制$ x $的随机对照试验或A / B测试中收集的数据中学到。注意,在许多情况下,实际上不可能进行干预或随机试验,或者至少不切实际或不道德。您不能进行A / B测试,以迫使您的受试者一半抽大麻,另一半抽安慰剂以了解大麻对其健康的影响。即使您不能从随机实验中直接估算$ p(y \ vert do(x))$,该对象仍然存在。因果推理和微积分的要点是:
如果我无法在随机对照试验中直接测量$ p(y \ vert do(x))$,是否可以根据在对照实验之外观察到的数据进行估算?
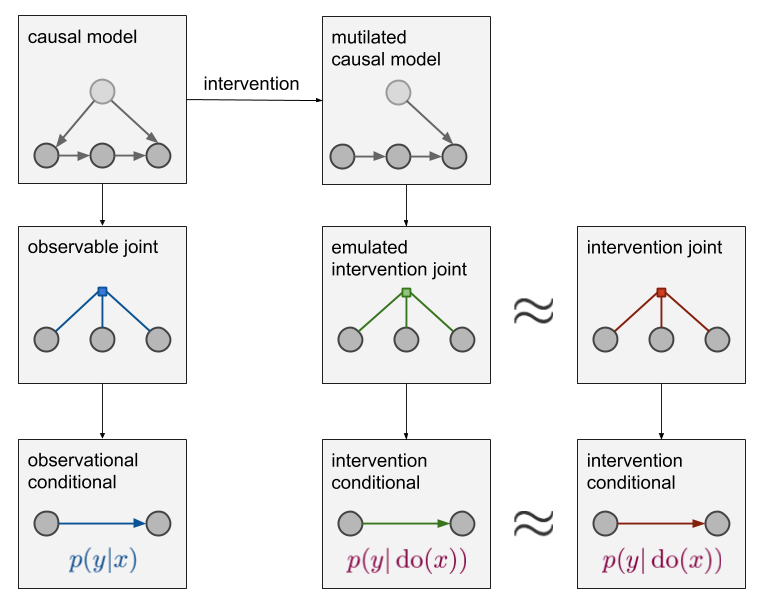
让我们从一个图表开始,该图表显示了如果我们只关心$ p(y \ vert x)$(即简单的监督学习案例)时发生的情况:
假设我们按此顺序观察3个变量$ x,z,y $。数据被内采样从3个变量的一些可观察到的关节分布中得到,由标记为“可观察到的关节”的蓝色因子图表示。如果您不知道什么是因子图,那并不重要,圆圈代表随机变量,小方块代表所连接变量的联合分布。我们有兴趣从$ x $预测$ y $,并说$ z $是我们不想推断的第三个变量,但我们也可以测量(为完整性起见,我将其包括在内)。观测条件条件$ p(y \ vert x)$是通过简单条件从该关节计算出来的。从训练数据中,我们可以建立模型$ q(y \ vert x; \ theta)$来近似此条件,例如使用使交叉熵最小的深网或其他方法。
现在,如果我们实际上对$ p(y \ vert do(x))$而不是$ p(y \ vert x)$感兴趣呢?看起来是这样的:
因此,我们仍然具有观察到的蓝色关节,并且仍从该关节中采样数据。但是,我们希望估计的对象位于右下角,即红色干预条件$ p(y \ vert do(x))$。这与介入关节有关,该关节由上方的红色因子图表示。它是与$ p $在同一域中的联合分布,但是是不同的分布。如果我们可以从这个红色分布中取样(例如,实际上进行了一项随机对照试验,我们可以选择$ x $),那么该问题将通过简单的监督学习来解决。我们可以从红色关节生成数据,然后从那里直接估算模型。但是,我们认为这是不可能的,而我们所拥有的全部是从蓝色接头采样的数据。我们必须看看我们是否能够以某种方式从蓝色关节估计红色条件$ p(y \ vert do(x))$。
如果要在蓝色和红色关节之间建立连接,则必须引入有关数据生成机制的因果结构的其他假设。我们可以预测由于交互作用而导致的分布变化的唯一方法是知道变量之间的因果关系。关于因果关系的信息不能仅在联合分布中捕获。我们必须引入比这更具表现力的东西。这是什么样子:
除了可观察的关节之外,我们现在还拥有一个世界的因果模型(左上)。该因果模型包含比关节分布更多的细节:它不仅知道压力和气压计读数是相关的,而且还知道压力导致气压计上升,而不是相反。此模型中的箭头对应于假定的因果关系方向,而没有箭头则表示变量之间没有直接因果关系。从因果图到联合分布的映射是多对一的:几个因果图与相同的联合分布兼容。因此,通常不可能仅通过观察数据来在不同的因果解释之间做出结论性的选择。
提出因果模型是一个建模步骤,在该步骤中,我们必须考虑有关世界运转方式,原因的假设。一旦有了因果图,我们就可以通过破坏因果网络来模拟干预的效果:删除$ do $运算符中所有导致结点的边。这显示在中间顶部面板上。残缺的因果模型然后产生一个由绿色因子图表示的联合分布。该关节具有相应的条件分布$ \ tilde {p}(y \ vert do(x))$,我们可以将其用作我们的$ p(y \ vert do(x))$的近似值。如果我们定性地确定了因果结构(即没有丢失的节点,并且箭头的方向都正确),则此近似值是精确的,并且$ \ tilde {p}(y \ vert do(x))= p(y \ vert do(x))$。如果我们的因果假设是错误的,则近似值可能是虚假的。
至关重要的是,为了获得这些绿色的东西,从而在观察数据和干预性分布之间建立桥梁,我们必须将数据与其他假设(如果需要的话)相结合。单凭数据并不能使我们做到这一点。
现在的问题是,当我们只有蓝色分布中的数据时,我们怎么能说绿色条件。我们处于比以前更好的状况,因为我们有了将两者联系起来的因果模型。长话短说,这就是所谓的“演算”的目的。 Do-演算使我们可以对绿色的条件分布进行按摩,直到我们可以根据蓝色分布下的各种边际,条件和期望来表达它为止。 Do-演算扩展了我们的工具包,用于处理条件概率分布,并提供了四个附加规则,我们可以将这些规则应用于带有$ do $运算符的条件分布。这些规则考虑了因果图的属性。这些详细信息无法压缩到单个博客文章中,但这是其中的介绍性文章。
理想情况下,作为do-演算推导的结果,您最终得到了$ \ tilde {p}(y \ vert do(x))$的等效公式,该公式中不再包含任何do运算符,因此您可以根据以下公式进行估算仅观察数据。在这种情况下,我们说因果查询$ \ tilde {p}(y \ vert do(x))$是可识别的。相反,如果这不可能,则无论我们尝试应用do-演算多么努力,我们都将因果查询称为不可识别的,这意味着我们将无法从所拥有的数据中估计出因果查询。下图全面总结了这种因果推理机制。
新的面板称为“可估算公式”。显示了通过推导获得的$ \ tilde {p}(y \ vert do(x))$的等效表达式,其中包括几个do-演算规则。注意,现在只需要变量$ z $来执行因果推断,如果只关心$ p(y \ vert x)$,则该变量完全不相关。如果我们不能观察$ z $,我们仍然可以进行监督学习,但是我们将无法回答因果推理查询$ p(y \ vert do(x))$。
您永远无法仅根据观察到的数据完全验证因果图的有效性和完整性。但是,因果模型的某些方面可以凭经验进行检验。特别是,因果图暗示了变量集之间的某些条件独立性或依存关系。可以凭经验测试这些依赖性或独立性,如果数据中不存在这些依赖性,则表明您的因果模型是错误的。将此想法向前推进,您可以尝试执行完整的因果发现:尝试从经验数据推断因果模型或至少是因果模型。
但最重要的是:完整的因果模型是先验知识的一种形式,您必须将其添加到分析中,以便在不实际进行干预的情况下获得因果问题的答案。仅凭数据进行推理就无法为您提供帮助。与贝叶斯分析中的先验方法不同(前者很不错并且可以提高数据效率),因果推理中的因果图是必须具备的。除少数例外,如果没有它们,您所能做的就是运行随机对照实验。
因果推理确实是基本的东西。它使我们能够回答"如果我们做了x"输入通常需要受控实验和明确干预才能回答的问题。而且我什至都没有谈到过更强大的反事实。
在某些情况下,您可以没有这种生活。通常,您实际上只是想进行正常的推断。在其他应用程序中,例如无模型RL,显式控制某些变量的功能可能使您可以回避显式回答因果问题。但是,在几种情况下以及非常重要的应用中,因果推理是唯一以有原则的方式解决问题的方法。
我想再次强调,这不是您从事深度学习还是因果推理的问题。您可以并且在很多情况下应该两者都做。因果推论和微积分使您能够理解问题并根据因果图中捕获的假设来确定需要从数据中估计的内容。但是,一旦完成此操作,您仍然需要强大的工具才能从数据中实际估算出该值。在这里,您仍然可以使用深度学习,SGD,变化范围等。这是应用于因果推理的深度学习的这一部分,而最近有关Pearl的文章则未得到充分研究。
更新:在下面的评论中,人们实际上指出了一些相关的论文(谢谢!)。如果您知道有任何工作,请在此处添加。