网类

我一直在思考Petri网。在2010年左右，我很高兴能够使用它们来描述化学反应，种群动力学以及更多来自量子物理学的思想。然后，我开始与我的学生Blake Pollard合作开发“开放式”陪替氏网，您可以将其粘合在一起以形成更大的陪替氏网。我和布莱克（Blake）专注于化学的应用，后来我和我的学生杰德·玛斯特（Jade Master）将其应用到计算机科学，并引入了一些新的数学。当Evan Patterson和Micah Halter将所有这些数学知识以及Joachim Kock的思想一起用于开发用于快速组装COVID-19模型的软件时，我感到非常高兴。

现在，我很高兴地宣布，我和Jade与Fabrizio Genovese和Mike Shulman合作，澄清了有关Petri网及其变体的许多奥​​秘：

本文充满了有趣的想法，但我只会告诉您基本框架。

它由位置（绘制为圆形）和过渡（绘制为框）组成，其定向边称为从位置到过渡以及从过渡到位置的弧。

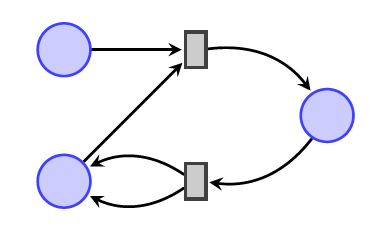
这个想法是，当您使用Petri网时，请在这些位置放置称为令牌的点，然后使用过渡将其移动：

Petri网实际上是描述单调类别的一种方式。将一堆标记放置在这些位置的方法可以得到该类别的对象，而反复移动它们的方法（如上所述）则可以得到射影。

这个想法听起来很简单。但这掩盖了一些微妙之处，研究人员至少已经奋斗了30多年。

有多种方法可以使Petri网的定义更加精确。例如：从给定的位置到给定的过渡（以及相反方向）是否存在有限的弧集，或者仅仅是自然数量的弧？如果存在有限集，那么此集是否配备了订购功能？此外，Petri网之间的形态是什么？

不同的答案对不同的目的有好处。在所谓的“个人代币哲学”中，我们在每个地方都允许有一组有限的代币。在“集体令牌哲学”中，我们只允许在每个地方使用自然数量的令牌。这就像有四个叫约翰，法布里佐，杰德和迈克的工人（您可以告诉谁做了什么）和四个匿名工人（无名无人机）之间的区别。

我们的目标是将所有内容整理清楚。我们专注于3种网络，每种网络自然会生成自己的一种单调类别：

•在严格的对称单曲面类别中，我们为每对对象选择了同构

•可交换单项类别是对称严格单项类别，其中对称同构都是恒等式，因此

因此，我们的频谱范围从铁杆个人主义（永远不会互换同一类型的两个不同事物）到铁杆集体主义，在铁杆集体主义中，同一类型的两个不同事物是如此可互换，以至于切换它们根本就无济于事！在Petri网及其变体的理论中，对两个极端的研究比对中间的研究更好。

底部有三种不同的网络类别，顶部有三种不同的单项式类别-所有这些都与伴随函子相关！由于不同类型的网络可以自由生成不同种类的单曲面类别，因此此处左侧的伴随点指向页面上方，并且在右侧向着“可交换性”的方向发展。

如果您是类别理论家，那么您将至少认识三个类别中的两个类别：

•以对称的严格单项类作为对象，严格的对称单项仿函数为它们的态射。

•以可交换单曲面类别为对象，使用严格对称单曲面仿函数为态射。可交换单曲面类别是对称严格单曲面类别，其中对称性是恒等式。

网络的类别可能不太熟悉。但是它们很简单。在这里，我将仅描述它们的对象。态射非常明显，但是请阅读我们的文章以获取详细信息。

•以子网作为对象。前置网由一组位置，一组过渡和一个函数组成，其中：

•以Σ网络作为对象。 Σ-网由一组群和离散的振动组成，其中是由一组对象生成的自由对称严格单曲面类别，没有生成态。

•以陪替氏网为对象。我们使用的术语“ Petri网”由一组集合和一个函数组成，其中是元素的多个集合

•在预网中，每个过渡都将场所的有序列表作为“输入”，并将场所的有序列表作为“输出”。我们不能置换转换的输入或输出。

•在Σ-net中，每个过渡都将位置的有序列表作为输入，并将位置的有序列表作为输出。但是，对这些列表的条目进行置换会带来新的过渡，包括新的输入列表和新的输出列表！

•在Petri网中，每个过渡都具有一组多处位置作为输入，并具有一组多处位置作为输出。多重集就像“无序列表”：条目可以重复出现，但是顺序完全没有区别。

因此，pre-net是严格的个人主义。 Petri网是严格的集体主义者。 Σ-网非常灵活，包括两种极端情况（特例）！

从前置网络中自由生成Σ-网络。如果这样做，我们将得到∑-net，以使输入和输出的排列自由地作用于过渡。 Joachim Kock最近研究了这种Σ-网络。他称它们为全粒Petri网，并视其为一类，但这也是上述函子的完整图像。

将Petri网变成Σ-网如果这样做，我们将得到∑-net，以使输入和输出的排列对过渡微不足道：排列完全不起作用。

我不会在此图中解释我们如何获得任何附加条件：

那就是有趣的分类理论的来源。我也不会告诉您有关Σ-网络的各种数学观点……也不会告诉我们。 我也不会解释我们在各种开放网络和开放类别中的工作。 我希望Mike Shulman能对我们所做的事情多说一些。 这就是为什么此博客文章的标题为“第1部分”。 但我希望您能看到重点。 有三种不同的事物，例如陪替氏网，每种事物都可以自由地生成另一种单调类别。 它们都很有趣，如果我们不将它们混淆，可以避免很多混乱！