Dyatlov Pass事件中平板雪崩释放和影响的机制

Dyatlov Pass事件是上个世纪未解决的令人迷惑的谜团。 1959年2月，九名经验丰富的俄罗斯登山者在乌拉尔北部的一次艰难探险中丧生。除其他理论外，提出了雪崩假说，但发现雪崩假说与低于正常的倾斜角度，雪崩迹象稀少，触发机制的不确定性以及受害者的异常受伤的证据不一致。解释这些观察结果所面临的挑战使我们找到了由徒步旅行者帐篷上方的斜坡上逐渐积雪吹积雪引起的平板雪崩的物理机制。在这里，我们显示了不规则地形，在坡度上进行切割以安装帐篷以及随后由强卡塔巴特风引起的积雪如何组合后，如何在适当的时间释放板坯，从而造成严重的非致命伤害，这些组合在与验尸结果一致。

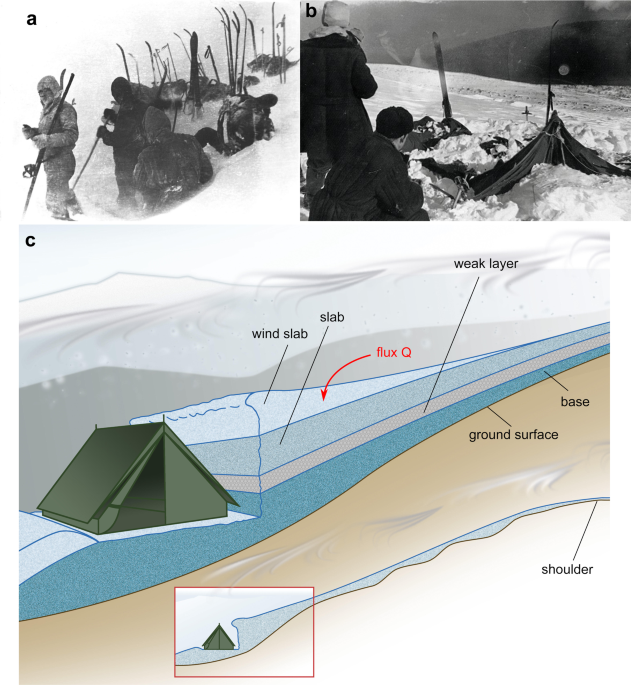
1959年2月1日夜间，在乌拉尔山脉北部的一次滑雪探险中，有9名俄罗斯徒步旅行者在无法解释的情况下死亡。该小组决定在Kholat Saykhl的山坡上建立他们的营地（图1a）;该名称在当地的曼西语中意为“死山”。午夜后发生的意外事件导致探险人员突然从帐篷内切开帐篷，并在极低的温度（-25°C以下，见下图）下，在没有适当衣服的情况下朝着超过1公里的下坡（图1b）逃到森林。补充说明3），并且在北极冷锋经过时产生强烈的方舟风1。

日落之前拍摄的Dyatlov小组的最后一张照片，同时在斜坡上进行切割以安装帐篷。图片由Dyatlov Memorial Foundation提供。 b事件发生26天后在搜索中发现的破雪覆盖的帐篷。图片由Dyatlov Memorial Foundation提供。 c在小肩部下方的斜坡上切开后，将Dyatlov帐篷的结构安装在平坦的表面上（见图2a）。帐篷上方的积雪归因于积雪的风速传输（积雪通量为Q）。

悲剧发生后的二十六天到三个月，搜查小组在森林中以及在返回帐篷的途中发现了尸体。根据1959年苏联的刑事调查，“强大的自然力量”导致Dyatlov团体死亡。但是，这支部队的性质尚未确定。谜团来自众多无法解释的观察。虽然低温被确定为主要的死亡原因，但有四名徒步旅行者的胸部或颅骨受到严重伤害，其中两人的眼睛缺失，另一人没有舌头。其中一些几乎是赤脚赤脚，在他们的一些衣服上发现了放射性的痕迹，据报道，那天晚上有漂浮在空中的橙色球体的迹象。

已经提出了几种理论来解释这一事件，包括次声引起的恐慌，动物，雪人或当地部落的袭击，四方风，雪崩，浪漫的争端，核武器试验等。最初流行的雪崩理论是由于几个相互矛盾的证据而受到质疑：1：（1）26天后到达的搜索小组未报告雪崩或碎屑的明显迹象，（2）帐篷位置上方的平均倾斜角度不足以使雪崩雪崩（低于30°），（3）在斜坡切开后至少九小时，在夜间释放假想的雪崩，并且（4）雪崩受害者的胸部和颅骨受伤并不常见。

2015年，俄罗斯联邦调查委员会（ICRF）重新开始了调查，并于2019年得出结论，雪崩是造成事故2、3的最可能原因。办公室最近对这项调查的结果提出了质疑。俄罗斯联邦总检察长的身份，他于2019年开始了自己的调查，并于2020年7月得出了与ICRF相同的结论。但是，这两项调查都没有披露上述四个抗辩的科学解释，因此一直受到亲戚，公众和研究人员的挑战。特别是，2019年的瑞典-俄罗斯远征队不同意ICRF的结论，而是提出了katabatic风对帐篷的直接影响是主要因素。

根据大量已发表的材料1、2、3、4、5、6、7、8、9，看来以前的研究缺乏重要的内容：一种可量化的物理机制，可以使雪崩假设与看似矛盾的证据相协调。识别这种机制可能会为风暴触发的积雪不稳定性的性质提供新的见解，这是这项工作的另一个重要动机。

Warning: Can only detect less than 5000 characters

下面，我们介绍了一个薄型雪板的分析模型，该雪板由在坡度上的切口上方的风雪逐渐加载而成，该模型评估了重现法医延迟估计所需的风沉积通量。随后的数值模型证实了Dyatlov组成员的观察到的损伤与失效平板动力学一致。

图3展示了所建议的可变厚度平板的延迟释放机制（基于局部地形）。在考察成员对斜坡进行切割之后（图3a），弱层的剪应力没有立即达到峰值剪切强度。由于风力驱动的积雪，斜坡在逐渐增加的长度l cw上逐渐变得受力，从而导致薄层中的剪应力增大。另外，部分雪烧结16导致风传输雪层的增强。因此，l cw的增长受到板坯厚度逐渐增加的影响，并一直持续到薄层中的剪切应力达到切口附近的峰值剪切强度τp为止（图3b）。进一步的积雪不会在弱层中调动额外的抗剪力。相反，它会在靠近切缝的地方开始软弱层的快速软化，从而导致失去平衡，基底剪切裂缝的动态上坡生长和板坯释放。

a几何形状：厚度为d的平面薄层相对于水平线倾斜角度为α。它被埋在可变深度的雪板下面，从切口处的h 0（x = 0）减小到直线上坡度（\（x \ ge l _ {\ mathrm {c}} \））的h c。切割后，高度为h w0的风雪层（在切割处）会加载斜坡，从而导致平板在h s0高度上局部增厚。 b薄层中的剪应力。

板坯释放条件是在“方法”部分中得出的，它是在无厚度，无内聚力的雪荷载下，当切口处薄弱层的切应力作用下的，具有厚度变化的内聚力平板的平面应变（2D）边值问题的解决方案。 τ0达到峰值强度τp：

$$ \ begin {array} {l} P _ {{\ mathrm {g}} 0} = \ frac {1} {2} K_0 {\，} \ rho gh_0 ^ 2 {\，} {\ mathrm {cos} } \，\ alpha，\，P _ {{\ mathrm {w}} 0} = \ rho _ {\ mathrm {w}} gh _ {{\ mathrm {w}} 0} L_0 \ cdot {\ mathrm {sin} } \ alpha，\\ \ tau _ {{\ mathrm {g}} 0} = \ rho gh_0 \，{\ mathrm {sin}} \，\ alpha，\，\ tau _ {\ mathrm {p}} = \ left（{\ rho h_0 + \ rho _ {\ mathrm {w}} h _ {{\ mathrm {w}} 0}} \ right）g \，{\ mathrm {cos}} \，\ alpha \，{ \ mathrm {tan}} \，\ varphi + c，\ end {array} $$

其中φ和c是内摩擦角和薄层的内聚力，ρ和ρw分别是原始平板和风积雪的密度，h w0是积雪的厚度在割口，K 0是静止的侧向雪压力系数，\（L_0 = l _ {\ mathrm {c}}} \ left（{1-\ sqrt {h _ {\ mathrm {c}} / h_0}} \ right ）^ {-1} \）是特征长度，其量lc，hc和h 0在图3a中定义。参数r 1和r 3由下式给出

$$ r_1 = \ frac {{1 + \ sqrt {1 + 4 \ lambda _0}}} {2}，\，r_3 = \ frac {{1 + \ sqrt {1 + 4 \ lambda _ {\ mathrm {s }}}}} {2}，\，\\ \ lambda _ {\ mathrm {s}} = \ frac {{\\ lambda _0h_0}} {{h_0 + h _ {{\ mathrm {s}} 0}}} ，\，\ lambda _0 = \ frac {{GL_0 ^ 2}} {{E ^ \ prime h_0d}}，$$

其中hs0和d的量在图3a中定义，G是薄弱层的剪切模量，E'是板坯的平面应变弹性模量。数值λ0和λs分别表征了积雪运输前后的薄弱层系统的几何量L 0与特征弹性长度14之间的比率。

图4a，b提供了计算雪崩释放时间的概念框架。已经证明（参见方法）只有在薄弱层φ的内摩擦角落在以下范围内时才可能延迟释放板坯（图4a）：

$$ \ begin {array} {l} {\ mathrm {tan}} \，\ varphi _ {{\ mathrm {min}}} {\，}＆lt; {\，} {\ mathrm {tan}} \\， \ varphi {\，}＆lt; {\，} {\ mathrm {tan}} \\\\ varphi _ {{\ mathrm {max}}}} \ left（{\ lambda _0} \ right），\\ {\ mathrm {tan}} \，\ varphi _ {{\ mathrm {min}}} = {\ mathrm {tan}} \，\ alpha-\ frac {c} {{\ rho gh_0}} \ sqrt {1 + {\ mathrm {tan}} ^ 2 \ alpha} + r_1 \ frac {{K_0h_0}} {{2L_0}}，\\ {\ mathrm {tan}} \，\ varphi _ {{\ mathrm {max}}} \ left （{\ lambda _0} \ right）= \ frac {{1 + \ sqrt {1 + 4 \ lambda _0}}} {{5 + \ sqrt {1 + 4 \ lambda _0}}} {\ mathrm {tan} } \，\ alpha，\ end {array} $$

a延迟释放平板的条件。 b对于风荷载的临界高度的界限。 c预测延迟与法医估计延迟。

对于上述范围内的φ值，当h w0达到最小\（（h _ {{\ mathrm {w}} 0，\，{\ mathrm {min}}}）\）时，会出现最短和最长的延迟。和最大（（h _ {{\ mathrm {w}} 0，\，{\ mathrm {max}}}）\）临界值分别由无限烧结速率和零烧结速率定义（图4b）：

$$ \ begin {array} {l} h _ {{\ mathrm {w}}}，\，{\ mathrm {min}}} = h_0 \ frac {\ rho} {{\ rho _ {\ mathrm {w} }}} \ frac {{{\ mathrm {tan}} \，\ varphi-{\ mathrm {tan}} \，\ varphi _ {{\ mathrm {min}}}}}}} {{{\ mathrm {tan} } \，\ varphi _ {{\\ mathrm {max}}} \ left（{\ lambda _0} \ right）-{\ mathrm {tan}} \，\ varphi}}，\\ h _ {{\ mathrm {w }} 0，\，{\ mathrm {max}}} = h_0 \ frac {\ rho} {{\ rho _ {\ mathrm {w}}}}} \ frac {{{\ mathrm {tan}}} \，\ varphi-{\ mathrm {tan}} \，\ varphi _ {{\ mathrm {min}}}}}} {{{\ mathrm {tan}} \\，\ varphi _ {{\ mathrm {max}}} \\ left （{\ lambda _ {\ mathrm {s}}} \ right）-{\ mathrm {tan}} \，\ varphi}}。\ end {array} $$

最后，通过将\（h _ {{\ mathrm {w}} 0} \的界限代入方程中，我们获得了延迟释放时间的界限（图4c）

提议的分析框架允许根据法证数据从9.5到13.5 h的可能延迟范围内反算风沙通量Q（请参阅补充说明1）。对于Dyatlov案例的几何和物理参数（在方法中提出并在补充说明6中进行了讨论），观察到的延迟范围（图4c）的合理拟合为\（Q = 0.008 \，{\ mathrm { kg}} \，{\ mathrm {m}} ^ {-1} {\ mathrm {s}} ^ {-1} \）。关于积雪的广泛研究表明15，这种沉积通量要求平均风速在2-12 2m·s -1范围内，这与事故当晚来自附近气象站的数据相符（见补充说明3）。

除了解释延迟之外，我们提出的机制还提供了故障前平板的几何形状，这可以帮助您了解相对较小的平板如何导致严重但非致命的伤害。我们通过将新颖的数值模型与现有数据相结合来解决这个问题，这些数据是由汽车行业17、18进行的冲击试验得出的人胸伤害。

基于材料点法（MPM）和有限应变弹塑性19的三维数值模拟（请参见方法）表明，这种小板雪崩影响了躺在帐篷地板上的徒步旅行者并充满了挖掘的空间，但没有明显的影响。跳动，与据报道缺乏明显的雪崩征兆一致（图5）。板坯拉伸破坏的预计长度为5.0μm，与分析模型一致。模拟的雪板在撞击时达到约2μm/ s的速度（见图SF 7，补充说明5和补充电影1、2）。在这种速度下，体积为0.125–0.5 m 3且密度为400 kg / m 3的典型积雪对人胸的影响导致胸廓最大变形在28％至34％之间，对应于Kroell等人通过碰撞测试报告的数值。以10 kg的质量以7 m / s的速度撞击胸腔时为18（图5，补充说明5和补充电影3-6）。根据18级缩写伤害量表（AIS），与Dyatlov事件的犯罪调查的尸检报告相一致，这些偏斜将主要导致中度至重度非致命性胸腔受伤。在雪崩受害者中通常不会观察到此类伤害，因为撞击很少发生在坚硬的障碍物上。在Dyatlov案中，受害者被困在下落的平板和帐篷地板之间，帐篷地板被放置在由雪橇1加固的压实雪上。

蓝雪颗粒表示满足产量条件的区域。插图显示了碰撞试验的模拟（3D MPM）胸部挠度（通过原始胸部高度20µcm标准化），碰撞试验中有10µkg的刚性质量以7µm / s的速度撞击胸部（黑色曲线），并且受到了密度为400 kg / m 3的0.125、0.25和0.5 m 3弹塑性积雪，速度为2 m / s（分别是橙色的点划线，红色的虚线和红色的实心曲线）。伤害级别对应于AIS 11。

在过去的20、19、20、21、22、23年中，雪和雪崩研究取得了重大进展，这使得人们可以更好地了解雪崩动力学以及与雪板雪崩释放有关的过程24、25、26、27、28。 ，在文献中还没有发现与Dyatlov谜启发的机制相似的机制，并且其物理定量需要新的理论发展。

在我们的分析模型中，这些进展包括厚度随空间变化的积雪板，以及由于风雪的烧结而引起的演化，从而影响了

......