遍历：最被忽视的假设（neurabites.com）

掷硬币–您正面赢了50％的净资产，但在尾方仅损失40％的净资产。尽管看起来不错，但最终您还是有可能破产。

遍历性是集合平均数等于时间平均数的时间。例如，当10个人做某件事一次时产生的结果与1个人做10次同样的结果。

对于非遍历系统，总体性能是单个性能的误导性指标。总体而言，尽管大多数人都输了，但平均水平看起来还是不错。

尽管大多数金融系统都是非遍历的，但经典经济理论的基础还是基于谬误的遍历的假设-从DCF估值到我们衡量GDP增长的方式。

将这些遍历性概念付诸实践，现在我增加了对不可恢复风险的权重。

在查看平均值时应该查看中位数。例如用于个人收入分配

查看集合，而不是更精细的细分。例如今年的销售额增长了10％，但全部来自新的业务线，而核心业务保持平稳

就像《黑天鹅》，抗脆弱性，非线性和可选择性一样，这是纳西姆·塔莱布（Nassim Taleb）发出声音的另一个概念。但是，这一点比其他人受到的关注要少得多。

尽管赔率不错，但还是要破产：一个赌博示例，遍历与非遍历，以及凯利准则

人体工程学经济学：现代资产组合理论，DCF模型和GDP中人体工程学假设的普遍性和危险性

遍历假设是平衡统计力学的关键分析工具。它基于这样的假设，即可观测时间的平均时间和期望值相同。在有效的地方，动态描述通常可以用更简单的概率描述代替-从模型中基本上省去了时间。

一口吧？现在让我们在这里放置定义，并通过更容易理解的示例迈出第一步。

抛硬币。如果是正面的话，您的净财富将增加50％。如果拖尾，则您的净财富减少了40％。

乍一看，这款游戏似乎很受您的青睐。从长远来看，我们期望正面和反面的数目相等。鉴于您从每个头得到的报酬要多于在每个尾部所受到的惩罚，因此您应该尽可能多地玩游戏，对吗？此外，即使您最终连败，也永远不会输光所有金钱，只输掉40％的钱。您可以赢回丰厚的回报。对？

好吧，这是一个模拟，如果您玩了50次，会发生什么。 这里似乎没有趋势。 考虑到有利的赔率，我们期望上升的趋势。 但是我们最终无所适从。 奇怪。 也许这家伙倒霉？ 看起来他们停留在零。 令人惊讶地给出了有利的赔率。 我们希望数学能够抵消倒霉的前50轮比赛。 这家伙真的很倒霉吗？ 请记住，他们永远不会破产，因为损失是他们目前财富的40％。 现在，下降趋势相当明显。 现在，让我们为100个人同时进行50轮比赛进行模拟，并在一幅图像中显示每个时间点的平均结果（财富）。 绿线显示每个x值（时间）有100个玩家的平均y值（财富）。 同样，没有明确的趋势。 模拟10,000个玩家（红线），我们开始看到趋势。 平均而言，这组10,000名玩家的利润约为10倍。

玩此游戏时，一百万人的平均财富呈指数增长。 （从3月的所有COVID-19图形中回想起，对数轴线性增长意味着指数增长。这是区分指数增长与仅非常快速增长的巧妙技巧。） 一个更技术性的答案：遍历。 或更具体地说，对于这个非遍历游戏来说，是对遍历性的错误假设。 让我们更深入地研究，并探讨一些针对100美元起价的个人情况。 同样，我们借助Excel中的二项式概率分布将这种逻辑重复进行更多轮。 H 5次，T 5次（在这里顺序无关紧要）：$ 100 x 1.5 5 x 0.6 5 = $ 59 H 50次，T 50次（在这里顺序无关紧要）：$ 100 x 1.5 50 x 0.6 5 = $ 0.5 （i）总的来说，支出对玩家是有利的，因为平均财富始终高于100美元的起始值。 这是整体平均值。

（ii）但是这种不对称的收益仅在合奏方面有利（将合计除以玩家人数）。收益结构在时间（时间）维度上不利于个人。在个人层面上，人们玩的时间越长，他们失去的可能性就越大。赌徒的废墟。因此，看整体收益是单个收益的不良指标。

因此，随着游戏的进行：房屋赔钱的原因是他们付出的钱超过了收到的钱，而更多的人成为了失败者，只有少数幸运的人变得富裕起来。 （在上下文中，连续100次获得的收益，$ 4.1 x 10 19使全球GDP达到$ 100t，并乘以40万年。因此，我们今天创造的所有财富乘以比智人的生存时间还长的时间。 2 100中有1的可能性甚至更高。）

我们探索的示例有多种变体：例如三重或全无硬币翻转。我们得到了相似的结果，只是人们没有破产，而是完全破产，并在那里结束了比赛，而有些幸运的人则疯狂地富起来。

显然，模拟一个人玩10,000回合与模拟10,000个人玩一回合产生了截然不同的结果。

一个人长时间的轨迹（时间平均值）会在一个瞬间（整体平均值，也就是空间平均值）为许多个人轨迹的总和提供不同的结果。 （注意：我们可以用期望值/结果/概率/收益来代替此语句中的“平均”。）

造成这种差异的原因是时间的路径依赖性。整体维度和时间维度之间的这种区别至关重要。

在我们操纵的掷硬币游戏中，大多数玩家会遭受连败的局面。但是，尽管大多数人都是失败者，但还是出现了一些非常幸运的人，并将整体平均水平提高了。该游戏是非遍历过程/结果/游戏/系统的典型情况。

常见的错误是假定遍历。将合奏和时间平均值混为一谈。假设非遍历系统是遍历的（类似于将非线性系统误认为是线性的）。

（i）布朗运动是由粒子彼此和/或与容器壁的碰撞引起的随机运动。对于布朗运动的气体分子，在容器中每个区域所花费的平均时间与该区域的体积成正比。也就是说，在很长的时间范围内，给定分子在容器一半中所花费的时间等于在另一半中所花费的时间。

（ii）假设的例子。考虑美国人口的财富状况/社会阶层。如果个人财富状况完全符合人体工程学，并假设我们永远生活，那么我们将根据代表性样本中每种财富状况的发生频率，花费一生的相同比例。因此，在一个给定的世纪中，蓝领阶层大约20年，中下阶层大约60年，中上阶层10年，上阶层9年，百分之一表示1年。稍后将在此示例中提供更多信息。

（iii）颜色感知。我们的大脑每20毫秒进行一次视觉测量。因此，如果我们以更快的速度切换颜色，大脑将只感知到时间平均值，该时间平均值会与物理上混合的两种颜色的总体平均值收敛。资料来源：遍历，监狱和时间尺度；遍历经济学

（i）神话般的人月。 “如果需要2个工程FTE在1个月内（即2个工时）完成项目，那么让我们聘请8名工程师并在1周内完成。”

（ii）“如果1名孕妇需要9个月才能分娩，那么9名孕妇应该只需要1个月。”

（iii）“食谱说在200度下烘烤60分钟，但我只是在400度下烘烤30分钟。”

根据遍历的学科渊源，您会找到其他定义。但是它们都收敛到相似的中心点。

数学：遍历性是（离散或连续）动力系统的一种属性，从量度理论的角度来看，它表示系统的不可约形式。

计量经济学：如果可以从过程的单个足够长的随机样本中推断出其统计属性，则该过程是遍历遍历的。

在某些情况下，您可能可以访问大量样本，但时间不够。在另一些情况下，您可能只能获得少量样本，但是您有很长一段时间的数据。只要您的测量是遍历的，您就可以方便地推断出

物理学：遍历假设说，在很长一段时间内，系统在具有相同能量的微状态相空间的某个区域中所花费的时间与该区域的体积成正比，即所有可访问的微状态都是可装备的在很长一段时间内。

同样，这是链接时间和空间（合奏）–如果是遍历的，则可以将其中的数据转换为另一数据。

通用字典。遍历：属于或关于过程的，其中每个序列或相当大的样本均代表整个过程（就统计参数而言）

回到布朗运动示例。我们之前看到的是完全弹性的墙（反弹时没有能量损失）。但是，想象一下墙壁是否完全是塑料的（接触时吸收所有能量）。也就是说，粘性。分子将在第一次接触时粘附，并且其在盒子给定区域中的时间将不再与该区域的体积成比例。这样的系统将是严格非遍历的。高不可逆性。 （有遍历，弱于非遍历和强于非遍历的内容。在这里不再详细介绍，但是如果您想了解更多技术，请查看此视频。）

回到假设的财富例子。实际上，当有人输入1％时，他们很有可能会保持在1％中。而且，如果某人出生在最低的20％，那么他们很可能会留在那里。社会流动性已经走了很长一段路，但是还有很长的路要走。

“动态平等是恢复遍历，使时间和整体概率可替代的要素。” –游戏中的皮肤（2018年），纳西姆·塔莱布

以我们之前看到的操纵过的投币游戏为例，但是您不必在每个回合中调整您的下注大小，而不必被迫下注您的全部净资产。我们看到每次都全押是一个愚蠢的想法–您最终将衰减为零。但是，鉴于整体上的有利赔率，那么最好就走开吗？

实际上存在一个数学上证明的最佳赌注大小，具体取决于赔率（或赔付）的有利程度。这是凯利准则。 （请注意，此处的收益和赔率可以互换。“普通硬币的正面收益为1.50美元，尾部的收益为0.60美元”与“正面硬币的收益为1.00美元，偏头硬币的收益为1.00美元”相同） ）

下注太小，您会错过利用有利的下注的机会。下注太大，最终您会破产。凯利投注恰到好处。公式的版本多种多样，我发现这是最简单的：

a =您可能会损失的部分（即，如果损失，则从1减至1 – a）

b =您可以赢的分数（即，如果赢，则从1增至1 + b）

因此，在我们操纵的投币游戏中，最佳下注大小为= 0.5 / 0.4 – 0.5 / 0.5 = 0.75。不管我们有多少钱，我们都应该投入75％的钱。 （从公式中我们可以看出f *可能为负，在这种情况下，最佳策略是将赌注押在另一边。）

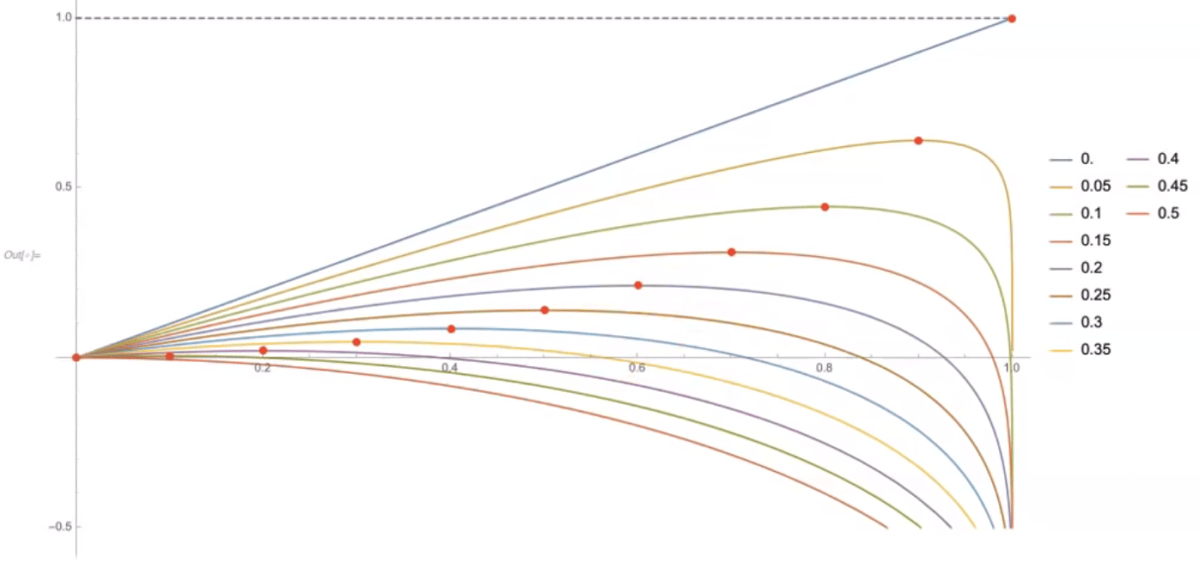
彩色曲线显示了给定赔率下给定赌注大小的预期长期收益。每条彩色曲线代表不同的几率。从顶部开始，蓝线0的赔率是0％。从底部开始，红色曲线有50％的机会丢失。

红点是凯利（Kelly）的赌注，长期而言，它能在给定的赔率下获得最大的回报。

显然，如果您的赔率是0％，则最佳下注金额是100％。如果不能输的话，全押。偏见越有利，您应该越积极。相反，如果您的输赢赔率大于50％，则最佳下注额为筹码的0％。为什么在不利的游戏中下注？

请注意，即使您输的几率只有5％，但如果赌得太久，也会陷入无法挽回的输球。这显示在图表上红点的右侧。

首先是要了解关于未来的所有参数，并进行优化的投资组合构建，除非有人对未来有如神似的了解，否则这是一种谬论。 ……人们需要了解整个未来所有资产的整体联合概率分布，以及未来所有时间财富的确切效用函数。而且没有错误！ [第二]，凯利的方法……不需要联合分配或效用函数。它非常强大。 …估计预期利润与最坏情况的回报之比，并进行动态调整以避免破产。 …最坏的情况是有保证的（将您的钱中的80％留在储备中）…因此，假设某人有优势（作为唯一的中央信息），则采取动态的可变博彩策略，在亏损之后变得更加保守（ “减少损失”）和“用房子的钱”更具侵略性。第一种策略仅被学术金融经济学家所接受-游戏中没有皮肤的空衣服-因为您可以使学术界的人们用方法1比用方法2更好地写BS论文。另一方面，每个生存的投机者都明确或隐含地使用方法2（证据：Ray Dalio，Paul Tudor Jones，Renaissance，甚至是Goldman Sachs！）对于第一种方法，请考虑LTCM和银行业失败。

尽管大多数金融系统都是非遍历的，但经典经济理论的基础还是基于谬误的遍历假设。均衡不是经济的自然状态。许多模型通过将等式简化为整体等效项来消除它们的时间。这在大多数汇总度量和风险管理方法中导致对安全性和乐观的错误认识。数量路径在时间上的重要性被低估了。

但是，该理论基于遍历假说，将整体总收益与个人随时间变化的路径收益相混淆。

现代投资组合理论利用整体收益或平均收益来计算投资组合的预期收益。但是，单个投资组合经理对整体收益不感兴趣，而对单个投资组合随时间的收益（即与路径相关的收益）不感兴趣。收获是合奏和时间平均收益率不相等，因为收益率分布不正常。这称为非遍历。 – NZS Capital的《复杂性投资白皮书》

DCF（折现现金流量）模型是用于评估公司价值的教科书方法。基本上，它涉及对所有未来现金流量进行汇总，同时对从现在起远小于今天的未来美元进行估值。该模型具有遍历性，因为它通过将时间维度转换为整体期望值（净现值）来减少时间维度。尽管在某些情况下（与所有模型一样）有用，但我们需要充分了解其假设和局限性。

首先，所应用的折扣系数会随着时间的推移而保持不变-这种假设并不十分成立。其次，这种固定的折现率通常来自加权平均资本成本（WACC），而加权平均资本成本又是基于股权风险溢价和beta的有争议概念，两者都很容易操纵。

股票风险溢价是除beta之外的额外风险，即除一般市场风险之外的其他风险

DCF模型中的所有这些概念均来自资本资产定价模型，其源自期望效用理论，该期望效用理论源自1738年的Bernoulli论文，该论文有一个最近才指出的关键数学错误（由Ole Peters指出）。这是TED的演讲。

GDP（国内生产总值）：在二战后和二战后的生产时代中普及的一种衡量标准，用于对经济活动进行定量掌握，并作为衡量国家繁荣的替代指标。大多数批评集中在它所排除的内容上：环境的可持续性，强调贸易顺差的重要性，诸如幸福之类的社会/文化/情感因素，以及其他充分合理的公式缺陷选择。同时，很少有人讨论承认GDP是一个整体值。它假设遍历。

请记住，要使某项遍历遍历，合计所发生的事情（总体平均）必须与个体随时间所发生的事情（时间平均）相同。当我们说GDP增长2.3％，人们为之鼓掌时，是指总计增长2.3％。正如我们在经过操纵的掷硬币游戏中的非遍历分布中所看到的那样，对于大多数人来说，这种平均结果远非具有代表性的结果。 GDP的增长是个人财富增长的不良指标。因为一些真正有钱的人拉高了平均水平。

奥莱·彼得斯（Ole Peters）撰写了有关民主的国内产品（DDP）的文章。在一个假设的国家/地区，有100个的年收入为5万美元。假设在明年，一个人奴役了所有人，并偷走了他们的全部收入（500万美元= 5万美元x 100）。即使现在大多数人的生活状况恶化，GDP也将保持不变。如果这个人以某种方式将其收入从500万美元增加到550万美元，那么该国的增长率将达到10％。本质上，在这种富裕制度下，国内生产总值由美元而不是个人加权。

另外，如果我们不将总增长计算为美元加权平均增长（合计），而是将每个个体的时间平均计算为该怎么办？也就是说，我们采用每个人的收入增长率，然后取这些平均值的平均值。 DDP给予个人同等的权重，而不是美元。在这种情况下，DDP的增长将显示为一个巨大的脂肪负数，因为大多数人看到了减少。

我们的生活是非遍历的。它取决于时间。简而言之，我们只活一次。

对于个人而言，不可挽回的风险包括死亡，永久性残疾，严重的精神疾病，不可挽回的个人品牌损害（犯下严重罪行）等。

因此，我采取了非常标准的措施来最小化这些可能性：在旅途中要格外小心，不要打架等。

然后，有一些不那么明显但普遍得多的事情会慢慢杀死您：压力过大，睡眠质量差，营养不良等。（注意：心血管疾病是导致死亡的主要原因。每天睡眠少于6个小时会增加患心血管疾病的风险20％。帕累托优化健康结果：专注于20％的行动（转化为80％的结果）（对于身心健康而言）。

就个人而言，我知道自己在旅行中将面临更大的风险。我对目的地不足的迷恋使我到达了诸如蒙古，俄罗斯的西伯利亚部分，缅甸，乌兹别克斯坦，吉尔吉斯斯坦，埃塞俄比亚和乌干达的地方。

在这样的旅行中，我遇到了各种各样的麻烦。在激流泛舟时遇到鳄鱼，面对一个小睡，他在我睡着时闯入房间，用冻僵的手指在冬天的山路上驾驶摩托车，在激烈的部落冲突中滞留在沙漠中几个小时，全力骑着马速度无

......