梯度下降模型是内核机器

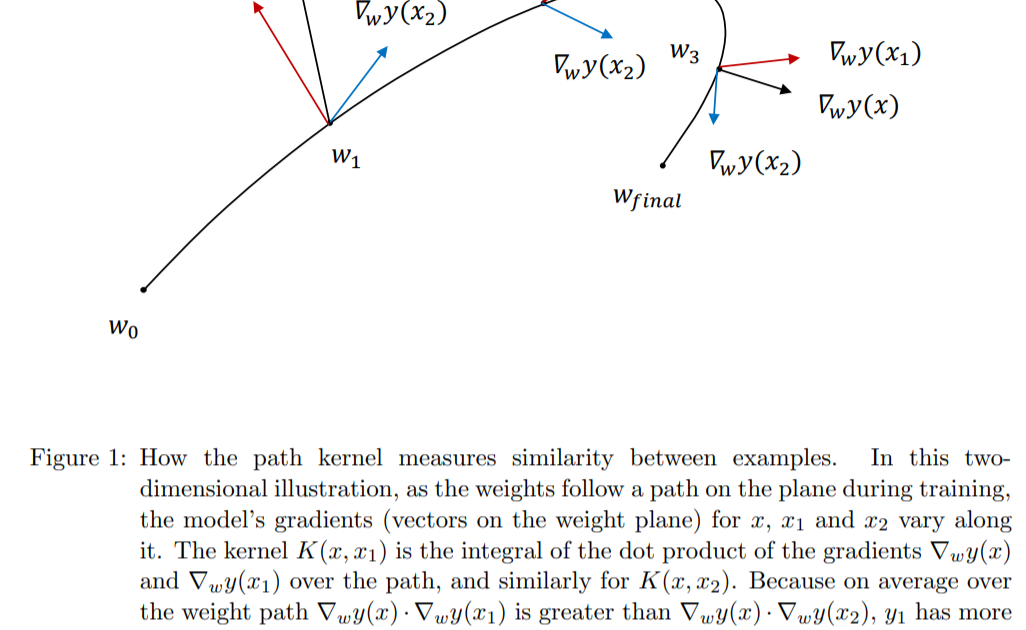
本文表明，由梯度下降训练（例如深层神经网络）产生的模型可以表示为相似度函数（内核）的加权总和，这些函数可度量给定实例与训练中所用示例的相似度。内核由参数空间中模型梯度的内积定义，并在下降（学习）路径上进行积分。粗略地说，两个数据点x和x＆＃39;相似，即如果它们对梯度下降中的模型参数具有相似的影响，则具有较大的核函数K（x，x＆＃39;）。关于学习算法，x和x＆＃39;。具有相似的信息内容。学习的模型y = f（x）将x与相似的数据点x_i匹配：结果值y只是内核值K（x，x_i）的加权（线性）和。

该结果非常清楚，如果没有由生成实际数据的地面真理机制（例如某个自然过程）强加规律性，则神经网络不太可能在与（由内核定义）强烈偏离的示例上表现良好所有培训示例。鉴于基本事实模型的复杂性（例如维数），可以对成功训练所需的数据量进行限制。

该公式将深度学习模型的非线性定位在内核函数中。只要损失函数与训练数据相加，核的叠加就完全是线性的。深度学习的成功通常归因于其自动发现数据新表示的能力，而不是像其他学习方法那样依赖手工功能。但是，我们表明，通过标准梯度下降算法学习的深度网络实际上在数学上近似于内核机器，这是一种简单地存储数据并直接通过相似性函数（内核）将其用于预测的学习方法。通过阐明深层网络权重实际上是训练示例的叠加，可以大大增强深层网络权重的可解释性。网络体系结构将目标功能的知识整合到内核中。这种更好的理解应该导致更好的学习算法。

从论文中：...在这里，我们显示了通过这种方法学习的每个模型，无论使用哪种体系结构，都大致等效于具有特定内核类型的内核计算机。该内核在学习过程中在模型参数所采用的路径附近的两个数据点处测量模型的相似性。内核机器存储训练数据点的子集，并使用内核将它们与查询匹配。因此，深层网络权重可以看作是内核特征空间中训练数据点的叠加，从而可以有效地存储和匹配它们。这与深度学习作为一种从数据中发现表示的方法的标准观点相反。 ...

……深层网络的权重可以直接解释为训练样本在梯度空间中的叠加，其中每个样本都由模型的相应梯度表示。图2对此进行了说明。研究深度网络输出的一种经过深入研究的方法涉及在欧几里得或其他简单空间中寻找与查询接近的训练实例（Ribeiro et al。，2016）。路径核告诉我们进行这些比较的确切空间是多少，以及它与模型的预测如何相关。 ...

另请参见讨论该论文的视频。