如何使用图论解决秘密圣诞老人问题

每年我们的家人都会举办一次秘密圣诞老人活动。我们没有给每个家庭成员廉价的礼物，而是随机分配接收者，这样每个人都会从一个匿名的圣诞老人那里得到一份好礼物。

我们决定建立一个简单的网站，每个家庭成员都可以在活动开始时注册，填写愿望清单并获得收件人的姓名。有许多网站和应用程序可用于此目的，但我们决定拥有自己的服务，以对排序算法进行一些修改。

每个参与者注册后，我们需要运行排序算法来确定谁向谁赠送礼物。为了解决“秘密圣诞老人”问题，我们需要找到这种排序算法。

我们有所有参与者。让我们随机抽取第一个。假设我们有鲍勃。接下来，我们从初始数组中删除Bob并从中获得随机参与者。假设我们得到了爱丽丝。因此，鲍勃给了爱丽丝礼物。然后从阵列中删除Alice，并得到一个随机参与者，该参与者将成为Alice的接收者。等等。重复直到初始数组为空。最后一位参加者是第一位Bob的Secret Santa。圣诞老人链已完成。

这种算法称为朴素。每个步骤都是显而易见的，它模仿了从帽子或彩票机中获取代币的人们。在大多数情况下，朴素算法不是最佳算法，并且性能不高，但是此任务非常容易，因此朴素算法是最佳算法，具有O（n）性能和O（1）内存。

下一步是修改问题，并对我们的算法增加一些其他要求。这就是为什么我们想要创建自己的服务。有时，由于纯粹的随机性，您会得到一个秘密的圣诞老人，由于某种原因它不会成为秘密。例如，如果我的圣诞老人是我的妻子，几乎不可能对其保密。

因此，我们决定为该问题添加约束。例如，爱丽丝（Alice）和鲍勃（Bob）登录了活动，但不想互相送礼物。我们需要将此数据添加到算法中并考虑这些约束。我们可以稍微修改一下算法：当我们需要为有约束条件的参与者（例如鲍勃）挑选一个接收者时，我们从参与者池中删除这些约束条件（爱丽丝）并像以前一样随机选择一个。

由于这种限制，我们的幼稚算法在某些情况下可能会失败。如果这是算法的最后一步，我们需要为Bob选择一个接收器，而Alice是池中剩下的唯一选项，该怎么办？在这种情况下，如果我们应用所有约束，将没有可供选择的选项，因此将没有解决方案。

我们该如何解决呢？这里最简单的方法是重新启动算法，直到获得解决方案。如果没有什么限制，那应该很安全。实际上，我们在Web服务的第一个版本中完全采用这种方式进行了修复。它非常适合10位参与者和几个约束，并且一次运行即可找到解决方案。有时需要重新启动1或2次，但是没有无限循环。

但这是我们最初的问题的肮脏解决方案。让我们找到一种可以解决所有输入数据问题的合适算法。可能我们需要使用它的另一种表示形式。

我们有参与者。我们也知道不想互相赠送礼物的参与者的限制（如果有）。当我们有一些对象以及它们之间的联系时，该考虑一下图形了。

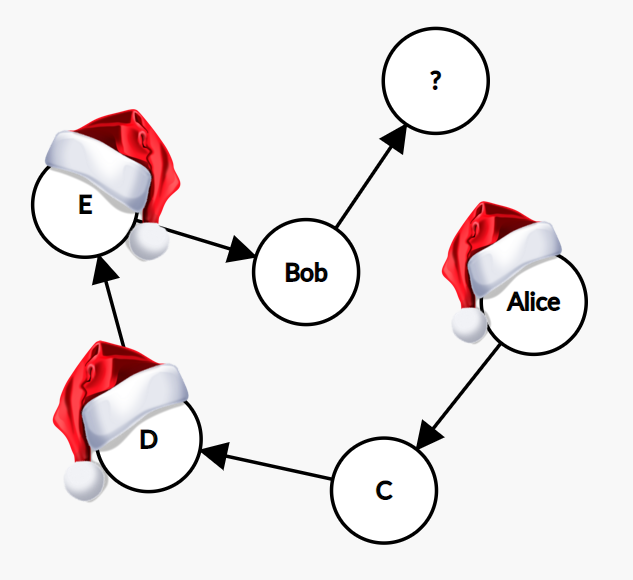
在此图中，节点是参与者，节点之间的连接表明它们可以互相提供礼物。鲍勃和爱丽丝无法做到这一点，因此他们之间没有直接联系。

现在我们可以看到我们的解决方案是该图中的路径。它必须从任何节点开始，然后精确地遍历其他节点一次，然后再回到起点，因此这意味着该路径实际上是一个循环。穿过所有节点的路径曾经被称为哈密顿路径。因此，这种循环是哈密顿循环。

这意味着“秘密圣诞老人问题”基本上是哈密顿循环问题，我们可以在书中或在互联网上找到正确的算法。

但是谷歌令我失望。显然，没有快速算法可以在图中找到哈密顿路径或循环。这是一个NP问题（不确定性多项式），这意味着没有多项式算法。

给定一个城市列表以及每对城市之间的距离，最精确的路线是什么？

听起来很熟悉，不是吗？我们需要访问每个节点一次，然后返回到初始节点。这基本上是我们在这里的哈密顿周期。 TSP没有快速的解决方案。人们撰写有关如何更快解决问题的科学论文。有些使用启发式方法来减少暴力搜索中的选项数量。有些人使用动态编程将其分解为子问题，这些子问题更容易解决。

这是否意味着我们的“秘密圣诞老人问题”需要如此复杂的算法？不，要容易得多。这里的主要区别在于，旅行商问题需要一个最佳的汉密尔顿周期（最短或最有利可图），而秘密圣诞老人问题则需要任何汉密尔顿周期。

为了对TSP进行暴力破解，我们需要找到所有可能的周期并选择最佳周期。可能的循环量是通过阶乘函数计算的：将1到N之间的所有整数相乘。如果图中有5个节点，则将有120个循环要进行蛮力。对于10个节点，将有3628800个选项。 20个节点：2432902008176640000。

我们的问题要简单得多。图中有许多合适的周期，我们需要找到第一个合适的周期。蛮力现在并不那么可怕。

让我们找出算法。我们的目标是使用蛮力在图中找到哈密顿循环。我们从一个随机节点开始。该节点具有一些连接的节点。我们随机选择一个邻居，然后去那里。该节点也已连接节点。我们选择了其中一个尚未被访问的人。等等。

在某些步骤中，我们可以发现没有可供选择的节点。如果没有更多的连接（由于约束）或已经访问了所有邻居节点，则可能会发生这种情况。这个问题看起来像我们在使用朴素算法时遇到的问题。使用图形，可以更清楚地知道我们可以后退一步，然后选择另一个随机节点。如果我们退后一步，但仍然没有要选择的节点，则再退一步。

重复直到访问所有节点并返回第一个节点。循环完成。

如果我们总是发现一个死胡同，并且在多次回溯之后，我们没有找到汉密尔顿周期成功地返回第一个节点，那么该图就没有解决方案。这是最坏的情况，因为我们需要暴力破解所有路径以验证没有合适的循环。还有很多，请记住阶乘函数。

但是，我们正在为特定的Web服务解决“秘密圣诞老人”问题。这实际上是一项工程任务，而不是一项数学任务。如果约束太多，并且图中没有足够的连接来找到合适的循环，则可能会使算法失败。

如果我们举办了“秘密圣诞老人”活动，那将很可疑，一些参与者认为他们不希望将几乎所有其他人都视为圣诞老人。我们可以在界面上添加一些限制，并定义每个参与者最多可以有3个约束。这对于每个人都必须足够，并且将防止该算法强行使用数百万条路径。

我做了一些测试。具有3个约束的算法有时必须进行1或2个回溯，但是在大多数情况下，它会为N个参与者分N个步骤找到解决方案。约束量越大，情况就越糟。例如，有100个参与者，每个参与者有50个约束，蛮力有时需要100步，有时需要400000，有时需要1500000。

我们最初的问题已经解决，并且我们有一个具有稳定排序算法的可运行网络服务。即使有成千上万的参与者，它的运行速度也足够快，这对于家庭聚会活动来说已经足够了。我们了解了有关汉密尔顿周期，NP问题和深度优先回溯搜索的知识。