从1米到Graham的号码（2014年）

上周，我们从1开始，然后逐渐稳定地达到了1,000,000。我们使用了点。好可爱

在一切完全失控之前，让我们首先提高仍然深不可测的10的幂，

当我们从1增长到1,000,000时，我们不需要幂-我们可以使用一小串数字来表示我们所谈论的数字。如果我们想将数字乘以10，我们只需添加一个零即可。

但是随着您前进超过一百万，零开始变得越来越丰富，您需要使用不同的表示法。这就是为什么我们使用权力。当人们谈论指数级增长时，他们指的是当您开始使用力量时可能发生的疯狂行为。例如：

随着我们今天变得越来越大，我们将继续使用10的幂，因为当您开始谈论非常大的数字时，变得有意义的是数字的数目，而不是数字本身。每个70位数字都在10 69到10 70之间，这确实是您需要知道的。因此，至少对于本文的第一部分而言，10的幂可以很好地用作数量级“检查点”。

每次我们将能力提高一倍，我们所处的世界就会乘以十，从而极大地改变事物。让我们从上次停止的地方开始-

10 6（1百万– 1,000,000）–上周完成的那幅巨大图像中的点数量。在我的计算机屏幕上，该图像的面积约为18cm x 450cm = .81 m 2。

10 7（1000万步）–这使我们到达了一个范围，其中包括绕地球行走所需的步数（4000万步）。如果您绕地球的每一个脚步都用一个点表示，例如上一篇文章中的网格，则这些点将填充一个6m x 6m的正方形。

10 8（1亿）–现在我们处于人类历史上已经出版的书籍数量（1.3亿），而在这个范围的顶部，一个人一生中说的估计单词数（8.6亿） 。同样在这个范围内的是赢得真正大彩票的几率。最近的超级百万乐透彩票中奖率为175,711,536分之一。为了把握这些机会，大约是六年中的秒数。因此，这就像知道刺猬在未来六年内只会打喷嚏一次，并将您来之不易的钱花在特定的一秒钟上（例如，2017年3月19日凌晨2:52的第36秒钟），并且只有在恰好在那一刻打喷嚏。不要购买超级百万彩票。

10 9（10亿1 – 1,000,000,000）–这里我们有一个世纪的秒数（大约30亿），有生命的人数（71.25亿），而为了容纳10亿个点，我们的点图像将覆盖两个篮球法院。

10 10（100亿）–现在距离自大爆炸（137亿）以来的岁月还有距耶稣基督活着（600亿）的秒数。

10 11（1000亿）–这是关于银河系中的恒星数和可观测的宇宙中的星系数（100-4000亿），因此，如果一台计算机自基督以来每秒每秒列出一个可观测的星系，则不会目前尚待完成。

10 12（1万亿– 1,000,000,000,000）–百万亿。如果将整个人类放在上面，磅秤将显示的磅数（〜1万亿），人类已经存在的秒数（〜100,000年=〜3万亿秒），并且大于这两个总数的总和一光年的英里数（6万亿）。一兆兆是如此之大，以至于您只需要4万亿毫米的缎带就可以在太阳周围系弓。

10 13（10万亿）–这是我们在现实世界中所讨论的数字所能获得的最大数量，并且几乎总是与国家和美元相关— 2013年美国名义GDP略低于17万亿美元，债务目前不到18万亿美元。这两个数字与人体细胞数量（37万亿）相形见war。

10 14（100万亿）– 100万亿是人类历史上每本已出版书籍中的字母数量，以及您体内的细菌数量。 2同样在这个范围内的是世界总财富（241万亿美元，我们在上一篇文章中进行了详尽的讨论）。

10 15（1 quadrillion）–好的，再见一般的话。人们经常说百万，十亿和万亿这个词。没有人说四方。说“四方”一词真的很酷。 3大多数人改为选择“一亿亿美元”。不管哪种方式，地球上大约有四千万个蚂蚁。将该事实与细菌事实进行比较，就好像您有1/10的全球蚂蚁在体内爬行一样。

10 16（10千万像素）–在这个范围内，我们获得了不小心从桌子上掉下来覆盖整个地球的纸牌数量（89百万像素）。人们会生你的气。

10 17（100万亿次）–自大爆炸以来的秒数。上周进入我的音乐世界的对Kim Kardashian的引用数量也是如此。请住手。

10 18（1 quintillion）–又称十亿美元，“ quintillion”一词的确比“ quadriion”更酷。拥有社交能力的人从来没有说过“五百亿”这个词。无论如何，它是地球上所有海洋中水的立方米数和一粒盐（1.2亿盐）中的原子数。地球上每个海滩上的沙粒数量约为7.5亿五千万，与六个盐粒中的原子数相同。

10 19（10亿五千万）–从此处到最近的下一个恒星的毫米数（38亿五千万毫米）。

10 20（100亿五千万）–步行穿越整个银河系所需的米长步数。这么多播客。听说普朗克书吗？这是科学家们谈论的最小体积，所以小到可以在一个质子中容纳100亿个质子。稍后更多关于普朗克卷的信息。哦，还有我们的点像？当我们达到600亿个点时，图像将覆盖地球表面。

10 21（1亿分之一）–现在，我们甚至超出了怪胎的词汇范围。我认为我从未听过有人大声说“ sextillion”，我希望保持这种状态。

10 23（100亿亿）–粗略估计可观测宇宙中的恒星数量。在高中时，您还必须处理这个数字-602兆，即6.02 x 10 23-是一个摩尔数，即Avogadro数，以克为单位的氢原子数。

10 25（9月10日）–世界所有海洋中的水滴数。

10 27（1 oct）-如果地球是空心的，则需要1 oct豌豆将其装满。而且我想我们已经从八百万听来了差不多。

好吧，现在让我们向前迈进一大步，进入一个完全不同的领域，即地球体积太小而宇宙大爆炸太新而无法在示例中使用的地方。在这个崭新的数字舞台上，只有可观察的宇宙（一个大约920亿光年的球体）可以处理我们正在处理的规模。 4 10 80 –要达到10 80，您需要乘以一万亿，再乘以一万亿，一万亿，一万亿，一万亿，一万亿，一亿。没有出售此编号的圆点海报。那么，为什么我在这里停下来呢？因为这是对宇宙中原子数的普遍估计。

10 86 –如果您想用豌豆包裹整个可观测的宇宙球，该怎么办？您需要10 86粒豌豆才能实现这一目标。

10 90 –这是将整个宇宙充满要用多少个中等大小的沙粒（直径0.5毫米）。

当美国数学家爱德华·卡斯纳（Edward Kasner）于1938年有一天变得可爱，并要求他9岁的侄子米尔顿（Milton）提出10 100-1（带100个零）的名字时，便使用了googol。弥尔顿（9岁）是个精神错乱的人，他建议说“ googol”。卡斯纳显然​​认为这是一个合理的答案，然后就回答了，就是这样。 5这是可以容纳在宇宙中的沙粒数量乘以100亿。因此，想象一下充满小颗粒沙子的宇宙-在地球上方，下方，前方，下方的沙子中仅数百亿光年。无尽的沙子。您可以在任何方向上全速飞行飞机数万亿年，而您将永远无法走到尽头。很多很多很多的沙子。

现在想象一下，您将飞机停在某个点，伸出窗户，然后在强大的显微镜下抓起一粒沙子来观察—并且您看到的实际上不是单个颗粒，而是包裹了100亿个微观颗粒膜，所有这些都等于一块普通沙子的大小。如果在这种假设中每个沙粒都属于这种情况（如果每个沙粒实际上都是一捆100亿个微小的沙粒），那么这些细沙粒的总数就是googol。

为了使这些数字适应物理世界，我们在大小事情上都没有足够的空间，但还有三个适合您：

10 113 –将宇宙充满其中所需要的氢原子数。

10 185 –回到“普朗克”册（我所听说过的在科学界讨论过的最小册）。您可以在最大的事物（可观察的宇宙）中容纳多少这些最小的事物？ 10 185.在两端都不能变小或变大的情况下，我们已经达到可以使用物理世界对其进行可视化的最大数量。

在将新命名的googol普及之后，Krasner几乎不能再穿上这只可爱的新schtick，并要求他的侄子再创造一个名词。在Milton张开嘴巴并宣布数字googolplex之前，他几乎无法解决问题，他以典型的Milton形式描述为“ 1，然后写零直到您累了”。 6此时，克拉斯纳表现出了一些反常的束缚，无视米尔顿，给了这个数字一个实际的定义：10个googol或1个，后面写了一个googol零。具有完整的写出指数，googolplex看起来像这样：

因此，googol为1，其后仅100个零，这比填充宇宙的沙粒大100亿倍。您是否可以想象将googol零放在1后面会产生什么样的数字？

没有可能的方式将头部包裹在该号码周围 - 我们能做的最好的就是尝试了解写数字需要多长时间。我上面写的是什么只是指数 - 实际上写一个Googolplex out涉及写一个googol zeros。首先，让我们弄清楚我们写下这些零的地方。

正如我们所讨论的，用沙子填充宇宙只会让你成为一个歌唱者的十亿亿道路，所以我们要做的就是用沙子填充宇宙，得到一个非常小的笔，写作每粒沙子上的10亿零。如果你这样做，然后在显微镜下看过一个完成的谷物，你会看到它覆盖了100亿微观零。如果你这样做，在每一粒灌装宇宙的沙子上，你已经成功地写下了数字googolplex。

好吧，我刚刚测试了人类可以合理地编写零的速度有多快，我在10秒内写了36个零。 7，如果从5到85岁到85岁，我每天26小时，每天都在为期16个小时，就在这个速度上写零，我在我的一片沙子上完成了一半的沙子一生。你需要奉献两个完整的人类生活，以完成一粒沙子。大约1070亿人在物种的历史中生活过。如果每个人都致力于他们生命的每一个醒着的时刻，就像在沙粒上写零，因为我们现在的物种填满了一侧的立方体，围绕着人类完成的砂粒的高度。而已。

现在，在实际数字的阶段是多大的瞥见 - 随着WherePhilers解释，可能在人类占用的空间中可能出现的总量子状态（即，在该空间中可能发生的原子的每个可能的原子排列）都远远少而不是一个googolplex。这意味着，如果有一个宇宙的宇宙，那么戈戈尔霍姆拉立方米（一个非常大的空间），随机概率表明，你会在那位宇宙中有精确的副本。为什么？因为在人类大小的空间中的所有可能的物质安排都会发生很多，但许多次在一个巨大的空间中，这意味着可能存在的一切都存在 - 包括你。包括猫须但正常的猫须。包括你但是一英尺高的版本。包括你的左手上的是你的左手，你的左手是拿破仑的阴茎作为你的第五根。我所说的不是科幻小说 - 这是一个大的空间的现实。

你知道有时候你有多经历生活，而且你迷失了，但你甚至不知道，然后有一天，合适的人来了，你意识到你一直在寻找什么？

巨大的数字一直都吩咐我，给了我噩梦，直到​​我了解了Graham的号码，我以为人类最大的数字可以设想是“一个歌唱者对歌唱者的歌唱者”，这将在我兴起我的思想想到它。但是当我了解到Graham的号码时，我意识到，不仅我没有划伤了真正巨大的数字的表面，我就无法这样做 - 我没有工具。而现在我已经获得了那些工具（你今天也将来），一个Googolplexth权力的歌唱者听起来像个孩子说“100加100！”。当被要求说他能想到的最大数字。

在我们潜入之前，为什么格雷厄姆的号码甚至是一个人谈论？

我不会真正解释这个问题，因为解释的确很无聊和令人困惑-这是罗纳德·格雷厄姆（现任美国数学家）提出的官方问题：

连接n维超立方体的每对几何顶点，以获得2 n个顶点的完整图形。将此图的每个边缘上色为红色或蓝色。每个这样的着色在四个共面顶点上包含至少一个单色完整子图的n的最小值是多少？

我告诉你这很无聊和令人困惑。无论如何，对这个问题没有唯一的答案，但是格雷厄姆的证明包括上下限，而格雷厄姆的数字是格雷厄姆想出的上限n的一种形式。

他在1977年提出了这个数字，当一位同事在《科学美国人》上写下该数字时，它得到了认可，并称其为“范围如此之大，以至于它拥有有史以来最大数量的数字记录，这是认真的数学证明。”出于同样的原因，这个数字最终在1980年被《吉尼斯世界纪录》收录，尽管今天已经超过了它，但它仍然是大多数人听说过的最大数字而闻名。因此，格雷厄姆（Graham）的数字是一件事-它不仅是一个任意大的数字，而且实际上与数学世界相关。

因此，无论如何，我上面说过，由于缺乏工具，我在数量上甚至还无法想象，所以我受到了限制-那么我们需要什么工具呢？

超运算序列是一系列数学运算（例如加法，乘法等），其中序列中的每个运算都是从前一个运算开始的迭代。一秒钟您会明白的。让我们从第一个也是最简单的操作开始：计数。

如果我有3个，并且我想从那里爬上去，那么我会走3、4、5、6、7等，直到到达想要的位置。不是大功率的操作。

加法是从计数开始的迭代，我们可以将其称为“迭代计数”，因此，我只能说3 + 4而不是3、4、5、6、7，直接跳到7。加法是“迭代计数”意味着加法就像是计数捷径，是将所有计数步骤捆绑为一个更简洁的步骤的方法。

上一级，乘法是迭代加法-加法捷径。与其说3 + 3 + 3 + 3，不如说是乘法，我们可以将所有这些加法步骤捆绑为一个更高的运算步骤，并说3 x4。乘法比加法更强大，您可以用它创建更大的数字。如果我将两个八位数字加在一起，最终将得到一个八位或九位数字。但是，如果我将两个八位数字相乘，最终得到的是15位或16位数字-更大了。

再上一层，求幂是迭代乘法。求幂运算无需说3 x 3 x 3 x 3，而是将字符串捆绑为更简洁的3 4。

现在，事实是，这是大多数人停止的地方。在现实世界中，幂运算是我们在超操作序列中倾向于使用的最高操作。当我构想出巨大的googolplex googolplex数时，我正在尽我所能使用我所知道的最高水平-求幂。在级别3上，尽可能大的方法是使基数大且指数数大。一旦做到这一点，我就筋疲力尽了。

突破数量上限的关键是要了解您可以提高操作水平，您可以无限地进行迭代。这就是数字变得真正庞大的方式。

为此，我们需要一种不同的表示法。到目前为止，我们在每个级别上都使用了不同的符号（+，x和上标），但是如果我们要使用大量的符号，我们不想记住很多不同的符号不同的操作级别。因此，我们将使用Knuth的向上箭头表示法，该符号可以在任何级别上使用。

Knuth的向上箭头表示法从操作级别3开始，用单个向上箭头↑代替了幂运算。因此，使用向上箭头表示法，而不是说3↑4，而是说3↑4，但是它们的含义相同。

3↑4 = 81 2↑3 = 8 5↑5 = 3,125 1↑38 = 1

现在，让我们上一个台阶，开始了解超操作序列的疯狂力量：

Tetration是迭代取幂。在我们了解如何以幂运算方式将乘法运算符串捆绑幂运算字符串之前，我们需要了解什么是“幂运算符串”。

到目前为止，我们对乘幂所做的只是一个计算-一个基数和它的乘幂。但是，如果我们将其中两个计算放在一起怎么办，例如：

我们得到了一座电力塔。电力塔的功能强大到令人难以置信，因为它们从顶部开始，一直向下移动。所以2 2 2 = 2（2 2）= 2 4 = 16。

使用括号强调自上而下的顺序：3 3 3 3 = 3 3（3 3）= 3 3 27 = 3（3 27）= 3 7,625,597,484,987 =一个3.6万亿数字

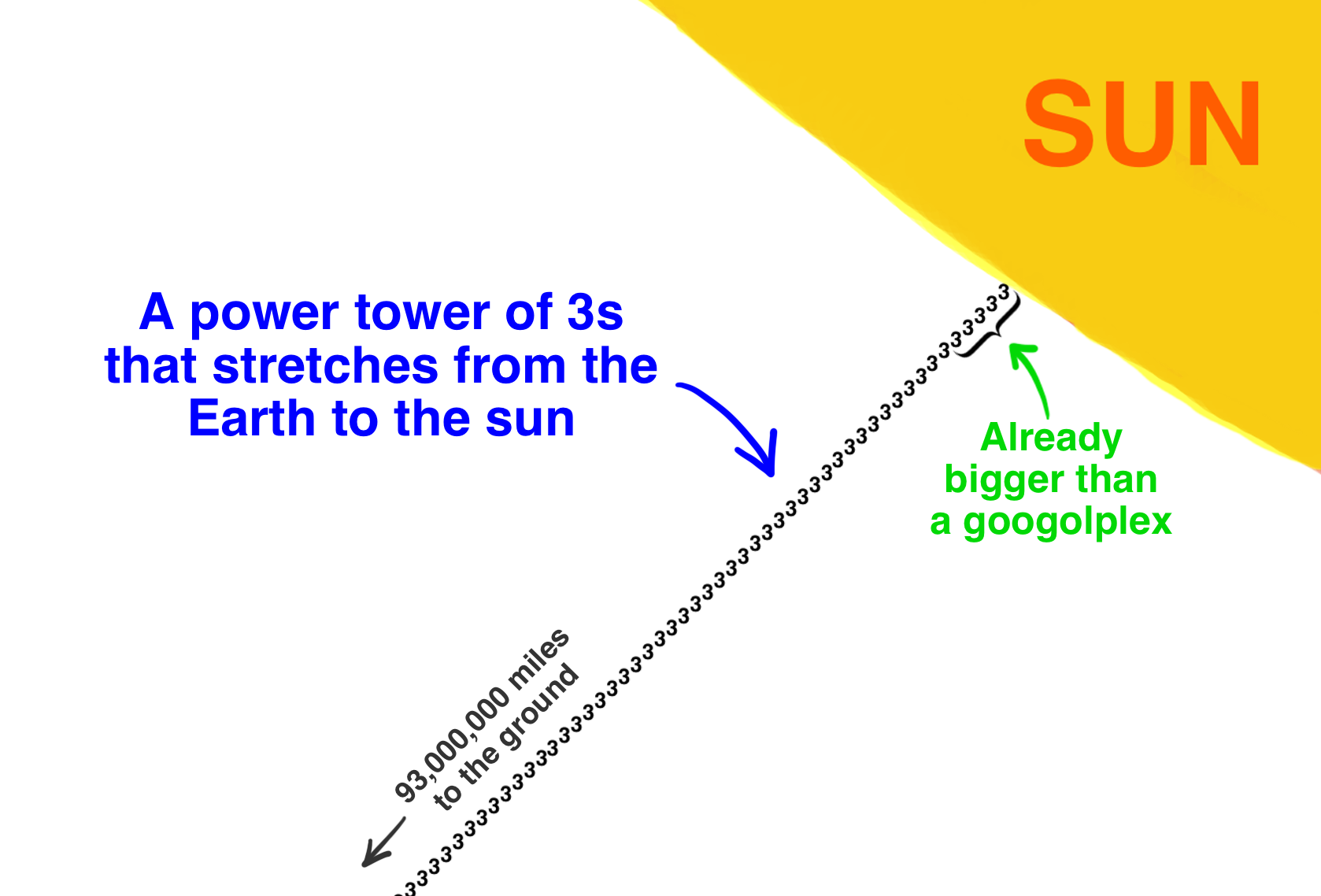
请记住，googol及其充满宇宙的微观迷你沙仅仅是100位数字。因此，仅需一个3s的电力塔，即可堆叠4个高点，以使googol相形见10，还有10 185个普朗克体积足以填充整个宇宙和我们的物理世界。它没有googolplex一样大，但我们可以通过在堆栈中再添加3个来轻松解决：

3 3 3 3 3 = 3（3 3 3 3）= 3（3.6万亿数字）=比googolplex（10（100数字））大得多。 对于googolplex本身，电力塔使我们可以通过将其编写为： 10 10 100，或更典型的是10 10 102。因此，您可以想象一下开始建造高功率塔时会得到什么样的数字。 眼神激烈。 现在这些塔是3级指数字符串，就像3 x 3 x 3 x 3是2级乘法字符串一样。 我们使用Level 3将Level 2字符串捆绑为3 4或3↑4。那么，如何使用Level 4捆绑指数字符串呢？ 双箭头。 3 3 3 3与说3↑（3↑（3↑3））相同。 我们将这4个单箭头3捆绑为3↑↑4。 同样，3↑↑5 = 3↑（3↑（3↑（3↑3）））= 3 3 3 3 3 4↑↑7 = 4↑（4↑（4↑（4↑（4↑（4↑4）））））=一个力量塔 ......