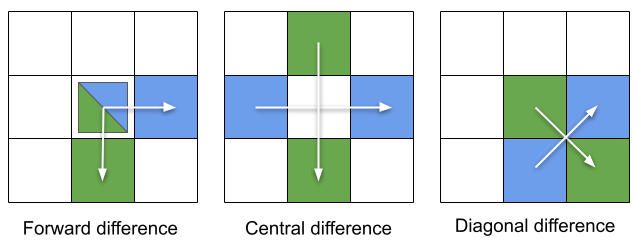
像素/体素网格上的渐变–前向，中央和对角线差异

在本文中，我将重点介绍计算机图形学和图像处理中定义在网格上的图像信号的梯度。具体来说，是将图像的梯度/导数，高度场，距离场表示为离散的，均匀的像素或体素网格。

我将从最基本的内容开始-梯度通常是什么意思（因为它并不总是“标准化”的），它们的用途是什么，典型的方法（正向或中心差异）是什么，它们的利弊是什么，以及然后继续讨论一个具有非常好的属性的有趣替代方法-对角渐变。

我的文章将以如何在简单有效的方案中实际使用它们的建议作为结尾，以及如何通过少量的计算将其扩展为结构张量的超级有用的概念，该结构张量可以表征任何梯度场的主导方向，并完成带来一些信号处理乐趣–前向和中央差异的频域分析。

对于离散信号来说，这并不是一个很好定义的问题，但是最常见和最有用的思考方式是受信号处理和采样思想的启发：

假设存在一些离散的连续信号，那么在梯度评估点上，该连续信号的空间维数将是偏导数？

这种解释对于计算机图形学（我们可能对连续曲面进行离散化描述；例如体素场，高度图或距离场）以及图像处理（我们通常认为图像是“自然图像”）都非常有用。拍下）。

用于过程SDF的法线之类的连续渐变和导数也很有趣，但情况有所不同。我不会在这里介绍这些内容，而是建议您阅读Inigo Quilez的这篇很棒的文章，其中包含许多实用技巧（重新阅读我从四面体技巧中学到的技巧）和建议。我相信，无论您对本主题的熟悉程度如何，您都会学到一些新东西。

在我的帖子中，我将重点介绍计算机图形学，图像处理以及解决该问题的基本信号处理。我个人之间并没有进行过多的深层次的联系。因此，我希望我将来能扩展自己的知识，同时也鼓励我的读者探索它：

进一步阅读一个：第一个关系是偏微分方程及其离散化。解决PDE和解决离散PDE是许多专业科学领域都需要解决的问题，计算梯度是数字离散PDE解决方案的固有部分。我对此不太了解，但是我敢肯定文学会对此进行详细介绍。

进一步阅读二：第二个连接是小波，滤波器组以及频率精度/定位权衡。这是在通信理论，电气工程，雷达系统，音频系统等中使用的东西。当我阅读并熟悉一些理论时，我在工作中没有发现太多小波的实际用途（除了最简单的Gabor或用于图像金字塔的小波），所以我再次向您推荐一些更专业的小波读。

计算表面法线-当我们具有标量场之类的东西时-无论是描述底层隐式表面的距离场还是仅是高度场，我们可能要计算其梯度以计算表面法线或法线贴图的高度场，评估BRDF和照明等。甚至可以用于地形上的物理模拟，碰撞或动画！

查找边缘，不连续性，拐角和图像特征–我将重点关注的另一个应用程序是简单地找到图像特征，例如边缘，拐角，“细节”或纹理区域；信号变化并变得更加“有趣”的区域。人类视觉系统实际上是由许多边缘检测器和局部微分器构建而成的，可以看作是多尺度的时空梯度分析仪！这是出于生物学动机–当信号在空间或时间上发生变化时，这意味着它是潜在的兴趣点或威胁。

仅计算梯度的额外用例就是找到这些特征的方向和描述。这是任何图像处理的基础，但在计算机图形学中也很常见-从形态学抗锯齿，选择性地仅对边缘进行超采样或特殊效果。我将在“结构张量”部分中对局部特征的描述中再次进行介绍，但现在让我们使用最常见的应用程序–仅使用梯度矢量幅度，例如在Sobel运算符中使用的。

西门子之星–一种测试模式，可用于测试不同的“角度”和不同的频率，

以16倍分辨率渲染Siemens星，并使用尖锐的抗混叠滤波器（带窗的sinc）进行降采样。中间有一些混叠，但是对于我们的用例来说是可以的（我们希望在那里看到一个急剧的信号变化然后检测出来）。

我喜欢这个解决方案的地方在于它既直观，天真又具有理论上的动机！我不想改写维基百科，并且我博客的大多数读者都不太在乎形式证明，因此随时可以在那里查看或参加专门课程（旁注：2010年代+很棒，有很多最好的教授在互联网上公开分享他们的课程幻灯片…）。它基本上是围绕f（x + 1）– f（x）的泰勒展开建立的。

此差分算子与使用[-1，1]滤波器对图像进行卷积相同。

这很容易，运作得相当好，很有用。但是有两个更大的问题。

如果您已经阅读了我以前的博客文章-关于双线性下采样/上采样-可能马上就会看到挑战之一。与偶数大小的滤镜卷积，将整个图像移动半个像素。

根据应用程序的不同，这可能是一个问题。 “解决方案”很简单–用另一个大小相等的过滤器将其撤消。完美的解决方案将是重采样，但是以半像素进行重采样却具有令人惊讶的挑战（请参阅我的另一篇博客文章），因此我们可以使用对称滤镜对其进行模糊处理。模糊梯度大小可以解决此问题（以模糊为代价）：

使用均匀大小的滤镜进行模糊处理可以固定均匀大小的偏移。但是另一个问题现在可能已经变得更加明显。

注意：您可能想知道，如果我们仅模糊部分差异，会发生什么？我们将在一秒钟内看到。

第二个问题更加严重。如果我们计算多个偏导数会怎样？像df / dx和df / dy这样吗？

现在，让我们再次看看同一幅图，这次重点是“对称性”。这说明了为什么这是一个现实的问题，而不仅仅是理论上的问题。如果我们看西门子星和盒子的梯度，我们会发现一些不对称性：

这绝对不好，并且会在图像处理或计算法线中引起问题，但是如果我们查看图像中心的简单“正方形”的梯度大小，则情况更糟–请注意图像拐角处（一个拐角处）发生了什么被切断，另外一个2倍太紧！

对于任何实际应用程序来说，这都是一个大问题。我们需要研究更好的近似值。

我提到“模糊”偏导数可以使它们“居中”，对吗？如果我告诉您它在数值上也更准确怎么办？这就是所谓的中心差异。

由评估。除以2很重要，直观上可以理解为除以像素之间的距离或差分dx，其中dx大2倍。

当前向差是近似于O（h）的近似值时，该近似值更近似于O（h ^ 2）。我不会在这里解释这些术语，但是维基百科有一些基本的介绍，在数值方法文献中，您可以找到更详细的解释。

这也等效于用[0.5，0.5]滤波器“模糊”正向差异！ [0.5，0.5] o [-1，1]导致[-0.5，0，0.5]。最初，我对这种联系感到非常惊讶-更精确，理论上有动机的泰勒展开，以及“一些随机的临时实践模糊”。这甚至是大小上的模糊，因此这也解决了半像素偏移问题并使两个偏导数正确居中：

但是，还有另一个问题。请注意，像素上的梯度估算完全没有考虑像素的值！这意味着像0 1 0 1 0 1这样的模式将具有…零梯度！

这就是两种方法在所有梯度（包括“条纹”图案）上进行比较的方式：

中心差可预测任何类似于1 0 1 0的最高频率（奈奎斯特（Nyquist））序列的零梯度！在西门子星上，正好在中心以外显示为缺少/零梯度。

我们知道那里有很强的渐变色，还有很强的图案/边缘，所以这显然是不对的。

这可能会并会导致一些严重的问题。如果我们看西门子星，我们会注意到它很好地对称，但是却错过了中心的梯度信息……

这里值得一提的是什么是常用的Sobel滤波器。 Sobel滤波器无非是在垂直于评估梯度的方向上被模糊（具有高斯二项式滤波器近似）的中心差所引起的，所以类似：

在Sobel滤波器中进行此操作的实际动机是：a）滤除一些噪声和对不太明显的单个像素渐变敏感的趋势，更重要的是b）它的模糊引入了更多的“各向同性”行为（您将在下面看到“对角线”和“角线”的幅度更接近水平/垂直边缘）。

Sobel运算符将与中心差异进行比较（比较相似度最大的差异）：

在网格上提到各向同性或各向异性响应对我来说总是很奇怪。为什么？因为奈奎斯特频率不是各向同性或径向的，所以它们形成一个盒子。这意味着我们可以在对角线上代表比主轴更高的频率。我在我的较早的文章中介绍了如何通过旋转示例网格（例如在许多Playstation 4 Pro中使用此属性以时空上采样来实现4K渲染）在棋盘格渲染中使用此属性。但是任何分析都变得“怪异”，我经常看到关于可分离Sinc是否是“最佳”图像滤波器的讨论，而不是旋转对称Jinc。

对于图像渐变的重要性，我没有一个简单的答案，问题是“取决于”。您是否关心将较高频率的对角线梯度检测为较强的梯度？用例是什么？在法线贴图的背景下，我还没有考虑过这一点，因为这可能会导致“怪异”的曲率，但我不确定。出于个人好奇心，我可能会在某些时候再次提及它，因此请在评论中让我知道您的想法和/或经历。

请注意，由于您可以使用中心差来提高前向差/高阶近似的精度，因此您可以走得更远，在派生近似滤波器中添加更多抽头！

它们可以帮助消除高频梯度，但是您的梯度在空间中的位置越来越少。这是我提到的与小波，音频，STFT和其他区域的连接。

我还喜欢直观地将其视为[-1，1]滤镜的半像素重采样。 🙂例如，如果您要对[-1，1]进行重新采样，并移动较大的sinc滤镜半个像素，则会得到类似的行为：

在所有这些背景下，现在是该帖子的主要建议的时候了。

这是我从BLADE项目的同事那里学到的（使用离散的学习滤镜近似图像操作），然后我们在工作中使用了手持多帧超分辨率纸和Super-Res Zoom Pixel 3项目。我很高兴领导。

在一些电子邮件中，我也对本文的这一部分有很多疑问，所以我认为这不是一个非常普遍的“技巧”。如果您知道它的起源和使用它的域越来越多，请告诉我。

编辑：唐·威廉姆森（Don Williamson）在推特上注意到它的名字叫罗伯特·克罗斯（Robert’s Cross），它是1963年开发的！

这里的想法是计算对角线上的梯度。例如在2D中（请注意，它会扩展到更高的尺寸！）：

我们可以看到，在对角线差的情况下，两个偏导数近似值都位于同一点的中心。我们像前向差一样计算它们，但是需要补偿更大的距离，sqrt（2），像素对角线的大小，所以和。

如果使用这样的渐变，则可以“旋转”法线。对于梯度幅度，您无需执行任何特殊操作，它的计算方法相同（向量的长度）！

这样计算出来的梯度不会缺少高频梯度问题；也不存在不对称问题：

它具有像素偏移和某些各向异性的问题，但是像素偏移可以很容易地固定。

这意味着将所有平方梯度求和，然后除以4（梯度对的数量），这都是非常有效的操作。然后，您只需取平方根并获得梯度量值。

这解决了相移问题，而IMO是迄今为止讨论的所有替代方案中最好的：

对角线差异可以正确检测高频，不存在像素偏移问题，尽管它们表现出完美的各向同性，但实际上通常“足够好”。

一方面有些模糊会降低“定位”，但另一方面这可能是理想的，它可以提高对噪声和单个像素渐变的鲁棒性。

仅需几行代码（以及一些额外的计算……），我们就可以从中提取更多信息！

我们有一堆像素的“袋”或梯度值……如果我们试图找到“附近的主要梯度方向是什么”的最小二乘解，该怎么办？

我在数学推导方面并不擅长，但这是对结构张量的优雅解释。结构张量是梯度的Gram矩阵（“堆叠”梯度的矢量乘以其转置）。

许多困难的单词，但从本质上讲，它是一个非常简单的2×2矩阵，其中的条目是dx ^ 2，dy ^ 2在对角线上的平均值和dx * dy在非对角线上的平均值：

现在，如果我们对该矩阵进行特征分解（对于Gram矩阵始终是可能的–对称，正半定数），我们将得到以下简单的特征值封闭形式：

您可能要对向量进行归一化；在非对角线Gram矩阵项为零的情况下，特征向量仅是坐标系主轴（1、0）和（0、1）（尽管在这种情况下，请务必对它们进行“排序”，对于欠定系统也是如此） ，顺序无关紧要。

较大的特征值和相关的特征向量描述了主导方向上梯度的方向和大小；它既为我们提供了方向，又为我们提供了该特定方向上的渐变强度。

第二个较小的特征值和垂直的第二个特征向量为我们提供了有关垂直方向上的梯度的信息。

在一起这真的很酷，因为它使我们能够区分边缘，拐角，具有纹理的区域以及边缘的方向。在我们的《手持式多帧超分辨率》论文中，我们使用了两个“派生”属性-强度（仅是结构张量主导特征值的平方根）描述了局部梯度的强度，而相干性计算为。 （注意：论文的原始版本在连贯性的定义上有误，这是由于我们错过了对相机准备好的版本的后期编辑而导致的结果。该值必须在0到1之间）。

连贯性不常见。它描述了主导方向比垂直方向强多少。

通过分析特征向量（由于它们是垂直的，它们中的任何一个都是很好的），我们可以获得有关主导梯度方向的信息。

在我们的测试信号由简单频率组成的情况下，这些信号如下所示（在我快速而肮脏的实现中，请忽略图像之间的边界/边界上的行为）：

这是实际图像上的其他示例，通常使用重映射来显示矢量-由角度定义的色相，由梯度强度定义的饱和度：

这样的分析对于边缘感知的非线性图像处理以及计算机视觉都非常重要。结构张量是Harris角点检测器的一部分，它曾经是整个深度学习革命之前最常见的计算机视觉问题。 🙂（不过，即使您今天仍在实地寻找工作，我还是建议您不要跳过一些基本知识，因为面试官仍然可以要求采用经典方法来验证您了解多少背景知识！）

值得一提的是如何从对角线渐变“固定”结构张量的旋转。如果通过arctan计算角度，这不是您关心的问题（只需为角度添加值），但是在需要更高计算效率的情况下，您不需要进行任何反三角运算，并且至关重要。幸运的是，旋转Gram或协方差矩阵非常简单！旋转协方差矩阵的公式很简单。从角度公式以45度构造旋转矩阵，我们首先得到：

（注意：值得仔细检查一下我的数学。但是，具有完全相同的4个对角线元素会取消它们，并建议使用仅垂直或仅对角线渐变！）

在结束本文之前，我不禁从信号处理的角度比较前向差异和中心差异。

这可能有点不合常规，并且大多数人不是这样看的，但是我不能停止思考高频消失的问题。当频率达到无穷大时，理想的连续信号微分器应具有“无限”的频率响应！

显然，在离散域中，频率只能上升到奈奎斯特。但是，让我们看一下前向差分卷积滤波器的频率响应和中心差分：

中央差分卷积滤波器在Nyquist处的频率响应为零，并且似乎比简单的前向差分滤波器随频率增加而使频率响应更差。这是我们为补偿相移而付出的“成本”。

但是给定该频率响应，有意义的是完全“消失”了一个1 0 1 0序列，正好在奈奎斯特（Nyquist），响应为零！

最后，如果我们查看更高阶/更多阶的滤波器抽头梯度近似值，我们可以看到它对于大多数中高频肯定有所改善，但是接近奈奎斯特时的行为仍然是一个问题：

好的，通过9次抽头，我们将获得越来越好的性能，并且更加接近微分线。

同时，收敛速度很慢，我们将无法恢复确切的奈奎斯特：

这是由于在Nyquist的频率响应为0的“完美”重采样所致。这是否是一个问题取决于您的用例。在摄影以及计算机图形学中，我们都获得了发生在完美奈奎斯特上的序列（通过光栅化或采样摄影信号）。无论如何，我强烈建议您不要使用对角线滤镜！

在我的帖子中，我只浏览了网格（图像，体素）渐变的深层主题，但涵盖了一系列相关主题和联系：

我讨论了前向差异和中央差异之间的差异，如何解决它们的一些问题，以及使用经典Sobel算子的一些原因。

我提出了使用对角线渐变的巧妙“技巧”，可解决其他替代方式的一些缺点，并建议您使用它。尝试使用其他信号源（例如体素），或用于

......