听到鼓的形状

跳转到导航跳转到搜索听到鼓的形状就是通过使用数学理论从它发出的声音（即从泛音列表中）推断出鼓头形状的信息。

＆＃34;可以听到鼓的形状吗？＆＃34;是Mark Kac在1966年《美国数学月刊》上发表的一篇文章的标题，该问题使这个问题闻名，尽管这一措辞源自Lipman Bers。类似的问题可以追溯到Hermann Weyl [需要引用]。 Kac的论文获得1967年的Lester R. Ford奖和1968年的Chauvenet奖。[1]

鼓面可以振动的频率取决于其形状。如果形状已知，则亥姆霍兹方程计算频率。这些频率是空间中拉普拉斯算子的特征值。一个中心问题是，如果频率已知，形状是否可以预测？例如，是否可以以此方式识别圆形三角形。 [2]卡克（Kac）承认他不知道两个不同形状是否可能产生相同的频率集。频率是否决定形状的问题最终在1990年代初由Gordon，Webb和Wolpert否定。

更正式地说，鼓被认为是弹性膜，其边界被夹紧。它在平面中表示为域D。用λn表示D的Dirichlet特征值：即拉普拉斯算子Dirichlet问题的特征值：

{Δu +λu = 0 u | ∂D = 0 {\ displaystyle {\ begin {cases} \ Delta u + \ lambda u = 0 \\ u | _ {\ partial D} = 0 \ end {cases}}}

如果两个域具有相同的特征值，则称为等谱（或同音）。术语“谐音”之所以合理是因为Dirichlet特征值恰好是鼓能够产生的基本音调：它们自然地以傅立叶系数的形式出现在具有固定边界的解波方程中。

因此，可以将问题重新表述为：如果仅知道λn的值，可以从D推论出什么？或者，更具体地说：是否有两个不同的域是等光谱的？

可以为高维区域或黎曼流形上的拉普拉斯算子的Dirichlet问题，以及诸如Cauchy–Riemann算子或Dirac算子的其他椭圆微分算子的Dirichlet问题提出相关问题。可以施加除Dirichlet条件之外的其他边界条件，例如Neumann边界条件。请参阅光谱几何和等光谱作为相关文章。

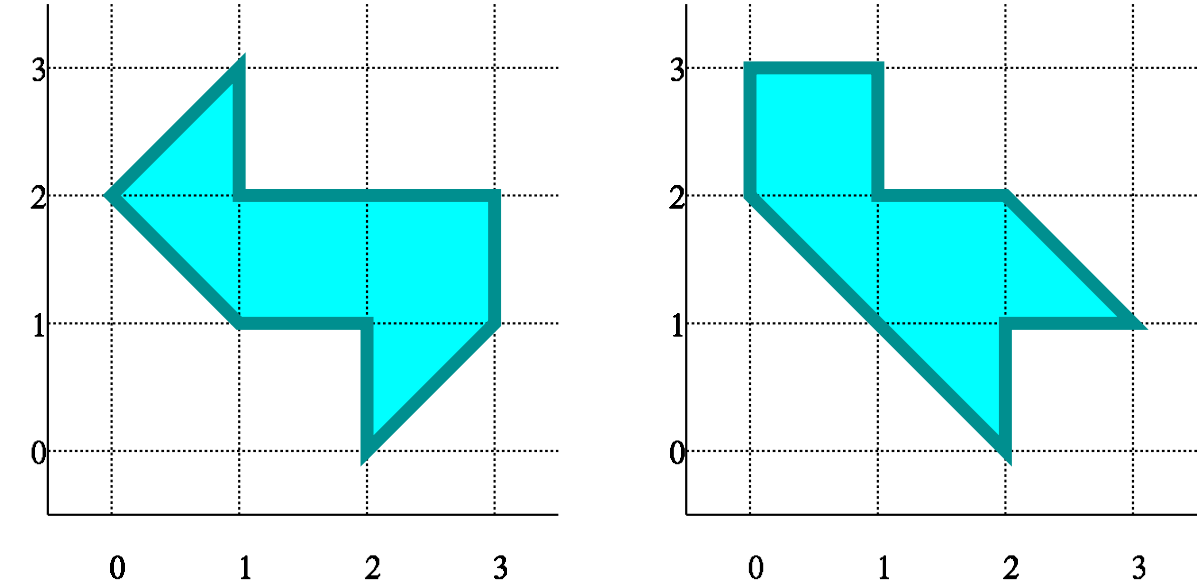
几乎很快，约翰·米尔诺（John Milnor）观察到因恩斯特·维特（Ernst Witt）引起的一个定理暗示存在一对具有相同特征值但形状不同的16维花托。但是，二维问题一直存在，直到1992年Carolyn Gordon，David Webb和Scott Wolpert基于Sunada方法构造了平面中形状不同但特征值相同的一对区域。这些区域是凹多边形。两个区域具有相同特征值的证明使用拉普拉斯算子的对称性。 Buser等人推广了这个想法，他构造了许多类似的示例。因此，对Kac问题的答案是：对于许多形状，人们无法完全听到鼓的形状。但是，可以推断出一些信息。

另一方面，史蒂夫·扎尔迪奇（Steve Zelditch）证明，如果对具有解析边界的某些凸平面区域施加限制，对Kac问题的答案是肯定的。尚不知道两个非凸分析域是否可以具有相同的特征值。已知在C∞拓扑中具有给定等值的一组域是紧凑的。而且，根据Cheng的特征值比较定理，该球体（例如）是光谱刚性的。还通过Osgood，Phillips和Sarnak的结果知道，给定属的Riemann表面的模量空间不允许任何点连续的等谱流，并且在Fréchet-Schwartz拓扑中是紧凑的。

Weyl的公式指出，可以通过计算λn的增长速度来推断鼓的面积A。我们将N（R）定义为小于R的特征值数量，得到

A =ωd − 1（2π）d lim R→∞N（R）R d / 2 {\ displaystyle A = \ omega _ {d} ^ {-1}（2 \ pi）^ {d} \ lim _ {R \ to \ infty} {\ frac {N（R）} {R ^ {d / 2}}} \，}

其中d是尺寸，ωd {\ displaystyle \ omega _ {d}}是d维单位球的体积。 Weyl还推测，下面近似中的下一项将给出D的周长。换句话说，如果L表示周长（或更高维的表面积），则应具有

N（R）=（2π）-dωd AR d / 2 + 1 4（2π）-d + 1ωd-1 LR（d-1）/ 2 + o（R（d-1）/ 2）。 {\ displaystyle \，N（R）=（2 \ pi）^ {-d} \ omega _ {d} AR ^ {d / 2} + {\ frac {1} {4}}（2 \ pi）^ {-d + 1} \ omega _ {d-1} LR ^ {（d-1）/ 2} + o（R ^ {（d-1）/ 2}）。\，}

对于光滑的边界，这是由Victor Ivrii在1980年证明的。流形也不允许具有周期球测地线的两个参数族，例如球体。

对于非平滑边界，Michael Berry于1979年猜想校正应为

其中D是边界的Hausdorff维数。 J. Brossard和R. A. Carmona对此进行了反驳，然后他们建议用上盒尺寸代替Hausdorff尺寸。在飞机上，如果边界的尺寸为1（1993年），则证明了这一点，但对于较高的尺寸（1996年），大多数情况则不予证明。这两个结果均来自Lapidus和Pomerance。

^ Arrighetti，W .; Gerosa，G。（2005）。您能听到鼓的分形维数吗？意大利的应用数学和工业数学。应用科学数学进展丛书。 69.世界科学。第65–75页。 arXiv：math.SP / 0503748。 doi：10.1142 / 9789812701817_0007。 ISBN 978-981-256-368-2。

威廉·阿比科夫（Abikoff，William，1995年1月），《记住利普曼·伯斯》 （PDF），AMS通告，42（1）：8–18

布罗萨德（Jean Brossard）；卡莫纳，雷内（1986）。 ＆＃34;可以听到分形的维数吗？通讯数学。物理104（1）：103-122。 Bibcode：1986CMaPh.104..103B。 doi：10.1007 / BF01210795。

彼得·布什（Buster）；约翰·康威；彼得·道尔； Semmler，Klaus-Dieter（1994），《一些平面等光谱域》，《国际数学研究通告》，第9期：391ff

查普曼（1995）。 ＆＃34;鼓音相同。美国数学月刊。 102（2月）：124-138。 doi：10.2307 / 2975346。 JSTOR 2975346。

奥洛维耶（Olivier）吉罗（Giraud）； Thas Koen（2010）。 ＆＃34;鼓的形状-等光谱的数学和物理方面。现代物理学评论。 82（3）：2213–2255。 arXiv：1101.1239。 Bibcode：2010RvMP ... 82.2213G。 doi：10.1103 / RevModPhys.82.2213。

卡洛琳·戈登；韦伯，戴维，你听不到鼓的形状，美国科学家，第84卷（1-2月）：46-55岁

戈登角; Webb，D .; Wolpert，S.（1992），＆＃34;通过Riemannian orbifolds的等光谱平面域和表面，发明数学（Inventionses Mathematicae）110（1）：1–22，Bibcode：1992InMat.110 .... 1G，doi：10.1007 / BF01231320

Ivrii，V. Ja。 （1980），“带边界的流形上的Laplace–Beltrami算子的频谱渐近的第二项”，Funktsional。肛门I Prilozhen，14（2）：25-34，doi：10.1007 / BF01086550（俄语）。

Lapidus，Michel L.（1991），＆＃34;有人能听到分形鼓的形状吗？ Weyl-Berry猜想的部分解决方法，《几何分析和计算机图形学》（加利福尼亚州伯克利，1988年），数学。科学Res。研究所纽约大学：Springer，17（17）：119-126，doi：10.1007 / 978-1-4613-9711-3_13，ISBN 978-1-4613-9713-7

Lapidus，Michel L.（1993），B。D. Sleeman中的分形鼓的振动，黎曼假设，分形介质中的波以及Weyl-Berry猜想。 R. J. Jarvis（编），《常微分方程和偏微分方程》，第四卷，过程第十二届国际会议。 Conf。 （Dundee，苏格兰，英国，1992年6月），《 Pitman数学研究笔记》。 289系列，伦敦：Longman and Technical，第126–209页

Lapidus，M. L .； van Frankenhuysen，M.（2000），“分形几何和数论：分形字符串的复杂维数和zeta函数的零”，波士顿：Birkhauser。 （修订并扩大的第二版将于2005年出版。）

Lapidus，Michel L .； Pomerance，Carl（1993），Riemann zeta函数和一维Weyl-Berry猜想，用于分形鼓。伦敦数学。 Soc。，系列3，66（1）：41–69，CiteSeerX 10.1.1.526.854，doi：10.1112 / plms / s3-66.1.41

Lapidus，Michel L .； Pomerance，Carl（1996），“在分形鼓上修改的Weyl-Berry猜想的反例”，Math。程序。剑桥Philos。 Soc。，119（1）：167-178，Bibcode：1996MPCPS.119..167L，doi：10.1017 / S0305004100074053

Milnor，John（1964），在某些流形上的拉普拉斯算子的特征值，美国国家科学院院刊，51（4）：542ff，Bibcode：1964PNAS ... 51..542M，doi：10.1073 / pnas.51.4.542，PMC 300113，PMID 16591156

Sunada，T。（1985），“黎曼覆盖和等光谱流形”，Ann。数学。，2，121（1）：169-186，doi：10.2307 / 1971195，JSTOR 1971195

Zelditch，S.（2000），＆＃34;解析双轴对称平面域的频谱确定，＆＃34;几何和功能分析，10（3）：628–677，arXiv：math / 9901005，doi：10.1007 / PL00001633

Peter Buser，John Horton Conway，Peter Doyle和Klaus-Dieter Semmler的一些平面等光谱域

美国数学协会网站的Ivars Peterson听起来很相似的鼓