经济学中的遍历性问题

ergodic假设是均衡统计力学的关键分析装置。这是假设可观察到的时间平均值和期望值是相同的。在有效的情况下，动态描述通常可以用更简单的概率替换 - 时间基本上消除了模型。有效性的条件是限制性的，甚至更加适用于非平衡系统。经济学通常涉及远离均衡的系统 - 特别是具有生长模型。因此，可能会令人意外地了解经济理论的普遍配方 - 预期的实用理论及其后代 - 造成不分青红皂白的假设。这主要是因为在十七世纪经济学中，这一概念起源于十七世纪的经济学，预测大约200年的崇高性概念，在十九世纪物理学中出现。在这种观点中，我认为，通过仔细解决遍历的问题，许多困扰当前经济形式主义的困难是以自然和经验的可测试的方式解决的。

ergodic理论是一种禁止数学技术分支。幸运的是，出于本讨论的目的，我们几乎不需要技术性。如果其时间平均值等于其期望值，我们将呼叫可观察的ergodic，即如果它满足Birkhoff的等式

$$ \ underbrace {\ mathop {{\ lim}} \ limits_ {t \ to \ int \ intt} \ frac {1} {t} \ mathop {\ int} \ nolimits_0 ^ t {f \ left（{\ omega \ left （t \右）} \右）{\ mathrm {d}} t}}}}}}} _ {{\ mathrm {time}} \; {\ mathrm {平均}} \; {\ mathrm {}} \; f} = \ underbrace {\ mathop {\ int} \ nolimits_ {\ omega} {f \ left（\ omega \ over）p \ left（\ omega \右）{\ mathrm {d}} \ oomega}} _ {{{\ mathrm {期望}} \; {\ mathrm {value}} \; {\ mathrm {}} \; f} $$

这里，F由系统的状态ω确定。在左侧，状态又取决于时间t。在右侧，无线P（ω）为ω分配权重。如果等式（1）保持我们可以避免随时间集成（达到左侧的不同平均时间，而是集成在所有状态，ω（右侧）的空间上。在我们的情况下，P（ω）被给出作为随机过程的分布。在具有瞬态行为的系统中，可能需要将P（ω）定义为T→∞∞∞∞∞限制（ω; t）。

着名的，在均衡统计力学中假设崇拜性，其成功地描述了气体的热力学行为。然而，在更广泛的背景下，许多可观察到不满足等式（1）。事实证明，经济理论令人惊讶地恢复了经济理论，直接询问核心遍历问题：是观察到的时间平均值等于其期望值吗？

在经济学基础的一个关键地方，假设答案总是是的 - 一个有害的错误。为了使经济决定，我经常想知道我的个人财富在不同的情况下的快速增长。这需要确定在某些财富模型中随着时间的推移发生了什么。但是，由于错误地假设讲言，在计算增长之前，财富通常会因其期望值而替换。因为财富不是ergodic，所以出现荒谬的预测。毕竟，期望值有效地平均了无法访问的副本的集合。

此密钥错误与关于人类行为的心理参数进行修补。后果众多，但在几个世纪以来，他们的根本原因在不断增长的形式主义中变得无形。观察到的行为偏离模型预测。与其模型的坚定信念配对，这导致了在经济学的大部分地区的人类非理性的叙述。科学上，这应该得到一些反思：通过宣布研究对象来引起模型。

我偶然发现了大约十年前的这个错误，在伦敦数学实验室和圣菲研究所的合作者，我已经确定了一些来自它的经济学中的一些长期谜题或悖论。如果我们密切关注遍历遍历问题，则自然解决方案出现。因此，我们有理由对经济理论的未来持乐观态度。

这种观点是如下构造的。我将首先绘制主流经济理论的概念基础：折扣预期效用。然后，我将根据解决ergodicity问题，并通过指出映射来建立与主流模型的关系来发展概念上不同的方法。最后，我将报告最近的一个实验室实验，彼此相反的两种方法：他们的预测在哪里有所不同？哪种型号更好地经验？

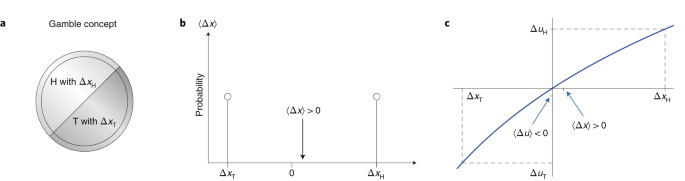
在经济学中，赌博是一个随机变量，δx，代表财富的可能变化x。在离散情况下，这是一组可能的财富变化和相应的概率{（Δxi，p i）}。

例如，赌博可以模拟以下情况：折腾硬币，对于头部，您赢得了50％的当前财富，对于您失去40％的尾部。在数学上，我们可以将此表示为（图1A）：

$$ \ delta {x} = \左\ {{\ begin {array} {\ {\ {x}} {\ {\ rm {h}}} = + 0.5x，\ quad p _ {\ mathrm {h}} = \ frac {1} {2}} \\ {\ delta {x}} = {\ rm {t}}} = {{\ rm {t}}} = - 0.4x，\ quad p _ {\ mathrm {t} } = \ FRAC {1} {2}} \ of {array}} \右。$$

a，事件（这里h和t）与概率p h和p t相关，并且美元财富改变Δxh和δx t.b，赌博的最古老的正式评估计算了预期的财富变化 。 C，预期实用理论通过财富（非线性）实用功能的预期变化评估赌博，，这里U（x）= Ln x为硬币折叠示例。请注意，所有概念都是正式的atemporal。只有大小和概率进入分析。

“赌博”这个词召唤烟雾堆放的赌场和轮盘赌轮的图像。但是，这里的术语是指经济学的普遍概念：正式，我们制造的任何决定都被建模为赌博，是为您的孩子选择幼儿园或决定税务问题。我们从不完全了解后果，而且经济上这通常表达为随机的财富变化。

概率理论的发展是通过赌博问题的动机，早期正式试图在Cardano的精彩（和未发表的罪恶）十六世纪书籍1.实际起点是1654年Fermat和Pascal之间的着名信件交换。他们的通信将期望值作为随机性理论中的关键对象建立。

Pascal和Fermat不是在寻找赌博建议;他们正在解决一个道德问题：即如何以公平的方式评估人们的希望和期望。尽管如此，几年后，以下拇指规则已成为一个完善的行为模型：鉴于两个赌博之间的选择，我们选择了更大的预期财富变化，。该模型预测人们通常会接受等式（2）中的赌博，在这种情况下 = +0.05×（图1B），而替代（不接受）将产生 = 0.5美元。

但是这个模型是否真实？你会接受赌博和风险在掷硬币40％的房子，汽车和救生的折腾吗？

NicolasBernoulli的1713年提出了类似的反对意见3.他提出了一个假设的赌博赌场，其期望值是不同的：ΔX是分布的动力法，其具有不存在的第一时刻。但是，如果我们试图计算期望值，则尚未开发出这种术语，而N.Bernoulli则说明了一些“好奇”。

什么人最终被认为是好奇的是以下内容：如果我们不得不支付费用，f，打这个赌博，应该是什么？预期的财富模式告诉我们，我们将支付任何有限费用，但违反了直觉。尽管δx有一个沉重的尾巴，但非常大的收益的概率仍在消失，而且没有人愿意（假设）以赢得大量的忽略机会。预期财富模型的失败来描述实际的人类行为被称为圣彼得堡悖论，并在许多关于经济学和概率理论的教科书中对待。当我们切换到新的形式主义4时，它是消失的谜题之一。

到1713年，很明显，在不确定性下，有超过预期的财富变化，在不确定的情况下，在1738年，丹尼尔伯努利更新了普遍的理论5：当人们决定是否参加赌博时，他们不会考虑预期的变化财富，x，但预期的财富有用性变化，u（x）。

具体而言，D.Bernoulli妨碍了额外美元的有用性或效用，大致与已经有多少美元的成反比成反比。这导致微分方程D u = 1 / x D x与溶液U（x）= ln x（刚刚发明的微积分）。但他提到广场功能也将有效。通常，单调增加的U（x）反映了更少的财富的偏好，并且凹面U（x）反映了风险的不喜欢。因此，实用程序函数编码特定个人的心理。我们可能会写你勇敢（x）= x，你害怕（x）= ln x。

D. Bernoulli的模型被称为“预期效用理论”。如果效用功能是非线性的，它会产生与预期财富模型不同的偏好，如图1所示。

有趣的是，D.Bernoulli的纸张包含一个错误（参见参考文献4）今天继续困扰着形式主义：在一个地方，他的计算实际上只适用于线性U（x），这将打败介绍u（x）的目的第一个地方。但是，我们不会拍摄D.Bernoulli，而是将他的着作者解释为Laplace 6和von Neumann和Morgenstern 7所做的：我拥有一种特殊的实用程序U I（x），直观计算。如果这是积极的，我们接受赌博，如果它是负面的，我们拒绝它（假设拒绝导致没有财富变化）。

在由等式（2）所描述的硬币折叠示例中，D.Bernoulli的对数实用程序的预期变化是≈〜0.05。因此，你害怕的心理学的人不会接受赌博。

实用理论考虑一个静态概率空间，没有明确的时间。例如，D.Bernoulli和他的追随者没有讨论公用事业的变化率，而只是改变的大小。

时间是单独处理的，即通过称为折扣的过程。最初，折扣为未来收到的付款分配了本值。它通常用无仲裁论点证明：如果可以在T +ΔT中稍后收到的时间t，则稍后收到的付款，如果它可以用于持续时间δt，则值得超过稍后收到的付款。

通过参考圣经感兴趣（例如，申命记23:19），时间折扣的实践比公用事业的概念更早。今天，这两个概念共存但没有多么清晰，关于他们各自的域名：基于无套利的论据，一个人会折扣现金，但自1937年以来，它一直是折扣公用事业 - 甚至没有现金的效用，而是现金甚至是现金的效用更多的一般资源8。

No-arbitrage论点与可用的投资选择贴现。但是，在一般性的雄心勃勃的尝试中，现在折扣通常就是另一种主观函数的措辞（ΔT）：我们中的一些人不耐烦，并且具有快速腐烂（ΔT）强烈折扣;其他人更耐心。据称（ΔT）的功能形式是我们心理学的另一部分 - 它可以是双曲线或指数的，或者其他任何符合数据9。

首先，我们考虑没有不确定性的财务决策，这与原始折扣概念非常相似。在第二步中，我们通过引入噪音来推广。放置考虑时间和遍历性中心阶段，我们将在明确的解释中到达折扣和实用理论，而不吸引主观心理或确实是其他形式的个性化。

没有不确定性的赌博只是付款。一个琐碎的模型将是：我们接受正面的付款并拒绝消极的付款。但如果我们必须在不同时间选择两次付款或付款流之间，那么怎么办？

在这种情况下，一次考虑必须是某种形式的增长率。例如，我可以选择提供每年12,000美元的作业，另一个提供每月2,000美元的工作。让我们说工作在所有其他方面都是相同的：我会选择每月支付2,000美元的人 - 不是因为2,000美元是更高的付款（它不是），而是因为支付对应于更高（添加剂）的增长率我的财富。我会最大化

或者，我可以在两个储蓄账户之间进行选择。一个人每年支付4％，另一个每月1％ - 再次，这是我将优化的增长率：在这种情况下是指数增长率

由于ΔT划分了大量非线性函数的差异，因此现在进入具有明确的含义，但在潜在的相当复杂的方式 - 在等式（3）中以等式（3）或以等式指数（4）指数。

投资的添加剂收益和乘法回报是改变我们财富的两个最常见的过程，但我们可以考虑其增长率将具有不同功能形式的其他增长过程。例如，体重与时间的生物学，体重与时间的生长曲线的生长速率具有不同的功能形式10.对于任意生长过程x（t），一般生长速率是

其中V（x）是选择的单调增加功能，使得G不会及时改变。添加剂和乘法生长对应于V a（x）= x和v e（x）= ln x。概括，v（x）是单位速率下的过程x（t）的倒数，表示

对于财务流程，拟合更一般的功能通常会导致线性和对数之间的插值，也可能在方函数中或类似的小调整。

现实生活通常具有一定程度的不确定性。我们让模型通过引入噪音来反映这一点。但怎么样？

以一致的方式扰乱该过程，我们提醒自己，在没有噪声的情况下，对过程的常数是增长率。如果我们扰乱了具有恒定幅度噪声的，则扰动的比例将是在V空间中独立的时间，并且在这种感觉适应动态的情况下。通过以差异形式写入等式（5），通过其（常数）值，γ表示，重新排列和添加噪声（这里由带幅度σ表示的噪声来替换函数g

通过集成等式（7）并求解X来发现该过程本身。对于我们的两个关键示例，这会产生布朗运动（用V a = x）和几何布朗运动（用v e = ln x）。

这些过程的增长率不再是不变的，因为它们是嘈杂的。但缺乏持续态度是由于噪音之外的任何东西。使用等式（1）中引入的命名法，相关的生长率是各自过程的ergodic可观察。通过设计，他们的（时间或合奏）平均线路告诉我们随着时间的推移往往发生了什么。

这不是财富本身的情况，它将预期的财富模型暴露为身体幼稚。预期的财富变化根本无法反映随着时间的推移发生的事情（除非财富动态是添加剂;图2）。初步矫正预期实用理论 - 忽略了物理问题，跳到了心理争论，这很难限制和经常是通函。

示例赌博在等式（2）中给出。期望值，（蓝线）是无限集合的平均值，但它不会反映随着时间的推移发生的事情。用于过程的ergodic生长速率（红线的斜率）告诉我们典型的单个轨迹会发生什么。显示了150个轨迹，每个轨迹都包含1000次重复。

增长速率优化现在有时被称为“ergodicity经济学”。这并不意味着假设ergodicity - 相反：它是指通过明确询问某些东西是否是ergodic来做经济学，这通常不是这种情况。正如我们所看到的，Ergodicity经济学是一个透视，它由构建非ergodic（生长）过程构建ergodic可观察结果。

预期的效用理论和ergodicity经济学都会引入财富的非线性变换，以及两个框架中出现的方程可以非常相似。更确切地说，映射是：给定过程的适当增长率与特定效用函数的变化率正式相同

由于遍历性，这种增长率的时间平均值与特定预期效用功能的变化率相同。

尽管映射，但概念上，这两种方法不能更不同，遍历经济学仍然更接近物理现实。

预期的实用理论是映射的松散端，因为它提供的唯一限制函数它提供了对心理的引用。虽然有些人认为这是一种确保普遍性的一种方式，但我的第二批评更严重，而且我无法解决它：在最大化期望值 - 在赌博预期实用理论的所有可能结果中的集合平均值隐含地假设个人可以在平行宇宙（合奏的其他成员）中有效地与自己的副本互动。非ergodic观察的期望值物理上对应于许多实体之间的汇集和共享。这可能反映出特殊设计的大集体中发生的事情，但它不会反映个体决策者的情况。

预期的实用理论计算在多个人间平均了对我的心理学的松散指定模型发生了什么。但我没有生活在多个人身上，更不用说收获了我多数克隆的行为的平均心理后果。

相比之下，ergodicity经济学计算在时间流逝的情况下，在没有吸引无形心理学或多层的情况下，在没有吸引力的情况下，可以在我的身体财富发生什么。我们都通过时间才能实现，并遭受我们年轻人行为的身体后果（和心理后果）。

凭借ergodicity经济学，某些人系统地比其他人更加谨慎的心理洞察力达到了物理解释。也许人们没有那么不同，但他们的情况是。最大化添加剂过程中增长的人似乎是勇敢的：v a =你勇敢，而同一个人做同样的事情，但对于乘法过程似乎害怕：v e =你害怕。还要注意这些陈述的比例依赖性：相同的δx（以美元计）对应于穷人的大型对数财富变化以及富人的小对数变化 - 后者是可直观的，而富人看起来勇敢。

它也造成历史意义：在概率理论的早期存在的初步信念，即在期望值方面应该表达的事情。为此，在个人制定财务决策的人的背景下进行任何意义，必须创建一个遍历可观察的可观察。预期的效用理论 - 在不知不觉中，因为遍布遍历尚未发明 - 做到了。但由于缺乏概念清晰度，整个经济领域都陷入了太多EMP的方向

......