Amdahl的法律

跳转到导航跳转以搜索计算机架构，amdahl＆＃39; s法律（或amdahl＆＃39; s论点[1]）是一个公式，它给出了可以是固定工作负载执行任务的延迟的理论加速预期的资源得到改善的系统。它以电脑科学家基因Amdahl命名，并于1967年在AFIPS Spring Compon Computer Conference展出。

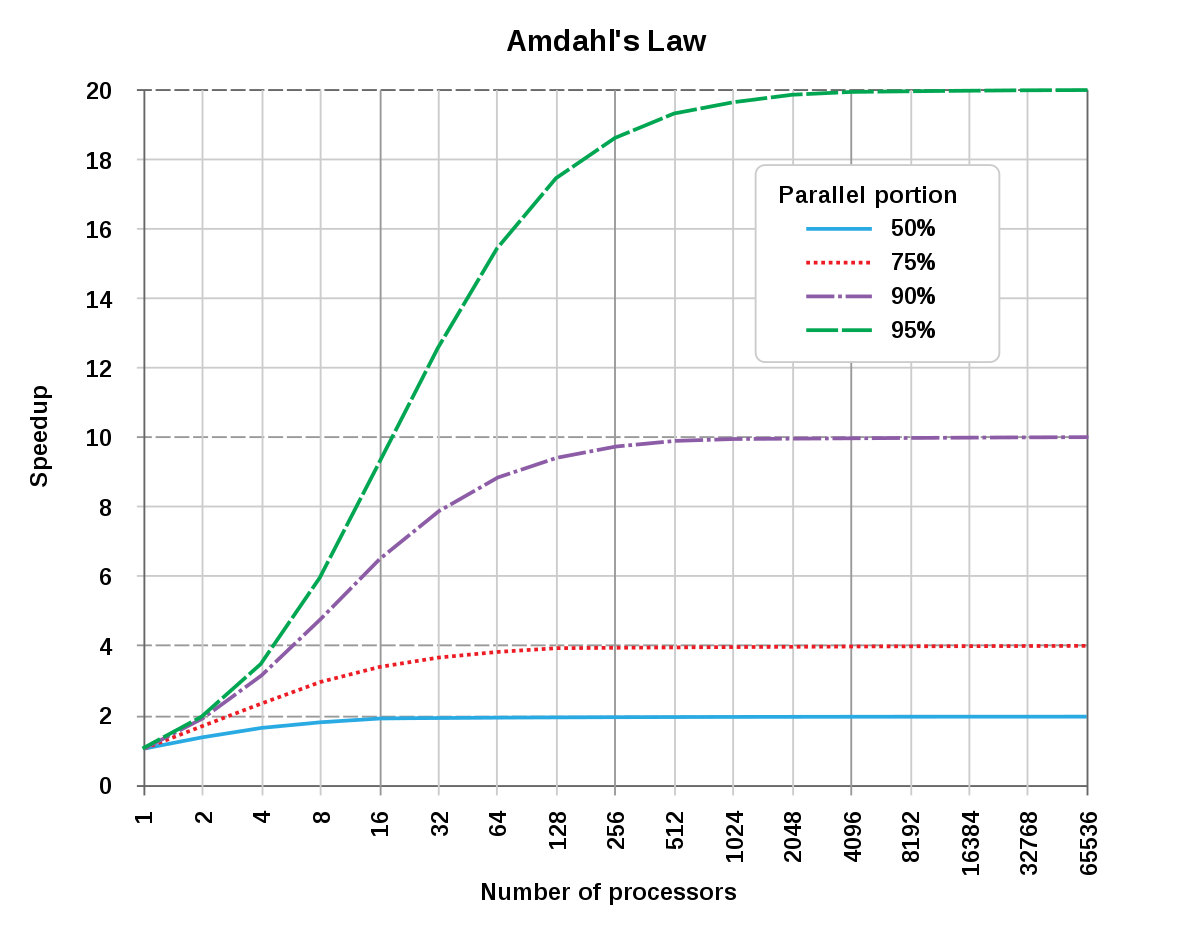
Amdahl＆＃39; S法通常用于并行计算，以预测使用多个处理器时的理论加速。例如，如果程序需要20小时才能使用单个线程完成，但程序的一小时部分不能并行化，因此只有剩余的19小时（P = 0.95）的执行时间可以并行化，然后无论有多少个线程被致力于该程序的并行执行，最小执行时间不能小于一小时。因此，理论加速度限制为单线程性能的最多20倍，（1 1-p = 20）{\ displaystyle \ left（{\ dfrac {1} {1-p}} = 20 \右）}。

s延迟（s）= 1（1 - p）+ ps {\ displaystyle s _ {\ text {latency}}（s）= {\ frac {1} {（1-p）+ {\ frac {p} {s }}}}}}

s是从改进的系统资源中获益的任务的重播;

P是从最初占用的改进资源受益的部分的执行时间比例。

{S延迟（s）≤11 - p lim s→∞s延迟= 1 1 - p。 {\ displaystyle {\ begin {is} s _ {\ text {latency}}（s）\ leq {\ dfrac {1} {1-p}} \\ [8pt] \ lin \ linits _ {s \ to \ infty } s _ {\ text {latency}}（s）= {\ dfrac {1} {1-p}}。\结束{is}}}

表明，整个任务的执行的理论加速随着系统资源的提高而增加，而不管改进的幅度如何，理论加速度总是受到无法从改进中受益的任务的部分限制。

Amdahl＆＃39; S法仅适用于解决问题规模的情况。在实践中，随着更多计算资源可用，它们往往会用于更大的问题（较大的数据集），并且在并行部分中花费的时间通常会比固有的串行工作更快地增长。在这种情况下，Gustafson＆＃39;法律给出了对平行性能的悲观和更现实的评估。 [3]

与初始类似系统相比，资源改进的系统执行的任务可以分为两部分：

一部分，不会从系统资源的改进中受益;

一个例子是从磁盘处理文件的计算机程序。该程序的一部分可以扫描磁盘的目录，并在内存内部创建文件列表。之后，程序的另一部分将每个文件传递给单独的线程以进行处理。扫描目录并创建文件列表的部分不能在并行计算机上加速，但是处理文件可以的部分。

在系统资源的改进之前整个任务的执行时间表示为t {\ displaystyle t}。它包括不会受益于资源的改进和将受益于它的执行时间的部分的执行时间。将从资源的改进中受益的任务的执行时间的分数由p {\ displaystyle p}表示。因此，一个关于不会受益于它的部分的一个是1 - p {\ displaystyle 1-p}。然后：

它是在改进资源后，在改进资源后，执行这些部分的利益，从而改善了因子S {\ displaystyle s}。因此，不会受益于它的部分的执行时间仍然是相同的，而其中的部分则成为：

在改进资源后整个任务的理论执行时间t（s）{\ displaystyle t（s）}

t（s）=（1 - p）t + p s t。 {\ displaystyle t（s）=（1-p）t + {\ frac {p} {s}} t。}

Amdahl＆＃39; S法律提供了在固定工作负载W {\ DisplayStyle W}处执行整个​​任务的延迟的理论加速，这是产生的

S延迟（s）= t w t（s）w = t t（s）= 1 1-p + p s。 {\ displaystyle s _ {\ text {latency}}（s）= {\ frac {tw} {t（s）w}} = {\ frac {t} {t（s）} = {\ frac {1} {1-p + {\ frac {p} {s}}}}。}。}

如果执行时间的30％可能是加速的主题，则P将为0.3;如果改进使受影响的部分快速，S将是2.AMDAHL＆＃39;法律规定，申请改进的总体加速将是：

S Latency = 1 1 - P + P S = 1 1 - 0.3 + 0.3 2 = 1.18。 {\ displaystyle s _ {\ text {latency}} = {\ frac {1} {1-p + {\ frac {p} {s}}} = {\ frac {1} {1-0.3 + {\ frac { 0.3} {2}}}}}}} = 1.18。}

例如，假设我们被赋予串行任务，该任务被分成四个连续部分，其执行时间的百分比分别为p1 = 0.11，p2 = 0.18，p3 = 0.23和p4 = 0.48。然后我们被告知第一个部分没有加速，所以S1 = 1，而第二部分被加速5次，所以S2 = 5，第3部分被加速20次，所以S3 = 20，以及第4个部分加快1.6倍，所以S4 = 1.6。通过使用Amdahl＆＃39; SAW，整体加速是

S延迟= 1 p 1 s 1 + P 2 s 2 + P 3 S 3 + P 4 S 4 = 1 0.111 + 0.18 5 + 0.23 20 + 0.48 1.6 = 2.19。 {\ displaystyle s _ {\ text {latency}} = {\ frac {1} {{\ frac {p1} {s1} + {\ frac {p2} {s2} + {\ frac {p3} {s3} } + {\ frac {p4} {s4}}}} = {\ frac {011} {{\ frac {0.11} {1}} + {\ frac {0.18} {5}} + {\ frac {0.23} {20}} + {\ FRAC {0.48} {1.6}}}} = 2.19。}

请注意，当第4部分（执行时间的48％）加速1.6倍时，分别在2ND和第3零件上加速5次和第3零件的加速时间和第3零件的加速。 例如，在A和B中的两个部分A和B有一个序列程序，其中T a = 3 s和t b = 1 s， 如果B部分更快地运行5倍，则S = 5且P = T B /（T A + T B）= 0.25 S Latency = 1 1 - 0.25 + 0.25 5 = 1.25; {\ displaystyle s _ {\ text {latency}} = {\ frac {1} {1-0.25 + {\ frac {0.25} {5}}} = 1.25;}} = 1.25; 如果A部分是更快地运行2倍，那就是s = 2并且p = t a /（t a + t b）= 0.75 S Latency = 1 1 - 0.75 + 0.75 2 = 1.60。 {\ displaystyle s _ {\ text {latency}} = {\ frac {1} {1-0.75 + {\ frac {0.75} {2}}} = 1.60。} 因此，使部件A更快地运行2倍，比制作B部分更快地运行5倍。 可以计算速度的提高百分比

百分比改进= 100（1 - 1次）。 {\ displaystyle {\ text {百分比改进}} = 100 \ left（1 - {\ frac {1} {s _ {\ text {latency}}}}}}

改进部分A倍率2将以1.60重量乘数将整体程序速度提高，这使其比原始计算快37.5％。

然而，改进B部分5倍，这可能需要更多的努力，只能达到1.25的整体加速因子，这使得20％更快。

如果不行化部分由O {\ DISPLAYSTYLE O}的因子优化，那么

T（o，s）=（1 - p）t o + p s t。 {\ displaystyle t（o，s）=（1-p）{\ frac {t} {o}} + {\ frac {p} {s}} t。}

S延迟（o，s）= t（o）t（o，s）=（1 - p）1 o + p 1 - p o + p s。 {\ displaystyle s _ {\ text {latency}}（o，s）= {\ frac {t（o）} {t（o，s）}} = {\ frac {（1-p）{\ frac {1 }。

当s = 1 {\ displaystyle s = 1}时，我们有s等待时间（o，s）= 1 {\ displaystyle s _ {\ text {latency}}（o，s）= 1}，这意味着加速是令人尊重的在优化不行化部分后的执行时间。

S等待时间（O，∞）= T（O）T（O）T（O，S）=（1 - P）1 O + P 1 - P o + P S = 1 + P 1 - P o。 {\ displaystyle s _ {\ text {latency}}（o，\ idty）= {\ frac {t（o）} {t（o，s）}} = {\ frac {（1-p）{\ frac { 1} {o}} {{\ frac {1-p} {o}} + {\ frac {p} {s}}}} = 1 + {\ frac {p} {1-p } o。}

如果1 - p = 0.4 {\ displaystyle 1-p = 0.4}，则o = 2 {\ displaystyle o = 2}，s = 5 {\ displaystyle s = 5}，然后：

S等待时间（O，S）= T（O）T（O，S）= 0.4 1 2 + 0.6 0.4 2 + 0.6 5 = 2.5。 {\ displaystyle s _ {\ text {latency}}（o，s）= {\ frac {t（o）} {t（o，s）}} {t（o，s）}} = {\ frac {{0.4} {\ frac {1} { 2}} + 0.6} {{\ frac {0.4} {2}} + {\ FRAC {0.6} {5}}} = 2.5。}

接下来，我们考虑一种不正分化部分减少的情况，减少了{\ displaystyle o＆＃39;}，并且相应地增加了并行部分。然后

T'（O'，S）= 1 - P o'T +（1 - 1 - P o'）t s。 {\ DisplayStyle T＆＃39;（O＆＃39;，s）= {\ frac {1-p} {o＆＃39;} t + \ left（1 - {\ frac {1-p} {o＆＃39; }} \右）{\ frac {t} {s}}。}

S延迟'（O'，S）= T'（O'）T'（O'，S）= 1 1 - P o'+（1 - 1 - P o'）1 s。 {\ displaystyle s＆＃39; _ {\ text {latency}}（o＆＃39;，s）= {\ frac {t＆＃39;（o＆＃39;）} {t＆＃39;（o＆＃39;， s）}}}}}} = {\ frac {1-p} {o＆＃39;}} + \ left（1 - {\ frac {1-p} {o＆＃39;}} \ ）{\ FRAC {1} {s}}}}}。}

上面的推导与Jakob Jenkov＆＃39;分析执行时间与加速权衡的分析。 [4]

Amdahl＆＃39; S法常常与回报递减规律混淆，而只有一个申请Amdahl＆＃39;法律的特殊情况证明了回报递减的法律。如果一个人最佳地（在实现的加速度方面）将改进的改进，那么一个人会看到单调地减少改善的改进。然而，如果一个人在改善子最优分量并继续前进以改善更优化的组件之后，则可以看到返回的增加。请注意，通过＆＃34的顺序改进系统通常是合理的，以改善一个＆＃34;非最佳＆＃34;从这个意义上讲，鉴于一些改进更加困难或需要比其他更大的开发时间。

Amdahl＆＃39;法律确实代表了递减的定律，如果考虑到一台机器，如果一个人运行一个固定尺寸的计算，那么将更多的处理器将所有可用的处理器用于它们的容量来实现，如果运行了哪种返回，则表示返回的定律。添加到系统的每个新处理器都会添加比前一个更少的功耗。每次加倍处理器的数量时，加速比率会减少，因为总吞吐量朝向1 /（1 - P）的极限。

此分析忽略了其他潜在的瓶颈，如内存带宽和I / O带宽。如果这些资源不与处理器的数量扩展，则仅添加处理器提供甚至返回返回。

AMDAHL＆＃39; S法的含义是加速具有串行和并联部分的真实应用，需要异构计算技术。例如，CPU-GPU异构处理器可以提供比仅CPU或GPU处理器更高的性能和能量效率。 [6]

^ Rodgers，David P.（1985年6月）。 ＆＃34;多处理器系统设计的改进＆＃34; ACM SIGIGINCH计算机建筑新闻。纽约，纽约，美国：ACM。 13（3）：225-231 [p。 226]。 DOI：10.1145 / 327070.327215。 ISBN 0-8186-0634-7。 ISSN 0163-5964。

^ Bryant，Randal E .; David，O＆＃39; Hallaron（2016），计算机系统：程序员＆＃39;透视（3 ED），Pearson教育，p。 58，ISBN 978-1-488-67207-1

^ Miccool，Michael;杰克斯，詹姆斯; Robison，Arch（2013）。结构化并行编程：有效计算模式。 elewsvier。 p。 61. ISBN 978-0-12-415993-8。

^ Hill，Mark D .; Marty，Michael R.（2008）。 ＆＃34; amdahl＆＃39; Matheryor Era＆＃34的法律;电脑。 41（7）：33-38。 DOI：10.1109 / MC.2008.209。

^ Mittal，Sparsh; Vetter，Jeffrey S.（2015）。 ＆＃34; CPU-GPU异构计算技术＆＃34; ACM计算调查。 47（4）。 69. DOI：10.1145 / 2788396。

Amdahl，Gene M.（1967）。 ＆＃34;单个处理器方法的有效性，实现大规模计算能力＆＃34; （PDF）。 AFSIPS会议课程（30）：483-485。 DOI：10.1145 / 1465482.1465560。

＆＃34;并行编程：当Amdahl＆＃39; S法中不适用？＆＃34; 2011-06-25。从原版存档2013-04-14。

基因M. Amdahl（1989），口头历史访谈Gene M. Amdahl，Charles Babbiggab Institute，明尼苏达大学，HDL：11299/104341。 Amdahl讨论了他在威斯康星大学的研究生工作和他的WISC设计。讨论他在IBM的几台计算机设计中的作用，包括拉伸，IBM 701和IBM 704.他与Nathaniel Rochester和IBM的工作讨论了设计过程的管理。提到与Ramo-Wooldridge，Aeronutronic和计算机科学公司一起工作

英特尔酷睿i7涡轮增压的评估，由James Charles，Preet Jassi，Abanth Narayan S，Abbas Sadat和Alexandra Fedorova（2009）

计算并行计划加速程序作为线程数量的函数，由乔治波波夫，瓦莱·兆头和尼科斯·米拉基（2010年1月）