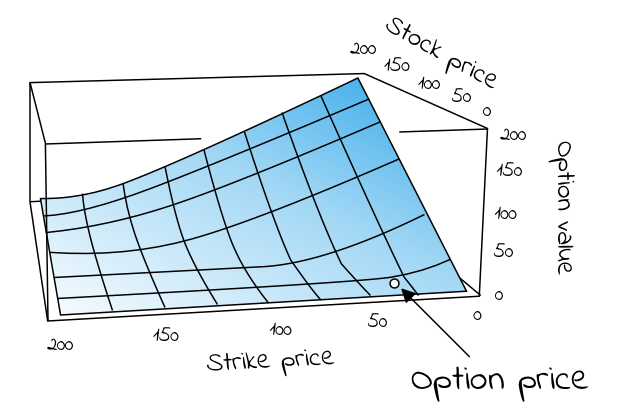
用TSLA示例解释了Black-Scholes公式

Black-Scholes模型是模拟含有衍生金融工具的金融市场动态的数学模型。自1973年引进并在20世纪70年代和80年代的改进以来，该模型已成为估算股票期权价格的脱桃标准。模型背后的关键观点是通过以正确的方式购买和销售潜在的资产（如股票）对冲投资组合中的选择，并因此消除风险。该方法后来在金融中被称为“不断修订的套期套期”，并被世界上最重要的投资银行和对冲基金所采用。

本文的目标是解释Black-Scholes等式的数学基础，潜在的假设和含义。

Black-Scholes模型是模拟含有衍生金融工具的金融市场动态的数学模型，如选项，期货，前进和换档。该模型的关键属性在于它表明，无论潜在安全的风险及其预期回报都有独特的价格。该模型基于部分微分方程（PDE），所谓的Black-Scholes方程，可以从中推断为Black-Scholes公式，这给出了欧洲股票期权价格的正确价格的理论估计。

原始的Black-Scholes模型基于核心假设，即市场由至少一个风险资产（如股票）和一个（基本上）无风险资产组成，例如金钱市场基金，现金或政府债券。此外，它还假设两个资产的三个属性，以及四个市场本身：

关于市场资产的假设是：1。无风险资产的回报率是恒定的（因此有效地表现为利率）; 2.根据几何布朗运动，假设风险资产价格的瞬时日志返回的行为作为无限漂移和波动的无限随机行走。 3.风险资产不支付股息。

关于市场本身的假设是：1。没有套利（无风险的利润）机会; 2.有可能以与无风险资产的利率相同的税率借用并贷款; 3.可以购买和销售任何金额（包括卖空）; 4.市场上没有交易成本（即购买或销售证券或衍生工具的佣金）。

在原始模型的后续扩展中，这些假设已被修订，以调整无风险资产的动态利率（Merton，1976），购买和销售的交易成本（Ingersoll，1976）和风险资产的股息支付（ Whaley，1981）。在本文中，假设我们正在使用原始模型，除非另有说明。

Black-Scholes方程是根据Black-Scholes（有时Black-Scholes-Merton）模型运行的金融市场中欧洲股票期权价格演变的部分微分方程（PDE）。等式是：

其中V是选项的价格（作为两个变量的函数：股价s和时间t），r是无风险的利率（思考利率类似于您将从资金市场基金中收到的利率，德国政府债务或类似“安全”债务证券“和Σ是基础安全的日志返回的波动（出于本条的目的，我们正在考虑库存）。基于John C. Hull的“期权，期货和其他衍生品”（1989年），在维基百科提供了方程的整洁推导。

然后，左侧代表了选项v的值/价格的变化，由于时间t增加了+期权值相对于库存价格的凸起。右手侧代表了从期间的长位置的无风险回报，以及由库存的∂v/∂s股份组成的短位置。就希腊人而言：

Black和Scholes（1973）的关键观察是，在任何无限时间间隔的右侧组合的股票和选项的无风险回报可以表达为θ（θ）和术语的总和伽玛（γ）。观察有时被称为“风险中性论证”。这是因为θ（θ）的值通常是否定的（因为随着时间的时间移动更接近到期时，选项的值减小），并且伽马（γ）的值通常是正的（反映了组合接收的增益接收到选项） 。总而言之，θ的损失和从伽马抵消的收益彼此偏移，导致无风险率返回。

鉴于以下边界条件（EQ.4和5），Black-Scholes公式是Black-Scholes PDE的解决方案。它计算欧洲投入和呼叫选项的价格。也就是说，它根据未来预定日期，计算权利（但不是义务）的合同价格（但不是义务），以预先确定的价格在预定的价格上购买或销售一些底层资产。在到期/到期（t），分别给出了这种欧洲呼叫（c）和put（p）选项的价值：

黑色和斯科尔斯展示了对Black-Scholes方程（EQ.1.上文）的分析解决方案的功能形式，具有方程元给出的边界条件。 4和5，对于欧洲通话选项是：

该公式为非股息支付股票提供欧洲呼叫选项的价值/价格。进入公式的因素是s =安全性，t =到期日，t =当前日期，x =行使价格，r =无风险利率和σ=波动性（标准资产的标准偏差）。函数n（·）表示正常（高斯）分布的累积分布函数，并且可以被认为是正常分布的概率为“随机变量较小或等于其输入（即d₁和d 2”。作为概率，换句话说，值n（·）将始终在0≤n（·）≤1之间。输入D 1和D 2由：

非常非正式地，Black-Scholes公式给出的两项术语可能被认为是“股票的当前价格被您将运送您的选择购买库存减去”折扣锻炼价格概率加权的选项，您将锻炼的概率“，或简单地”您将要递减“您要付费的东西”（Khan，2013）。

对于欧洲的选项（权利合同但不是义务，以预先确定的价格在未来的预先确定的价格上以预先确定的日期出售一些劣等的资产）等价职能表格是：

为了计算欧洲呼叫选项的价格应该是什么，我们知道我们需要上面的等式6所需的五个值。它们是：1。目前库存价格，2.呼叫选项的行使价格（x），3.到期时间（t - t），4.无风险利率（r ）和5.股票的波动性，由历史记录返回的标准偏差给出（σ）。

估算Tesla（TSLA）的呼叫选项的值，我们需要的前四个值是可以轻松获得的。假设我们对Tesla股票（$ TSLA）的通话选项感兴趣，2019年的Q3收益的日期成熟，价格高于股票目前交易的价格。在今天（2019年7月13日）的雅虎金融上查看Tesla的纳斯达克上市（$ TSLA），我们发现S = 245美元的股票价格。将当前价格乘以1.2给我们的行使价格高于股票目前交易的20％，x = 294美元。谷歌，我们发现其Q3盈利呼吁的日子是10月22日，给我们一个时间到期/ 10月22日到期 - 7月13日= 101天。作为无风险利率仪器的代理，我们将使用10年政府债券（$ USGG10YR），目前支付2.12％。所以，我们发现S = 245，x = 294，T-T = 101和r = 0.0212。唯一缺失的价值是股票波动率（σ）的估计。

我们可以通过在不同成熟/到期日（t）和运动/罢工价格（x）中计算同一股票的其他选择价格，估计任何股票价格，或甚至更简单。根据Black-Scholes模型设置。得到的值σ是0到1的数字，代表市场对库存的隐含波动。对于TESLA，在撰写本文时，围绕同一到期/到期日期间的4-5个不同期权价格的平均值平均为约0.38。输入到上面的等式6，我们发现我们感兴趣的呼叫选项应该是7美元的价格。

虽然了解选项发行人如何获得他们的呼叫价格以及将选项的价格到达，但投资者难以“不同意”的价格，本身，这么难以将这些知识转化为可行的投资论文。

然而，如果我们将选项（c或p）的价格视为已知数量/独立变量（通过查看不同的成熟日期和不同练习和不同的锻炼）将选项（c或p）的价格视为对黑人学生公式，则可以获得大量的milage价格x）。这是因为，如果我们这样做，Black-Scholes功能方程就成为一种帮助我们了解市场如何估计股票的波动，也称为选项的隐含波动性。这是我们可以不同意的信息和贸易。

假设情景如果我们例如在过去的三个月内查看Tesla股票的图表（图2），我们看到了一个相当（因为缺乏一个更好的单词）挥发性旅行从徘徊在三个月前约280美元，到了一个低每月180美元，即可在备份到245美元的路上。鉴于我们之前观察到的波动率（280-180美元= 100美元，100/280美元，100/280 = 0.36，VS 0.38），这是有道理的。然而，如果我们认为过去三个月的波动是冰山中的波动，因此由于即将延续的短销售增加，进入Tesla的更具波动的时期。

让＆＃39;据说我们不同意一个关于股票暗示波动性的选项发行人，在过去三个月内的表现。我们认为骑行将获得Rockier。多少？让＆＃39; S这样说，而不是40％，我们认为接下来的三个月看起来更像60％。输入功能Black-Scholes公式以及S，X，R和T - T的相同值，我们获得了近两次选项发行人想要的价格，在C（S，T）= 14.32美元。我们可以进行交易。例如，我们可以在销售利润之前等待今天购买呼叫选项，并等待波动增加或增加股票的价值。

由于美国的选择可以在到期前的任何日期（所谓的“连续时间线仪器”），因此它们更难以处理欧洲选项（“时间仪器”）。主要是，由于最佳运动策略将影响选项的价值，因此在解决黑人级微分方程时需要考虑这一点。根据Black-Scholes方程，没有已知的“封闭式”解决方案。但是，有些特殊情况：

对于不支付股息（或其他支出）的潜在资产的美国呼叫选项，美国的呼叫期权价格与欧洲呼叫选项相同。这是因为在这种情况下最佳运动策略是不锻炼选项。

对于在其寿命中支付一个已知股息的潜在资产的美国呼叫选择，早期行使选项可能是最佳的。在这种情况下，根据所谓的Roll-Geske-Whaley方法给出封闭式的解决方案，1981）：

首先，通过调查是否满足以下不等式来检查是否最佳地锻炼选项：

对于S =股票价格，X =练习价格，D₁=股息支付，T =当前日期，T₁=股息付款日期，T =期权到期日期。

如果不平等没有满足，早期锻炼它就不是最佳的。如果C（·）是欧洲呼叫选项上的常规Black-Scholes公式（eq x），那么美国呼叫选项的值由股票价格相同的等式的版本给出（ s）折扣：

如果履行不等式，早期运动是最佳的，美国呼叫选项的价值是由以下方面的糟糕，乱七类交易所给出的（我试图通过每个术语分解它来使它更可读）：

在之前的=股票价格之前，t =期权到期日，x =行使价格和r =无风险利率，σ=波动率（股票历史回报的标准偏差），和d₁是股息支付。此外，ρ是：

它应该不言而喻，黑人模型恰恰认为，鉴于上述假设以及我们自己的无风险利率（R）的数值估计的固有局限性以及我们自己的无风险利率（R）和的固有局限性的理论模型未来波动率（σ）。这里应该突出显示，并非所有（尤其是原始模型）的所有假设实际上都经验有效。例如，出现了显着的限制：

这些应在任何和所有投资策略中占，例如通过对扣押的拒绝进行对冲，在多种交流中进行交易，分别对冲疏忽和伽马套期保值。

简要介绍，它是1973年的费舍黑人和迈尔斯·斯科勒斯州，他们认为，根据某些规则动态修改了投资组合，从而消除了基础安全的预期回报（Black＆amp; Scholes，1973）。他们的型号由Bachelier，Samuelson和其他人建立在以前建立的作品。 Robert C. Merton是第一个发布对模型的理解的论文，并创造了“Black-Scholes选项定价模型”一词。斯科尔斯和默顿被授予1997年诺贝尔经济科学纪念奖，以发现从其底层证券的风险中解散股票期权的方法。随着菲舍尔的黑人于1995年通过，他将没有资格获得奖项，但被纳入诺贝尔学院的贡献者被承认。