证明50岁的排序网络最佳：第1部分

去年12月，我完成了一篇论文，其中我在1969年证明了Shapiro和Green发现的11和12通道排序网络的最佳性，这是D. E.Knuth的“计算机编程艺术”Vol。 3 [8]。虽然他们被猜测很长一段时间是最佳的，但证明这一直是一个开放的问题。

在这篇文章中，我将介绍问题并提供一些上下文。在未来的帖子中，我将描述我的结果以及我如何到达那里。如果您对所有证明和技术详细信息感兴趣，您可以阅读纸质并立即查看随附的源代码和正式证明。

排序列表必须是计算机科学中最受研究的最多的问题之一。大多数时间都是通过比较排序来完成的，这些排序仅是通过将它们中的两个人进行比较来获取其相对顺序来检查项目的算法。这是一种非常一般的方法，因为它不使用除具有线性顺序之外的物品表示或任何特定属性。 QuickSort，Merge Sort和HeaP排序属于此类，而RADIX排序或计数排序的方法则不会。

在所有这些比较中，但是，比较项目中的信息较小，影响之后执行的步骤。当然，在某种程度上，必须使用该信息，但我们可以将其限制在绝对最小值。我们仅使用比较交换操作来执行此操作。比较交换是对两个项目的比较，然后选择两个项目，然后选择它们以后处于已知订单。或者，您可以将其视为替换一对值，其最小和最大值以指定的顺序。仅使用比较交换操作的排序算法而不查看哪个项目的较小值被称为数据忽略（比较）排序算法。

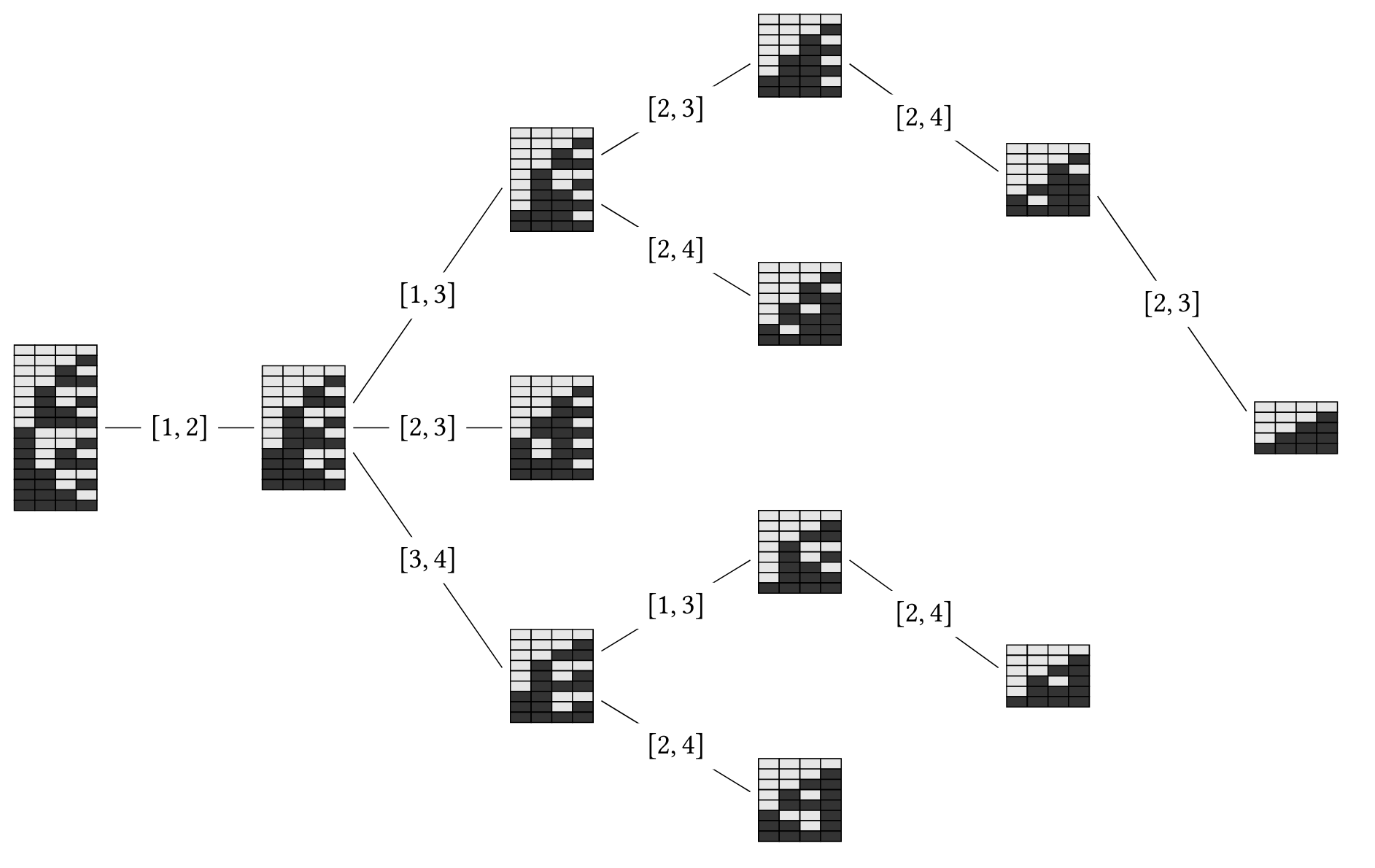
如果我们进一步降低任何大小的排序列表的要求，而是修复输入长度，我们获得称为排序网络的东西。通过它执行的比较交换操作列表完全指定排序网络。在排序网络的上下文中，位置1，...，n 1，\ ldots，n 1，...，n n称为信道，并且比较交换操作也称为比较器。为了指定比较器，我们在方括号（例如[1,3] [1,3] [1,3]）中写入一对通道，其中第一信道接收较小的值和第二信道更大的值。要指定排序网络，我们从左到右写入执行的操作（例如[1,3] [1,2] [2,3] [1,3] [1,2] [2,3] [1 ，3] [1,2] [2,3]）。

这里，水平线对应于通道。从左到右的每个比较器都被绘制为垂直线，从比较器的第一个通道开始并在比较器的第二通道中结束。现在这是模糊的，因为比较器不是对称的 - 一个通道接收较小的值，并且通过惯例的较大的较大的通道接收较小的值。如果我们希望与其他方式取向比较器，我们将它们绘制为指向接收较大值的频道的箭头。此外，我们还可以使用无条件交换来重新排序通道，使用圆括号编写，如下所示：

事实证明，我们只需要默认的比较器方向，不需要无条件交换。使用下面的重写规则，由R. W.Floyd和D.E.Charuth [5]给出，我们可以始终重新排列网络以摆脱无主管的比较器和无条件交换。因此，我们将分类网络的大小定义为其比较器的数量，并且不计算任何无条件交换。

然而，随着我们认为适合的额外自由，通过无条件交换，可以帮助我们分析排序网络时提供帮助。

在我们深入进入分析和构建分类网络之前，我想提及它们是有用的。

排序网络的大优点是它们可以在没有任何数据相关的控制流程的情况下实现。通常可以通过使用条件移动或一些位双重模拟那些来实现单个比较器而无需分支。使用这种比较器，单个排序网络只是一个无线分支的指令序列。像这样的程序有时也称为直线程序。这是一个对现代CPU已经有用，不可预测的分支机构具有沉重的绩效罚款。但它还允许使用SIMD指令同时对多个序列进行排序，其中每个SIMD通道用于对一个序列进行排序。它也很好地映射到GPU的编程模型。

排序网络的另一个有用属性是它们可以实现为电路。我们可以从直线程序的数据流图中获取此电路，或者通过将我们的排序网络图解释为与栅极的比较器的电路来解释为电路。通常，有多个分类网络映射到相同的电路。例如，将上面的重写规则应用于排序网络不会改变其对应电路。

这种电路可以在硬件中使用数字逻辑实现。事实上，早期的“电子数据处理”是第一次使用分拣网络：P. N. Armstrong，R. J. Nelson＆amp; D. J. O'Connor是第一个在1954年左右调查这一点的。在1957年提交的美国专利3,029,413“用N n线分拣开关分拣系统中描述了他们的观察。

就个人而言，我变得对排序网络感兴趣，因为它们可以用于编码SAT解码器时编码基数限制[4]。

如果我向您展示了一系列比较器或图表和声明，它们代表了一个排序网络，您如何验证或反驳此？一系列比较器，无需产生分类输出的要求，称为比较器网络，因此问题是我们如何识别所有比较器网络之间的排序网络。

一种方法是应用蛮力并尝试所有可能的输入。对于比较分类，只有元素的相对顺序很重要。这允许我们假设没有普遍性的，所以我们的输入序列具有在N N N通道的范围1，...，n 1，\ ldots，n 1，...，n的整数中的值。这给我们留下了N N N ^ N N N输入序列尝试。对于n = 27 n = 27 n = 27，这已经超过2 128 2 ^ {128} 2 128，因此这将仅适用于非常少量的通道。有几个参数您可以表明您只需要测试1，...，n 1，\ ldots，n 1，...，n的排列，从而将此编号减少到n！ n ñ！。这仍然很快而不是n = 45 n = 45 n = 45，我们需要尝试超过2 128 2 ^ {128} 2 128输入序列。

我们可以使用零一个原理进行更好的方式[8]。这是基于：计算最小和最大值随着固定单调3功能的应用，即F（min⁡（a，b））= min⁡（f（a），f（b））f（ \ min（a，b））= \ min（f（a），f（b））f（min（a，b））= min（f（a），f（b））和f（max⁡（ a，b））= max⁡（f（a），f（b））f（\ max（a，b））= \ max（f（a），f（b））f（max（a，b ））= MAX（F（a），f（b））当fff单调时。由于比较器计算最小和最大值，这意味着我们可以通过所有比较器网络推送或拉动固定单调功能的应用。现在假设我们拥有一个具有输入序列的网络，我们的网络不排序：

我们可以找到一对无序输出元素，这里是第二和第三，然后定义一个单调阈值 - 函数，可以将我们的值映射到布尔值4，使得较小的无序元素被映射到0 0 0和较大到1 1 1.在我们的示例中，我们可以使用f（x）= 1 f（x）= 1 f（x）= 1当x≥3x \ ge 3x≥3和f（x ）= 0 f（x）= 0 f（x）= 0否则。

如果我们将FFF元素施加到输出序列1,3,2,4 1,3,2,4 1,3,2,4，我们得到0,1,0,10,1,0,10,1：1 ，0,1，一般序列将保持未损害。

随着功能f f f f f是单调，我们还知道在应用比较器网络之前将其应用于输入，将导致相同的最终未输出输出序列：

这意味着对于显示比较器网络不是排序网络的每个逆示例，存在至少一个使用布尔输入序列的相应的反应示例。因此，尝试所有布尔输入序列，其中有2 n 2 ^ n 2 n足以验证排序网络。当然，指数增长仍然很多，但它在尝试所有排列方面是一个重要的改善，即使是n n n的相当小。仅关注布尔序列，也往往方便对分类网络的理论分析以及处理分类网络的算法的实际实现。

我们可以做得更好吗？事实证明，验证排序网络是CO-NP完整问题的验证，因此我们不知道一个明显更好的方法来验证适用于所有网络的工作。然而，在我的经验中，对于具有足够大量信道的网络，我们在寻找良好排序网络时遇到的大多数网络可以比使用基于CDCL的SAT求解器或BDDS或ZDDS更快地验证速度而不是蛮力。对于许多NP完整问题，这是这种情况，在那里，难以解决的问题不是实际兴趣的问题。然而，对于少量频道，严格强制通过2 n 2 ^ n 2 n输入的简单性很难击败。

虽然检查任意比较器网络是否排序网络不是很有效，但有几种系统的方法来构建排序网络。一种基于气泡排序算法的变型的非常简单的方法使用1 2 n（n - 1）\ frac {1} {2} n（n - 1）2 1 n（n - 1）比较器。这里的想法是N - 1 N - 1 N - 1比较器的序列可用于找到最大的元件并将其移动到最后，然后使用N - 2 N - 2 N - 2比较器移动第二个最大的元素到最终位置等，直到我们知道所有元素都被排序：

“可以通过利用n - 1 n-1 n - 1两条线分类开关并以这些开关连续地比较由位进入添加的输入端子的串联馈送的记录与N线分类开关的每个输出相对于优先级排序，例如：即，如果送入新输入终端的记录具有同时比较的所有记录的最高优先义，则它将被引导到最高优先级的输出端子。“

“在上述规划之后构造的N n N线分类开关通常不代表可能使用的两个线路开关的最小数量，特别是随着线的数量增加。通过使用技能，可以使用缩小数量的两行排序交换机来设计经济的N线分类开关。“

虽然纳尔逊＆amp; O'Connor的专利没有描述一种改进此的一般方法，RC Bose和RJ Nelson在1962年的1962年[3]中发布了这种方法，该方法仅需要O（n 1.585）O（n ^ {1.585}）O（n 1.585 ）许多比较器。

今天，在实践中构建排序网络的最佳方法是K. Batcher [2]的两种合并排序变量：Bitonic Merge排序和奇数偶数的排序。由于合并来排序它们都通过将序列划分为半数，递归地排序，然后使用比较器将两个分类的一半合并为单个排序序列。当只留下两个元素时，递归终止。可以使用单个比较器对两个元素进行排序。由于递归结构仅取决于输入尺寸n n n，因此可以完全展开成固定的n n n的直线程序，因此可以实现为分类网络。

合并排序需要对数递归深度，其中每个级别上的元素数概括为所有分支，保持常量。对于一般比较，其中操作顺序未提前固定，可以在线性时间执行合并，从而导致渐近最佳O（n log⁡n）o（n \ log n）o（n lo gn ）合并排序的整体运行时间。

事实证明，不可能使用固定网络使用线性数量的比较器来合并两个相等长度的序列。 5，而Batcher的两种算法在它们如何执行该合并操作中，则它们都使用递归划分和征服方法来实现。

他们究竟如何执行合并操作作为比较器网络，因为这篇文章脱离了范围，但我的参考是在Bitonic排序和奇数偶数的BITONIC排序和奇数甚至合并上的参考。

对于这两者来说，合并需要O（n log⁡n）o（n \ log n）o（n lo gn）比较器，导致o的总体大小（n（log⁡n）2）o（n（\ log n）^ 2）o（n（lo gn）2）。这比一个常规比较排序的最佳算法的运行时间速度速度速度速度快，但仅通过额外的对数因子。我会在大多数设置中说，其中排序网络是有利的，这第二个对数因子不太可能是Showstopper。

然而，事实证明，两种算法产生的网络的大小不是最佳的。早期使用系统手动试验和错误，在早期找到了用于小输入大小的更好网络。使用手动找到的网络，可以提高隐藏在BitOnic或奇数合并排序的大O O O中的恒定因素。为此，我们一旦输入大小低于固定输入大小阈值，我们就终止外部合并 - 排序递归。此时，我们使用小于持续的Merge-Sort的固定预计算机对输入进行排序。这导致为小输入大小找到更好的排序网络，即使我们仅对排序更大的序列感兴趣。

它还提出了最佳排序网络大小的问题，包括是否需要额外的对数因子。

这个非常称为Bose-Nelson分拣问题，在RC Bose和RJ Nelson之后发表了这个问题的第一次分析[3]及其O（n 1.585）O（n ^ {1.585}）O（n 1.585） - 议题建设。

在一段时间内，Batcher在1968年发布了他的第一算法[2]之前，甚至猜测O（n 1.585）O（n ^ {1.585}）O（n 1.585）是最佳的。多年来没有人设法发现具有比Batcher的O的更好大小复杂的网络（n（log⁡n）2）O（n（\ log n）^ 2）o（n（lo gn）2），所以它似乎像这样可能是最好的。因此，当M. Ajtai，J.Komlós和E.Szemerédi[1]发表了一个大小的尺寸网络（n log⁡n）o（n \ log n）o的建筑是一个大的惊喜（n lo gn）于1983年。他们描述的网络称为AKS分拣网络。他们的O（n log⁡n）o（n \ log n）o（n lo gn）尺寸与渐近的ω（n \ log n）ω（n \ log n）ω（n lo gn）ω（n log n）ω（n lo gn）匹配。一般比较的生长速度排序运行时间。由于这个下限也适用于排序网络大小的特殊情况，因此AKS网络具有最佳的渐近尺寸

那么为什么我在上一节中没有提到这一点，当它明确比Batcher的网络更好？一如既往地，大O O OS只讲述故事的一部分。如果隐藏的恒定因素太大，最佳的渐近生长速率没有帮助。并且大的情况在AKS排序网络的情况下，或者作为KNUTH放置它：“Batcher的方法更好，除非N n N n超过地球上所有计算机的总内存容量！” [8]。这使得AKS网络成为银河算法。

有更新的O（n log⁡n）o（n \ log n）o（n lo gn）结构[7]大大提高了恒定因素，但即使是那些，对于任何实际数量，Batcher的排序网络也会更小渠道。

尽管如此，我们确实有许多实际排序网络的实际排序网络，绝对术语，而不是使用Batcher方法产生的网络。我们只需有效地构建任意尺寸的有效系统方式。这使得重点关注排序网络的绝对尺寸，而不仅仅是它们的渐近生长。

除了用一般方法来构建任何大小的排序网络外，我们还可以尝试找到固定给定的通道N n n的良好排序网络。我们已经看到，回答给定的比较器网络是否是一个排序网络不是一个简单的问题，所以我们不应该指望这种情况。

对于非常小的n n n，系统手动试验和错误很好地运行，但从n = 13 n = 13开始，使用启发式计算机搜索找到最佳已知的网络，通常基于遗传算法。 Knuth的“计算机编程艺术”Vol。 3.列出N≤16n \ le 16n≤16的最知名网络。这些网络已知一段时间。除此之外，B. dobbelaere维护一个列表，包括最近的16个更新。 n≤3216＆lt; n \ Le 32 16＆lt; n≤32。

在使用系统试验和错误或启发式搜索时非常有效地发现良好的排序网络，您无法知道到目前为止找到的最佳排序网络是否具有最佳尺寸或者是否仍然可以找到较短的排序网络。

为了证明排序网络具有最佳大小，我们必须排除任何较小的网络的可能性。蛮力方法是枚举所有较小的排序网络，但这会非常快速地变得不可行。因此，我们需要找到一次排除许多较小排序网络的方法。

这样做的一种方法是比较种类的信息定义。尽管名称，但没有必要调用信息理论，小学组织足以说明它：有n！ n n n n n个不同的6个元素的排列，以及基于比较的分类算法必须需要区分所有这些。每个比较有两个结果，所以K k k比较有2 k 2 ^ k 2k可能结果。如果我们有更可能的结果，我们只能区分所有输入排列，因此我们需要有2k≥n！ 2 ^ k \ ge！ 2k≥n！或等效k≥¼log⁡2n！ ⌉k \ ge \ lceil \ log_2 n！ \ rceilK≥⌈10n！⌉。这也是我们如何导出ω（n log⁡n）\ oomega（n \ log n）ω（n lo g n）的比较排序的ω（n lo g n），如k≥log⁡2n！ ≥log⁡2（（1 2 n）1 2 n）= 1 2 n log⁡21 2 nΩΩ（n log⁡n）k \ ge \ log_2 n！ \ ge \ log_2（（\ frac 1 2 n）^ {\ frac 1 2 n}）= \ frac 1 2 n \ log_2 \ frac 1 2 n \ in \ oomega（n \ log n）k≥0

......