古代音阶问题
一句话摘要:我解释了为什么发明指数规模,以及它如何根据整数的比率与较旧的尺度进行比较。
本文是对音乐尺度的数学性质的延续。在那篇文章中,我们使用的比例来提出八度的划分。我们已经给了拉丁名称到音乐间隔(或频率比率):八度音程为2/1,特里亚5/4,Quinta为3/2,Quarta为4/3,音调为9/8,和半音作为16 / 15.
在美国ENG LISH中,TENTIA,Quinta和Quarta间隔熟悉为基本规模的第二,第三,第四,第五个音符。但是,由于前一篇文章中描述的原因,我将使用拉丁名称。 (俄语,这些更熟悉地称为Секунда,Терция,Кварта,Квинта。)
结合间隔时,我们“添加”它们,但在我们乘以它们的频率比方面。这是因为人类耳朵在对数标度上感知频率。平衡频率比,感觉像倍增音乐间隔。缩小音乐间隔对应于将其频率比率乘以小于1的数字。
例如,双延期间隔具有2/1 * 2/1或4/1的频率比。并且7八八八曲棍间间隔具有(2/1)⁷或128/1的频率比。
(对数刻度转换乘法添加。在本发明计算器之前,Men使用对数幻灯片规则来手动计算快速乘法。)
基于比率的所有要调整的方法都被称为语调调整。此外,只需调整的术语也可以指特定的PToLEMAic调整。这个名字背后的想法是音乐间隔最令人愉悦。
但是,根据比率调整仪器会产生不一致的仪器,因为没有单个单位从中构成所有间隔。作为一个类比,采用厘米混合英寸的情况。这些长度单位不一致。 (另一方面,英寸与脚一致,厘米是一致的米。)
例如,对于刚进行调整,例如,远离某个基本音符的注释12 Quintas与远离相同基本音符的注释7八张ock。它们之间的比率被称为“Pythagoras的逗号”,它可以像这样计算,
我们可以滥用“overtones”的概念来说,毕达哥拉斯逗号是一个遥远的531,440-th奖励,翻译524,288 / 2 ock下降。显然,这种纸条与基本笔记没有良好。这就是这种高度消失的间隔被称为“逗号”的原因。
“逗号”这个词来自希腊κόμμα,这意味着“切割行为”。这个名字背后的想法是消散声音是“切割耳朵”。虽然这种“逗号”间隔是理论上的可能性,但可以简单地避免音乐间隔?毕竟,为什么音乐作品有7个八度曲目范围?事实证明,逗号更普遍,很难避免。
5世纪的Tarentum的音乐理论教师Photalaus注意到,两种血症和胶石逗号结合在9/8的音调间隔。 (血红素是具有频率比256/243的间隔,它是音调的“半”的粘棒选项)。
Phelalaus的观察结果表明,如果根据毕达哥拉斯秤进行调整F#和G♭,则会在毕达哥拉斯逗号不和谐中进行冲突。 (这里的#和♭符号意味着通过血液瘤饲养和降低)。它有多大可能发生?因为某些乐器用“黑色”键调整为白色键的锐白尖锐,但其他仪器用“黑色”键调整为白色键的平面,这些仪器将在不和谐中发生冲突。
只有宗语调整中存在其他值得注意的逗号。在发出音符C,G,D,A,E,C以此升序和下降序列中播放时,PToLEMAIC逗号发生在称为“逗号漂移”,
笔记之间的频率比为3/2,3 / 4,3 / 2,3 / 4,4 / 5。 (对于上升方向,比率大于1,并且对于下降方向,比率小于1.)乘以它们的比例为81/80,PToLEMAIC逗号。序列被称为逗号漂移,因为原始基础笔记(这里C)漂移到一个令人失望的流氓“基础”注意。这种逗号也被称为苏格兰逗号。
当PTolemaic逗号与毕达哥拉斯逗号冲突时,会发生另一个不和谐。假设一个乐器播放GB而不是F#,导致毕达哥兰逗号531441/524288,另一乐器播放漂移的F#,导致PToLEMAIC逗号81/80。两个笔记之间的间隔是什么?间隔被称为“Schisma”,
Syntonic Comma 81/80也是Pythagorean特里斯和PToLemaic特里斯之间的间隔。来自Wikipedia文章关于Syntonic逗号:
毕达哥兰主要第三(81:64)和次要三分之一(32:27)被解剖,这阻止了音乐家使用三联网和和弦,强迫他们几个世纪以相对简单的质地写音乐。在中世纪晚期,音乐家意识到,通过略微磨损一些音符的音高,毕达哥拉斯三分之二可以是辅音。例如,如果e的频率由靴子逗号(81:80),C-E(主要第三)和E-G(次要第三)变为仅限。
因此,我们可以看到Syntonic逗号很重要。 19世纪的德国物理学家亥姆霍兹开发了一种音乐符号,表明应该由毕达哥拉斯调整注意应升高或降低了多少象征逗号。
通过重复Quintas(自身乘以3/2乘以3/2)来导出中世纪的毕达哥拉斯级,并通过八度曲目(除以2)。通过这种方式,衍生为(3/2)的频率81/64⁴除以4.我们如何修改该方案,以便为特图获得更高的5/4比率令人愉悦的5/4比例?如果我们将Quinta降低了四分之一的棘手逗号81/80,那么共有四个Quintas将通过完整的苏格兰逗号贡献总体减少。数量,
这一确切的方法是由16世纪的音乐家拍摄的,结果是奥基逗号的意思。他们牺牲了完美的声音Quinta(美国英语的“完美第五”),获得更好的探测特里迪亚(“主要第三”)。该规模在16世纪和17世纪中普遍存在。
如果我们将上方的两侧乘以4,然后采取第四根,我们有一个简单且透露的表达式,用于平凡的Quinta作为5的第四个根,
因此,这里我们看到了不调谐到整数的间隔的第一示例,但实际上是“非理性”编号。更稍后的更多信息。
基于比率的尺度限制是它们不允许调制。调制是指改变为从另一个基频开始的新八度度间隔。莫扎特和巴赫广泛使用调制。它在后来的音乐中普遍存在,包括爵士乐和流行音乐。以下是法国作曲家Charles-Henri Blainville的18世纪的报价:
调制是本领域的重要部分。如果没有它,有很少的音乐,因为一块源于它的真正的美丽,而不是从大量的固定模式,而是来自其调制的微妙面料。
例如,可以希望在A-to-a octave中开始一个歌曲,该octave具有440 Hz的基本频率,然后切换到D-to-d ockaive,其基频为440 * 4/3或586.66 ...... Hz。基本说明(或基本频率)称为补品或键。因此,一首歌曲可以从A的键开始,然后调制到D的键中。(不要将“钥匙”混淆在“滋补”的意义上使用,用一个压制的物理钢琴键。)
在只是语调调谐中,为了在一个新的补品的性能中调制,一个必须在某些情况下切换到另一个调整到该补品的仪器。这是为什么?在毕达哥兰调整(语气,音调,血液胨,色调,音调,音调,血液中)有时,必须将黑色键调整为远离前一张音符的音调,或者从先前的说明远离上述音符。一旦选择了黑键调整,就无法使用一些调色剂。例如,如果F#被调谐为E的音调(当D是TONC时,如果C是补品),则必须在C是补品时由半音提前E,然后F#永远不会是F的半音。但如果C#是补品,则需要后者。因此,如果可以调制到D的键,那么它不再可能模块到C#的键。
在PToLEMAIC规模中发生类似的问题。如果“a”是滋补频率,那么,比例是(音调,次要音调,半音,音调,次要音调,音调,半音)或数字(9/8,10 / 9,16 / 15,9 / 8 ,10/9,9 / 8,16/15)。让我们说我调整了钢琴键,以与补品一样匹配这种比例。现在,假设我假装B是新的补品,因为我想通过音调的色调培养整个音乐。备注(C#)之后的B必须是相对于B的音调的间隔。是吗?不,下一个间隔是毕达哥兰次要音调,即10/9。
在调制方面,PToLEMAIC规模比毕达哥兰秤更宽容,因为它具有不同尺寸的音调(9/8和10/9)。该观察结果表明,可以开发更宽容的调整的调谐,允许最大化可以在不重新定期仪器的情况下使用的不同调色剂的数量。这种规模是在17世纪开发的,它被称为良好的钢化尺度。
由于该术语在17世纪中使用,“良好的锻炼”意味着标准键盘的每个八度音录的十二张笔记被调整,以这样的方式可以在所有主要或次要使用的主要键中播放音乐,它不会听到曲调的声音(Duffin 2007,37)。
唯一的调制方式可以不受限制地工作,如果是从重复的小间隔组成的所有间隔。但是,这是不可能的使用比率。 BCE的4世纪Tarentum的Pythagorean哲学家Archytas表明,没有“A”和“B”的解决方案,作为整数到方程式,
当N等于1.Archytas的结果时,等式右侧的表达为2/1,表明不可能以更小的比例表达2/1作为重复产物。
(作为两个整数的比例表示的数字被称为数学中的“Rational”。相反,如果一个数字不能以这种方式表达,则它被称为“非理性”。这些术语不与含义混淆哲学中的“理性”和“非理性”。)
良好的钢化尺度是上面描述的短四分之一逗号规模的问题的答案。为了允许调制,钢琴的所有白色和黑色键的意风尺度定义的频率,其中有12.名称“卑鄙音”之后的想法是所有音调大致相同的平均大小。每个黑键的值是由狭窄的意思Quintas和ocvaves的组合导出的。如果我们将D作为补品,那么通过Quintas在两个方向上移动时,发现黑键,如下所示:
例如,将D作为补品,让y成为5的第四根。(回想一下,这是平凡Quinta的频率。)然后在同一八度音程中进行D的黑色键E♭调整为8 /Y⁵ 。预先生制D的黑键C#被调谐到Y⁵/ 8。我们预计两个相邻的黑色键之间的间隔是一个音调间隔。让我们检查:它们之间的比率为64 /Y¹⁰。分母Y¹⁰为2.5的功率为约55.9。因此,间隔具有大约640/559的频率比。这是否接近预期的“只是”音调间隔为9/8?相应的十进制扩展为1.1449 ......和1.1250。
如您所见,两个相邻的黑色键之间的间隔不是9/8。它至少是与此规模中的两个白色键之间的间隔相同吗?不可以。比例相对于滋补D将e设置为y²/ 2的频率。在十进制中简化为5,或1.1180的一半平方根。正如您所看到的,这是一种不同的语气。
如果我们试图决定与♭和g#有关的事情,事情会变得更多。它们是同一个纸条吗?它们被计算为具有不同的频率,但计算将它们放置了几个八度八页。当他们在同一个八度音程时应该如何调整?如果我们通过八度音录转换较低的音符,并且八度音录的较高音符,它们将以D Tonic的八度间隔符合。 (好奇地,下转置的G#低于上转置A♭)。在这种情况下,较高频率与较低频率之间的比率为128/125,这被认为是曲调,因为它小于半音的一半。 (西方音乐没有小于半音的间隔,但在东方音乐中发现了这样的间隔。)
如果我们摆脱了G#,只需按ocvaves将其转发到ock替换G#S,那么我们就会有一个新问题。新的G#现在进一步来自下面的音符,特别是它远离C#。在改变之前,间隔C#和G#是平凡的Quinta,但现在它既不是完美的Quinta也不是平凡的四分之一 - 逗号减少的Quinta。这是另一种古塔。这种新的间隔被称为“Wolf Quinta”(俄语:Волчьяквинта)或美国英语术语中的“狼第五”。它有这个名字,因为它会导致独特的节拍,听起来像狼嚎叫。
总之,意义的四分之一逗号规模将在某个地方有一个狼Quinta,并且该地方取决于仪器被调整的中心注意的选择。这取消了这种仪器上的许多其他调色剂。 (在我们的示例中D是中心注释。)所以,音乐家无法调制其他调子,这必须具有音乐中的C#-G#组合。 (例如,您无法播放具有Notes C#-e-G#-B的E6 / C#Chord。)
如果Quintas反复向下会达到Quintas重复向上(八度音阶后),然后他们会创建一个“Quintas圈”(以美国英语称为“五分之圈”。)唉,在季度不会发生逗号意味着规模,导致狼的间隔,正如我们所看到的那样。
作为对这些困难的回应,16世纪的andreasWerceister建议创造一种良好的钢化尺度,这将产生这种封闭的Quintas圈子,同时保留在其他尺度中发现的理想品质。来自维基百科:
[WERCKMEISTER]描述了一系列调整,其中增强臂注意具有相同的音高:换句话说,使用相同的音符作为(例如)e♭和d‖,从而“将键盘带入圆圈的形式”。这是指音符或键可以布置在第五个圆中,并且可以独立地从一个键调制到另一个键。
术语“良好的锻炼”是一种具有可能非平等间隔的各种调整的伞长术语,其目的是最大化调节调谐的能力。此外,在不同的滋补品中扮演不同的偏差结合。间隔,它给出了独特的纹理,在该钥匙上玩。维基百科提供了这一现象的良好综述:
术语“良好气质”或“良好的气质”通常意味着一些不规则的气质,其中脾气暴躁的五分之一不同的尺寸,但没有键具有非常纯度的间隔。历史不规则的速度通常具有在普通的第三个(“Naturals”)之间的最窄五分之一,并且在彩色纸张(“锐利和单位”中宽五个)。然后每个键都有一个稍微不同的语调,因此不同的键具有不同的字符。这种“关键颜色”是18岁和19世纪和19世纪和19世纪音乐的重要组成部分,并在该期间的论文中描述。 [我的重点]
关键的现象是选择气质概念来描述调整系统的原因。选择的“气质”通过它来调整钢琴或交响乐或管弦乐队调整其乐器的钢琴,已经确定了所扮演的音乐作品的明显质地,气质。也就是说,音乐作品可以通过不同的键调节,在每种情况下产生不同的键颜色,但整体效果被调谐的整体气质覆盖。
(具有讽刺意味的是,拉丁语中的单词气质意味着“混合物”,这可能是各种间隔和频率的混合物的名称。然而,心理气质,但是,Wikipedia写道,气质“广泛地指的是持续的行为持续的个体差异在生物学上是基础的,并且是相对独立的学习,价值观和态度。“这是不正确的,因为人的性格,因此他的行为,由道德决定,从而通过自由意志决定。然而,生物差异确实影响了速度不同的人体验情绪。有些人会迅速反应,情绪很快就会消失。其他人会反应较慢,情绪持续更长时间。据推测,那些快速反应的人有更快的情绪。)
几个人发明了良好的钢化调整版本。如上所述,Werkminster开发了其中一个。托马斯年轻,18世纪的物理学家也是如此。另一个是由J.S.的学生开发的巴赫,Kirnberger。物理学家惠更斯(17世纪)写了一封“关于谐波循环”的信,其中他描述了八度音高的31倍。
然而,最成功的“良好的回火”量表,是平等的气质。当物理学家Simon Stevin在17世纪发明了平等的钢化尺时,西方音乐看到了戏剧性的转变。此规模使调制调制到任何键,并通过放弃完全“合理的”频率比率来解决。
但解决方案很容易作为千根的千根。什么应该是“k”?我们应该将八度音拆分为12个音符(k = 12),或者我们应该将其分成11或13条票据吗?
毕竟,我们为什么首先有12个音符? Diatonic Scale(Famiar“主要规模”)将八度音得分分成7个间隔。但是需要更多的细分来允许使用其他基本票据进行调制。 (细分器在钢琴的黑色键处制作。)具有合理的频率比率,足以提出12个细分,试图使它们保持甚至和多才多艺。但是,在使用指数时,我们可以自由地将八度音程细分为任何数量的平等间隔。
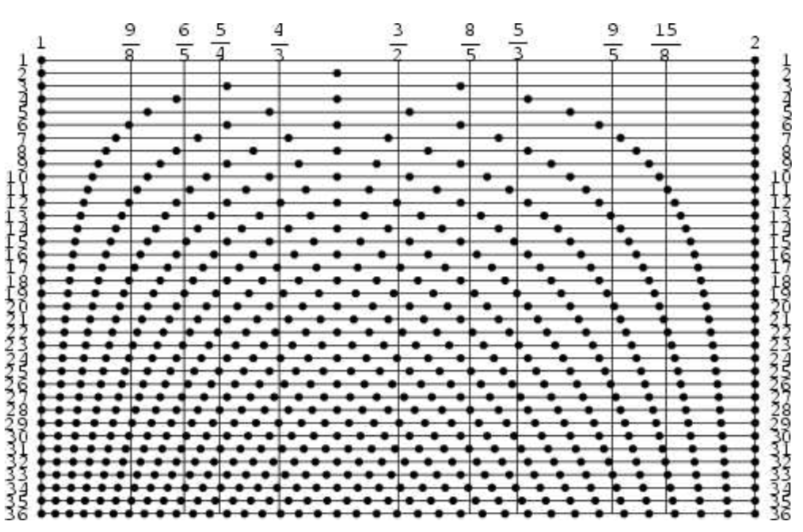
Stevin确实选择k为12,导致每个八度的熟悉的12个色键。但是,另一种选择是可能的吗?如果我们作为指导原理“只是”间隔9/8的指导原理,则需要5/4,所以为特里菊可望,并且对于Quinta期望3/2,然后我们应该至少希望指数细分将产生靠近这些值的组合。
这是一个图示了水平线上的k-th根,只有相交垂直的语调间隔。在线12中,点靠近垂直线。这意味着当划分的数量为12时,所得到的频率距离通过仅限于语调方案来预测的那些。因此,12个半音等气质刻度,似乎是分区成相等的良好方案。
这种比例或调整也在若干名称和缩写:12-TET代表12个半色调等气质,或12-ET,或12-EDO,用于同等分割的速度,或者自12划分以来的平衡等气质。是西方音乐中唯一广泛的变种。 “回火”这个词也与“气质”互换使用。
在刚刚的语调频率之间的新未开发的声音中除以12个以上的结果。 7/4的蓝调笔记
......