超级确定性可以调和量子和相对性

自从100多年前的概念以来，Quantum Mechanics有令人毛骨悚然的物理学家。虽然一些疑虑，例如不行，仅仅是美学，量子力学有一个严重的缺点：它缺乏测量过程的物理描述。这种“测量问题”表示量子力学至少是一个不完全的理论 - 就它而言，但缺少一块或更自然地，需要完全大修。在这里，我们描述了一种可以提供此寻求的完成或更换的方法：超级确定性。超级确定性理论是违反统计独立假设的理论（隐藏变量的分布与测量设置无关）。直觉表明，统计独立性是任何科学理论（从不介意物理学）的基本成分，而且由于这个原因，超级赛义目通常在Quantum基础的任何讨论中迅速丢弃。本文的目的是解释为什么现有对超级季度的异议基于古典物理和线性系统的经验，但这种经历误导了我们。超级季度是一种有希望的方法，不仅要解决测量问题，而且还要了解量子物理学的表观非局部性。最重要的是，我们将讨论如何以（几乎）模型独立方式测试该假设。

直到20世纪70年代，物理学基础的进展意味着分别在更高的能量或短距离处发现新的现象。但高能量物理学的进展已经放缓，并且可以在涉及物理学的深处基本问题方面进行课程。在过去的几十年中，物理学家没有成功地解决他们领域基础的任何开放问题;实际上它甚至不清楚我们越来越清楚，我们越来越靠近解决它们。最值得注意的是，我们仍然没有成功地合成量子和引力物理学，或者在解开暗物质的性质，自20世纪30年代以来已知的问题。

在这种情况下，回去看看我们没有采取的道路是有意义的，我们早早在那个看似死胡同的错误转弯。我们在这里争论的转弯是解决量子力学的缺点。至少，我们需要对估计量子测量的非线性度的测量过程的物理描述。

这条道路仍然在很大程度上未开发的主要原因是在相当一般的假设（下面定义）下，任何解决与相对性原则一致的形式中的测量问题，使得不可能独立于稍后的探测器制定状态衡量它。如果一个人不愿意接受这种依赖，那么通过贝尔＆＃39;圣经[1] - 一个必然必须得出结论，不可能的局部，确定性地完成量子力学完成。然后，这要求我们放弃一般相对性的原则，并增加了我们与其他相互作用的重力协调的难度。

如果一个是，相比之下，愿意接受现实主义的后果，还原主义和决定措施，一个人导致了一个理论，其中实验的准备状态永远不会与探测器设置无关。这些理论被称为“超级确定性”。我们希望强调超级确定性理论不是对量子力学的解释。相反，它们比量子力学更基本的理论，可以从中获得量子力学。

超级确定性经常被视为实验上未纯粹的漏洞（参见例如，[2]），其中一个人可以确定地解释所观察到的钟声和＃39;不平等。然而，由于各种原因，许多物理学家认为超级季度是一个非启动者。例如，他们认为超级确定性会将实验者转化为无意识的僵尸，无法自由配置实验装置。类似的论点具有，超级赛义目意味着在被认为是独立的过程之间的难以置信的阴谋存在。或者，它似乎会导致在时间向后传播。最重要的是，它被要求保护，超级赛义目将致命地破坏科学的概念作为客观的追求。简而言之，超级确定性被广泛认为是在水中死亡。

本文的目的是重新审视针对超级季度的论据。我们将争辩说，而不是成为一个难以置信和辨别的漏洞，超级季度主义的被忽视的选择是前进的方向;它＆＃39;我们没有服用的道路。

通常教导的方式，量子力学对其动态法具有两种成分：薛定草方程和测量处方。测量处方是探测器特征甾酸盐上的投影，然后将新状态重新归一成至1。

该测量处方（有时称为波浪函数的“更新”或“更新”或“崩溃”不是一体化操作。它通过施工保留概率，但它既不是可逆也不是线性的。缺乏可逆性并不是一个严重的问题：人们可以将不可逆转性解释为非物理限制，其中一个人忽略了小但有​​限的残留物，否则会使测量过程可逆。

相反，测量过程的主要问题是它是非线性的。如果我们有一个准备的初始状态|ψ1>将探测器带入尖端|χ1>，并且另一个初始状态|ψ2>将探测器带入尖端甾酸盐|χ2>，那么线性演化法将带来叠加（|ψ1> + |ψ2>）/ 2进入探测器特征符合的叠加 - 但这不是我们观察到的。

这是有问题的，因为如果量子力学是描述基本粒子的行为的正确理论，那么应该从中衍生出探测器这样的宏观物体。问题不仅仅是我们不知道如何制作这种衍生，它＆＃39;也更差：测量过程的观察到的非线性告诉我们，测量假设与线性Schrödinger方程相矛盾。

但是，有一个简单的解析这个非线性问题。在其密度矩阵形式中，Schrödinger方程非常类似于经典的Liouville方程。在这种形式中，Schrödinger方程有时被称为Schrödinger-liouville或Quantum-liouville方程，尽管历史上更正确的术语是von neumann-diac等式：

这里，H是系统的古典/量子汉密尔顿山，花括号是泊松支架，方括号是换向器。 ρ分别是经典/量子（概率）密度。

典型的Liouville方程在概率守恒的概率密度中是线性的。但是这种线性物质没有任何关于概率密度衍生的潜在系统的动力学是线性的。因此，例如，尽管它们是非线性动态的，但混沌动态系统，遵守概率密度的相同线性方程。对我们来说，两个方程之间的这种紧密的形式相似性强烈建议，量子物理学也是底层非线性确定性系统的线性概率描述。

从这个角度来看，追求everettian对量子物理学的方法并不是正确的事情，因为这个想法是为了信念，即薛定草方程是基础的;没有什么是依据。此外，在状态转移变得不可忽略的情况下，仅将非线性动力学附加到Schrödinger方程中的非线性动力学，因为它不是需要变得非线性的Schrödinger方程本身。自发折叠模型无论是不是确定性的1.试验波理论都在某种意义地解决了确定问题。然而，量子力学的试验波制剂基于明确的非局部本体论，并且这种非本地性能使得难以调和具有特殊相对性的这些理论，并且具有量子场理论。

那么，它需要用一个确定性，局部理论来描述量子物理，这是解释主义的意义，理论允许我们从理论的行为中获得探测器的行为和＃39;原始元素的行为？ Pusey-Barrett-Rudolph（PBR）定理[3,4]告诉我们，这种理论必须违反制备独立假设，根据该理论，复合系统的状态空间可以被描述为其因素独立的产品状态彼此。违反准备独立性需要构成产品状态的系统彼此相关，或者复合系统不能被描述为开头的产品状态。这种在制备的状态和探测器之间缺乏独立性是超级确定性的标志。

我们将超级确定性理论定义为psi-遇到的确定性理论，违反统计独立性，而是在尊重行动连续性的意义上是本地的[5]，即，由于爱因斯坦所说，没有“距离距离”。在本节的剩余部分中，我们将解释这些词的意思。

1. psi-emistex：一个理论是psi-认知意味着Schrödinger方程（或密度 - 矩阵）中的波浪本身本身并不对应于现实世界中的一个对象，即，不是Ontic。哥本哈根解释和新哥本哈根解释是Psi-exiStex，因为它们假设波浪函数只是对系统的状态进行了编码，而不是对应于系统的属性。然而，理论也可能是PSI-认识的，因为该波段是紧急的，例如作为更基本理论的统计表示。我们将在此处处理的理论是后者意义上的PSI-认识。

不用说，在任何这种理论中得出的波段应该遵守薛定草方程，其达到电流测量精度，因此再现了量子力学的远足测试预测。但当然，寻求一个从中获得量子力学的理论的程度不是重现量子力学，而是使预测超出到这一点。

2.确定性：通过确定性，我们将意味着理论的动态规律在时间t唯一地映射到任何T和T'时的时间t'。然后，可以反转此地图。

由于我们寻找的理论应该是决定性的，并且波飞行功能来自它，我们正在处理所谓的隐藏变量理论。我们可以询问这些隐藏变量的究竟是什么，下面的是由符号λ共同表示。答案取决于特定模型，一个是处理的，但松散地说λ包含确定测量结果所需的所有信息（除了状态准备的“不是隐藏”变量）。在这张照片中，量子力学根本不是确定性，因为我们不知道λ。

重要的是要认识到，这些隐藏变量不一定是一个措施的粒子内的属性或本地化的属性;它们仅仅要确定测量结果。要查看区分，请考虑以下示例。你站在医院的新出生病房里，看看一个充满尖叫婴儿的房间。在你的脑海中是两个问题：他们的血型是什么＆＃39;他们会爬上珠穆朗玛峰吗？在确定性理论中，对这两个问题的答案在当前在宇宙的状态下被编码，但在信息可用性方面非常不同。婴儿＆＃39; s血型在婴儿内局部编码。但是有关婴儿是否将继续攀登珠穆朗玛峰的信息分布在婴儿出生的那一刻的大部分时间内。在任何有意义的意义上，它不是婴儿的内在财产。该示例还示出了仅仅因为理论是确定性的，其时间演化不一定可预测。

3.违反统计独立性：超级确定性理论的最独特特征是他们违反了统计独立性。正如通常表示的那样，这意味着隐藏变量，ρ（λ）的概率分布不合于检测器设置。如果我们表示在钟实验中的两个探测器的设置为A和B，我们可以将此写成

例如，在CHSH版本的贝尔＆＃39; s定理[6]，a和b各自采取两个离散取向之一，我们可以在这里表示为0或1.派生贝尔＆＃39;不平等，一个假设ρ（λa，b）=ρ（λ），通常也称为“自由选择”（本术语是深刻的误导，因为我们将在第4.1节中讨论）。

虽然将统计（IN）依赖性作为数学需求写入统计（in），但对这种假设的物理解释不太清楚。可以诱惑将ρ编码的概率读为在现实世界中发生的（λ，a，b）的不同组合的发生频率。但是，如果没有关于我们正在处理的理论的进一步信息，我们不知道在现实世界中是否发生了任何特定组合。例如，在一对缠绕的颗粒被唯一λ标记的情况下，对于任何值，对于A和B的任何值实际上将在现实世界中实现。

至少，这些隐藏变量和探测器设置的这些替代组合是否存在于理论的状态空间上，以及是否在该状态空间上是遍历动态演化。很容易想到在状态空间上的Lebesgue措施方面没有ergodic的情况。以典型的非线性系统为例，如标志性Lorenz模型[7]。这里，渐近时间进化受到分形测量的吸引子的限制，其尺寸低于全状态空间。对于吸引子上的初始条件，从未意识到了大部分状态空间。

我们也不能将ρ解释为贝叶斯意义2中的概率2，因为它会编码代理的知识，从而要求我们首先定义“知识”和“代理”是什么。因此，这种解释将带回我们删除的困难，即观察者的成分的基本理论应该让我们衍生宏观概念。

因此，我们不应该将统计独立解释为关于现实世界的属性的陈述，但是将其理解为我们正在处理的模型的数学假设。这一点是隐含的，至少是贝尔本人[1]：

“我衷心坚持在这里分析各种物理理论，一方面，另一方面是关于独特的现实世界的哲学。在这个因果关系的问题中，它是一个巨大的不便，现实世界只给我们一次。如果有不同的东西，我们就无法知道会发生什么。我们不能重复一个改变一个变量的实验;时钟的手将移动，以及木星的卫星。在这方面，物理学理论更加适合。我们可以计算在理论中改变自由元素的后果，他们只是初始条件，因此可以探索理论的因果结构。我坚持认为[贝尔＆＃39; s定理]主要是对某些类型的理论分析。“ （强调原始）

总之，统计独立性不是通过观察或通过实验直接测试的东西，因为它隐含地借鉴了反事实情况，我们不观察到的数学可能性，这取决于一个＆＃39; s＆＃39;模型或理论，可能或五月不存在。

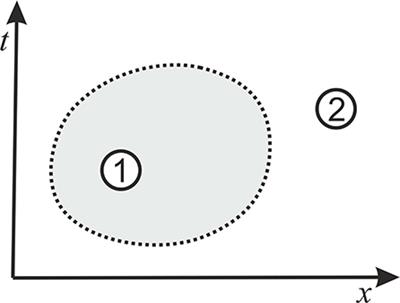
4.地方：最后，我们将假设超级确定性理论尊重行动的连续性（对于术语的广泛讨论，参见沃顿和阿格拉曼[5]）。动作的连续性（以下，CoA）意味着将信息从一个时空区域传送到另一个时隙，区域，相同的信息也必须存在于第一区域周围的任何闭合（三维）表面上的（参见图1 ）。这里的信息是指在本地可测量的数量。我们提出了这一假设，因为一般相对论和量子域理论都尊重该标准。

图1.行动的连续性。如果来自事件1的信息可以影响事件2，则此信息必须影响大约1个关闭的三个表面。

正如沃顿和阿格拉曼[5]中所规定的那样，COA的局部定义并不像进入贝尔＆＃39的地方假设一样强大。除了统计独立之外，贝尔＆＃39;定理的假设是

该假设指出测量结果由隐藏变量，λ确定，并且隐藏变量是远距离测量结果之间的统计相关的起源。正式地说，检测器A的测量结果的分布不依赖于检测器B处的结果XB的分布，反之亦然，即ρab（xa，xb | a，b，λ）=ρa（xa | A，B，λ）ρb（Xb | A，B，λ）。

参数独立性表示，一个探测器的测量结果的概率分布不依赖于其他检测器的设置，即它们可以写为ρa（xa |，b，λ）=ρa（xa | a， λ）和ρb（xa |，b，λ）=ρb（xb | b，λ）。

这两个假设在一起也称为“分解”。观察到违反贝尔＆＃39; S不等式，那么暗示必须违反所需的三个假设中的三个假设中的至少一个。量子力学尊重统计独立和参数独立性，但违反了结果独立性。超级确定性违反了统计独立性。钟型测试不能告诉我们两个选项中的哪一个是正确的。

所有三个贝尔＆＃39;定理统计独立，产出独立和参数独立性的所有三个假设 - 有时是统称为“局部现实主义”或“钟线”。然而，贝尔＆＃39;局部现实主义与术语“地方性”在一般相对性或量子场理论中使用的情况几乎没有做，这是由COA捕获的更好的。因此，已经提出了钟局部应更好地称为贝尔可分离性[9]。但是，那个术语没有抓住。

如何分解是一种合适的编码方式的方法和因果关系类似于解释统计独立性的问题：它吸引了可能实际发生的现实的替代版本。因子要求我们询问一个地方测量的结果是什么，在其他地方（结果独立）或者一个探测器的设定将具有另一个探测器的设置是什么＆＃39; s设置不同（参数独立性） 。这些是虚拟变化，表示为状态空间扰动。因此，更改不一定是指在时空中发生的真实事件。相比之下，行动的连续性是关于在时空中发生的过程的陈述：其定义不一定会调用反事实世界。

以较少的数学方式制作这一点，想象牛顿拍手，听到从他的墙壁反射的声音

......