使用锈病的划痕（计算机视觉教程）相机校准

相机校准通常被理解为估算影响真实3D场景图像的相机的特性的过程。其中的原理是透镜的有效焦距，其给定相机位置和场景图像的图像提供广角或伸缩性。有多种型号用于描述相机的图像形成行为。有些是具有少数组件的大多数线性方程相对简单，并且仅适用于描述简单的相机系统。其他是高度非线性的，具有具有许多系数的高度多项式。无论相机模型如何，人们都可以使用本文中的技术来校准其相机。

创建校准模块不是小任务;因此，我们＆＃39; ll将此博客贴在三个部分中。第一个部分将专注于校准背后的理论。第二部分将揭示数学，校准背后的原则，并展示了创造自己的方法的路线图。最后，第三部分将显示自式校准模块的结果，描述模块如何到达有用的结果。对于代码，您可以在此处遵循，或者在Tangram Visions博客存储库中访问本教程的完整代码库。戴着说，让＆＃39;潜水。

有许多现有工具可以用于校准相机。这些都存在作为独立程序和SDK库。鉴于此，为什么要写自己的相机校准模块？有一些真正的理由这样做，例如：现有工具可能不支持您要使用的硬件平台或参数相机型号。除了任何实用的动机之外，通过相机校准过程是有用的，以便更好地了解当您使用OpenCV等工具时发生的事情。当试图了解为什么这些工具中的一个可能不产生合适的校准时，这尤其有用。

相机校准基于线性代数，3D几何和非线性最小二乘优化的基础。人们不必成为所有这些领域的专家，但是必要的基本理解。为了保持合理的长度，3D变换的一些知识，3D变换，多变量的微积分和优化（能够理解成本函数的优化（能够理解成本函数）的技术是为了制品的结果。

代码片段（主要部分在第二部分）将在RERR中，我们将使用Nalgebra Linear代数箱和argmin优化板条箱。这里可以找到整个例子。

首先，我们需要一个图像形成的数学模型。这提供了一种紧凑的公式，其大致描述了场景中的3D点与图像中的相应的2D像素，AKA图像形成或投影的关系。预测通常以下列方式思考：

如果存在镜头，镜头将折射（即重定向）将它们指向的光线引导到在曝光时段期间测量入射到它们的光的各种像素。

一种这样的模型被称为针孔模型，该模型描述针孔摄像机和Camerae Obsolae的图像形成。由于其简单性，我们将为这篇文章使用此模型。

针孔模型可以为具有简单镜头的摄像机工作，提供它们的高度直线，但大多数摄像机展示了某种镜头失真，在这样的模型中未被捕获。值得注意的是，大多数相机型号忽略了很多镜头的真实寿命复杂性（焦点，折射等）。

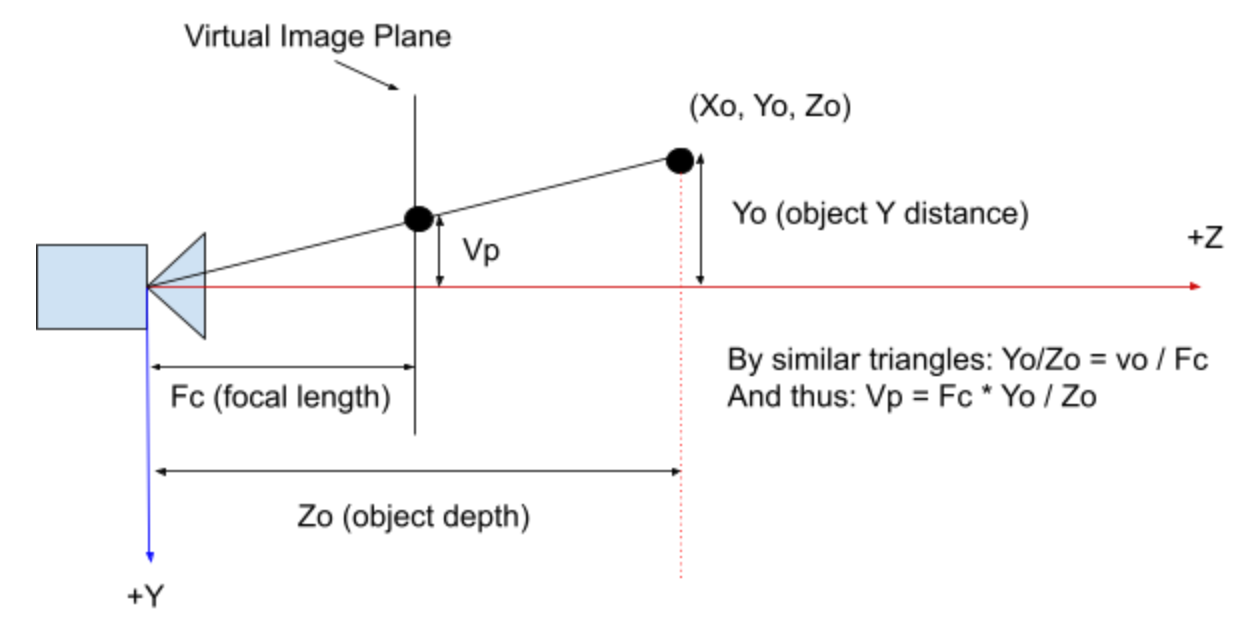
在针孔模型中，据说相机位于下图中显示的相机坐标系的起源。要以图像为3D点，您可以在问题和相机之间绘制一条线，并查看该线的位置与虚拟映像平面相交，这是相机＆＃39; S物理传感器的模型站立。然后将该交叉点切换并根据传感器分辨率转换并缩放到像素位置。在该模型中，在称为焦距的距离处，在相机（即沿+ Z轴）的前面设置的图像平面。

从该图中导出交叉点的公式的技巧是一次考虑两个维度。这样做暴露了平面上的点之间的类似三角形关系和场景中的点。

图像平面不是完全抽象的概念。它代表了相机的实际CMOS传感器或薄膜。交叉点是该物理传感器上的一个点;因此，从该传感器上的点（例如米）的距离为单位以距离为单位来描述\\（U_ {平面} \\）和\\（v_ {平面} \\）。需要将该平面位置映射到实际像素的进一步转换。

主点：像素的Z轴映射上任何点的像素位置。主要点（\（c_xx，c_y \））通常位于图像的中心（例如，用于640x480图像的像素320,240），但由于小的缺陷，通常略微偏离。

主要点占像素空间原点和交叉点之间的差异。 z轴上的交叉点将具有零x和y组件，因此将项目项目投影到\\（（u_ {plane}，v_ {pherl}）=（0,0）\\）。同时，像素空间中的原点是传感器的左上角。

它在计算机视觉缩略图中是常见的，以将焦距和像素间距术语分组为一个像素单元焦距项，因为它们通常为给定的相机（假设镜头无法缩放）固定。对于x和y尺寸的不同的焦距参数也很常见，\\（（f_x，f_y）\\）。从历史上看，这是为了解释非方形像素或外来镜片（例如变形镜片），但在许多情况下，具有两个焦距参数并不是很好的动机，甚至可以是有害的。这导致针孔模型最常见的形式：

$$ \ begin {bmatrix} u_ {pix} \\\ v_ {pix} \ neg {bmatrix} = p（\ bar {x}; \ {f_x，f_y，c_x，c_y \}）= \ begin {bmatrix} f_x \ frac {x} {z} + c_x \\\ f_y \ frac {y} {z} + c_y \ end {bmatrix} $$

我们希望使用相机校准估计的系数\\（f_x，f_y，c_x，c_y \\），因为我们将在本系列的接下来的两个部分中显示。

FN项目（参数：＆amp; Na :: Vector44＆lt; / * fx，Fy，Cx，Cy * / Pt：＆amp; na :: point3＆lt; f64＆gt;） - ＆gt; na :: point2＆lt; f64＆gt; {na :: point2 ::＆lt; f64＆gt; :: new（params [0] * pt.x / pt.z + params [2]，// fx * x / z + cx params [1] * pt.y / pt.z + params [3]，// fy * y / z + cy）}

此时，我们解释了相机校准后的理论。我们＆＃39; ll在这里休息一下，并返回第二部分，我们潜入原则，大部分数学，以及了解创建校准模块所需的一些代码。