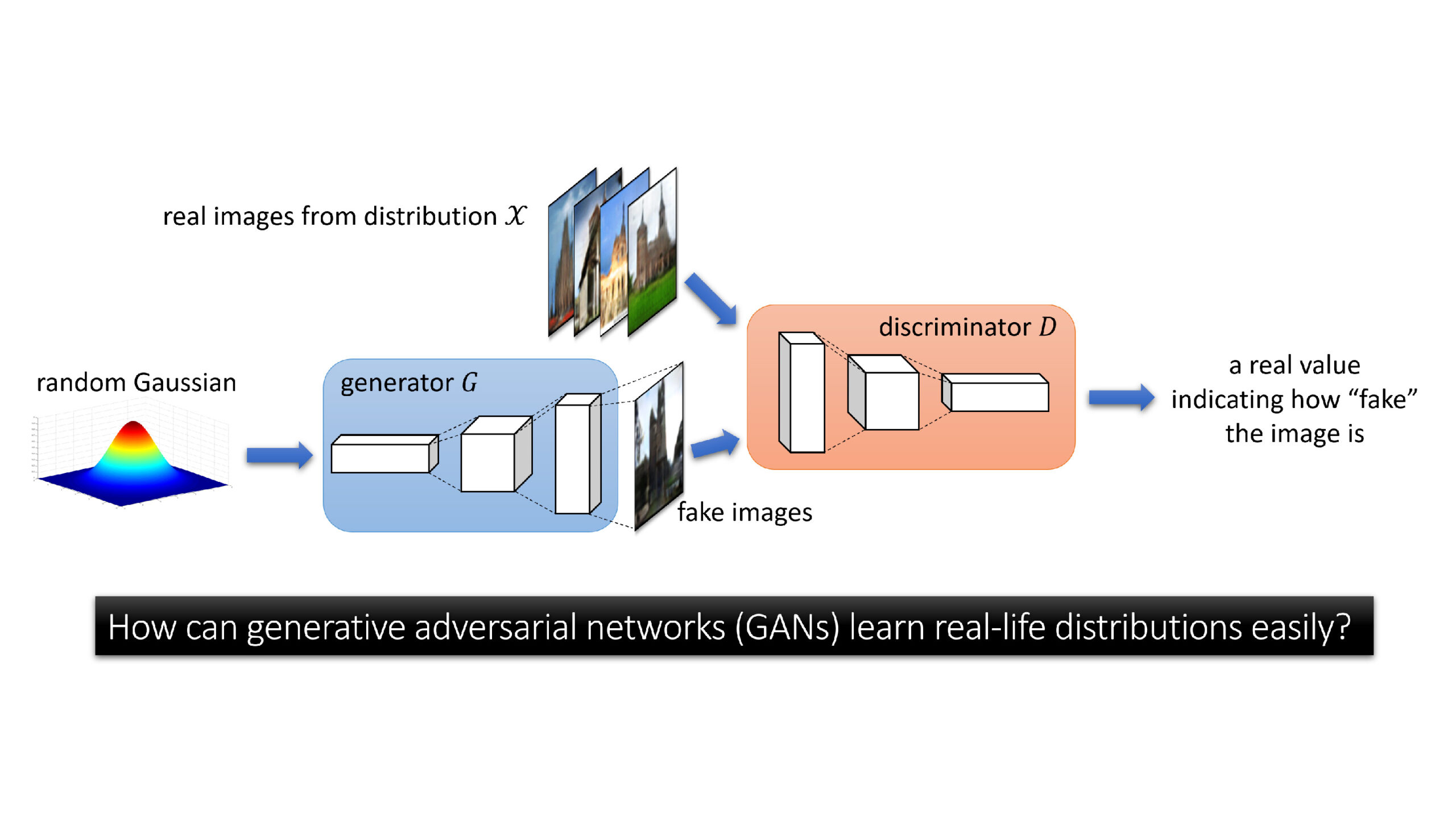
Gans轻松学习现实生活分布

一种生成的对抗性网络或GaN是Goodfellow等人提出的最强大的机器学习模型之一。用于学习从复杂的现实世界分布中生成样本。 GANS已经引发了数百万的应用程序，从产生了逼真的图像或卡通人物到图像到图像翻译。 Tying奖奖Laureate Yann Lecun叫Gans“最近10年来最有趣的想法。

在生成图像的背景下，GAN由两部分组成。 1）采用输入\（Z \）的参数化（Deconvolulate）生成器网络\（g \），其是随机高斯向量，并输出假图像\（g（z）\）。 2）参数化（卷积）鉴别器网络\（d \），其作为输入图像\（x \）并输出实值\（d（x）\）。要学习图像的目标分布\（\ Mathcal {x}），GAN的培训过程涉及找到一个发电机\（g \）（通常通过梯度下降升级），其中分布\（g（z）\）假图像与实际图像的分布\（\ Mathcal {x}）无法区分，使用其参数系列中的任何鉴别器\（d \）。我们说明了图1中的GAN。

与大实证成功鲜明对比，GaN仍然是理论上最不理解的机器学习模型之一。发电机如何将随机向量从非结构化球形高斯分布转移到高度结构的图像？如何通过当地搜索算法（如梯度下降Ascent（GDA））来找到发电机？判别在培训过程中的作用是什么？

所有这些理论问题仍然没有答案。这可能并不令人惊讶，因为即使学习一些已知的分布的线性变换也可以计算地硬化（即使是最坏的情况下的NP - 硬），更不用说学习通过Relu激活的神经网络给出的转换。

这是否意味着GaN理论达到死胡同？不可以。要了解GAN的巨大经验成功，我们的新论文“前瞻性超级分辨率：如何将GAN学习现实世界分布的分层生成模型”，调查现实世界分布的特殊结构，特别是图像结构，了解GAN如何有效地超越最坏情况，理论界。

大多数现实生活图像可以在不同的分辨率中查看而不丢失语义。我们经常可以将1080p轿厢图像的分辨率降低到小于16像素，同时仍然保持可以由人类识别的汽车的轮廓。

因此，人们可以期望用于现实寿命图像的渐进生成模型 - 利用发电机的下层产生图像的下分辨率版本，以及产生更高分辨率的更高层。 NVIDIA研究人员Karras等人对该进步生成模型进行了实验验证，并且还在下面的图2中说明。

在这项工作中，我们深入了解了这种图像的结构属性。我们将其正式形式化为前瞻性分辨率财产。在数学上，我们考虑学习如下逐渐生成的图像的分布。让\（x_1 \），... \（x_ {l-1} \）是较低分辨率的\（x_l \）的图像（可以通过图像下缩放从\（x_l \）计算），分辨率\（x_1 \）是最低（例如8×8），并且\（x_l \）的分辨率最高（例如128×128）。我们假设用隐藏的图层\（g ^ * \）（要学习）\（s {_1 ^ *} \），\（s {_2 ^ *} \），...，\（s {_L ^ *} \）计算为：

其中\（z \）是随机高斯输入，Deconv（⋅）是任何折耦合运算符（如pytorch中的nn.convtransose2d）。我们还假设：

以上，我们调用\（Deconv_ {输出} \）（⋅）输出折块层。它们负责代表不同分辨率的“边缘颜色功能”（参见图3）。

换句话说，目标网络\（g \）*的每个隐藏层\（S_L ^ * \）负责生成权重，以确定要用于“绘制”输出图像的“哪个边缘颜色功能”。较低级别的隐藏层\（S_L ^ * \）负责生成用于绘制下层分辨率图像的权重;以及负责绘制更高分辨率图像的更高级别的隐藏层。

结果，当使用GAN学习现实生活图像时，人们应该期望学习者发生器的更高隐藏层\（g \）来学习 - 通过隐藏的解卷积层的组成 - 如何将较低分辨率的功能组合产生更高的功能 - 通过超级分辨率进行研究。

现实生活图像也很敏锐：含义可以清楚地看到物体边界的“对比度”和图像中对象中的“颜色一致性”。在生成模型中，我们将图像清晰度属性到隐藏图层的分层稀疏编码属性。

为了看到这一点，让我们回顾该现场图像通常通过输出解卷积层中的“边缘颜色特征”的稀疏组合生成。例如（参见图4），当图像中的贴片与对象的边界相关联时，可以选择“边缘特征”以在该补丁中生成像素，而所有其他功能都不太可能出现;相反，当补丁处于对象的中间时，可以选择“颜色特征”以绘制这些像素，而所有其他功能都不太可能出现。

在数学上，我们通过假设每层L和每个补丁p来模拟这一点，将隐藏层\（s_l ^ * \）的限制限制为此补丁 - 由\（[s_l ^ *] _p \）表示 - 是稀疏的矢量。这意味着在每个补丁中只有几个通道是非零（尽管这些非零通道可以在不同的补丁下不同）。通过测量图5中的隐藏层激活的稀疏性，我们经验经验验证了这一假设。

在这项工作中，我们表明，图像的分布的两个结构特性，即要确保不同分辨率的图像的语义一致性，以及确保图像清晰度的分层稀疏编码，足以为GAN有效地学习此类分布。在数学上，我们在新论文中证明了以下定理。

定理（非正式）：对于每个ε＆gt; 0，对于前进超分辨率和分层稀疏编码属性的任何D维分布，我们可以使用D和1 /ε中的样本和时间复杂度多项式来学习此类分配。 ，只需使用梯度下降上升（GDA）培训GAN。

在这篇博客中，让我们识别GAN如何在没有潜入数学细节的情况下学习这个分布。我们考虑层展培训：首先将学习者生成器\（g \）的第一层列车（与输出解卷积）一起生成最低分辨率图像\（x_1 \），然后训练第二层\（g \）（与输出解卷层）一起生成\（x_2 \），第三层生成\（x_3 \），等等。我们将学习分成不同的阶段。

要学习输出解卷积图层（即，来自\（x_l \）= \（deconv_ {output} \）\（（s_l ^ *）\）的任何一层\（l \）），我们显示足够的生成器学习匹配发电机输出图像和目标分布的真实图像之间的时刻。这是从早期的理论工作中已知的稀疏编码模型产生的分布的特殊属性，例如Andkumar等人。

直观地，输出解卷积层可以写成线性运算符\（x = ay \），其中矩阵a的每列代表边缘颜色特征，y是稀疏向量，该稀疏向量确定用于油漆的哪个边缘颜色功能输出图像\（x \）。它在标准规律性条件下（例如几乎列正交的\（a \）和\（y \）的足够稀疏性），适用于任何整数c＆gt; 0，第c-tround songe \（\ mathbb {e} \）\（[x ^ {⊗c}]≈\）\（Σ_i{a_i ^ {⊗c}} \（\ mathbb {e [y {_i ^ c}] \）其中\（a_i \）是\（i \） - th列（a \）。发生这种情况时，匹配瞬间\（\ mathbb {e} [x ^ {⊗c}]有效地确定矩阵\（a \）达到列排列。

换句话说，为了学习输出折耦层，它足以确保GaN发生器与其输出图像和真实图像之间的瞬间匹配。在理论方面，我们表明Relu型鉴别器可以区分图像上的时刻之间的错配，因此通过梯度下降开始，可以有效地学习输出折码层。在经验方面，图6（另见上文）表明，GAN确实在训练阶段期间匹配的时刻匹配。

学习第一个隐藏层（即，来自\的解压缩运算符（（s_ {1 ^ *} \）= \（Relu（CofOnv（\）\（z）））\），我们表明它还足以匹配时刻。

实际上，第一隐藏层\（s {_1 ^ *} \）的每个坐标都可以写成\（[s {_1 ^ *}] _ i \）= \（Relu（α_i⋅g_i-β_i）\） \（g_i \）是标准高斯。鉴于\（s {_1 ^ *} \）的时刻即使只是任何常量顺序，这个唯一地确定每个\（i \）的\（α_i\）和\（β_i\），以及确定成对相关性⟨ \（g_i \），\（g_j \）⟩。换句话说，如果鉴别者可以从目标生成器\（g ^ * \）和来自学习者生成器的隐藏层\（s_1 \）的瞬间区分隐藏层\（s_1 ^ * \）的时刻（g \），然后，这有效地确定了第一折叠层DECONV（⋅）直至整体变换。与阶段（1）的主要区别是，与输出图像不同，鉴别器没有访问隐藏层\（S_1 ^ * \），不能直接实现此刻匹配过程。

幸运的是，使用稀疏的编码属性，阶段（1）告诉我们鉴别器可以学习输出折叠层（调用它们是“边缘颜色的特征”）到下降准确性，因此它可以使用它们来执行\（S_1）进行解码^ * \）来自真实图像\（x_1 \）。这需要第一层鉴别器使用（大约）与发电机的输出层相同的相同的边缘颜色特征，并且与在实践中发生的情况一致（见图7）。

将阶段（1）和（2）放在一起，发电机不仅可以学习输出折折叠层，还可以学习第一个隐藏的解卷积层，从而了解\（X_1 \）的分布，即“最粗磨”全局图像的结构。

对于任何其他隐藏层（即来自\的解卷积运算符（s {_l ^ *} \）= \（Relu（reconv（\）\（s_ {l-1} ^ *））\（l \） ≥2），由于它捕获了图像的越来越尖锐的细节，因此不再知道矩的方法是足够的。

在这种情况下，我们示出了鉴别者学会鉴别真实图像和\（g \）输出图像之间的对（（（（x_ {l-1}，x_l））\）的统计差异。例如，鉴别器可以区分“\（X_2 \”始终成为\（X_3 \）的眼睛的情况。当这是这样的时候，发电机可以了解图像\（X_ {L-1} \）如何将超级分辨率执行到\（X_L \），每个\（L \）≥2的层。

前向超分辨率的学习过程应让人想起监督学习：目标是学习一个隐藏层神经网络，其作为输入下分辨率图像并输出更高分辨率的地图。注意从监督学习的一个主要区别在于，在\（s {_l ^ *} \）= \（reconv（\）\（s_ {l-1} ^ *））中，\），输入\（ s_ {l-1} ^ * \）和输出\（s {_l ^ *}）是隐藏的特征，而不是低分辨线和高分辨率图像\（x_ {l-1} \），\（x_l \）。同样，由于稀疏编码属性和阶段（1），我们表明鉴别器可以从其相应的图像\（X_ {L-1} \），\（X_L \）中解码这些隐藏特征。这允许GANS模拟监督学习，并了解如何将较低级别的功能合并以有效地产生更高级别的功能，纯粹地使用梯度下降升级。

GAN可以有效地学习这些超分辨率操作的另一个关键原因是此类操作非常本地：在图像的斑点上执行超分辨率，发电机仅需要查看附近的补丁而不是整个图像。实际上，全球结构已经在下层分辨率层中得到了处理。换句话说，学习每个隐藏层可以基本上修补而不是整个图像，如下图9所示。

在我们的工作中，我们还开展了一个实验，表明从下层分辨率图像中学到的特征确实非常有助于学习更高分辨率的图像。在图10中，我们考虑了甘甘的层面训练，我们首先首先训练发电机的第一个隐藏层，然后冻结它并仅训练发电机的第二层，等等。显然可以看到从较低分辨率图像中学到的特征确实可以用于在更高的分辨率下产生非常非琐碎的现实图像。我们相信这是强有力的证据表明，前瞻性超决议性的财产使GAN培训容易掌握现实生活的分布，尽管有最糟糕的硬度界限。

我们指出，我们的作品仍然初步，远远捕获了全部的GAN的全貌。最值得注意的是，我们专注于证明我们主要定理的“可实现的”设置。因此，从理论上的角度来看，它足以执行层次的学习：即，首先学习分布\（X_1 \）和隐藏的层\（S_1 ^ * \），然后学习分发\（X_2 \）和隐藏层\（ s_2 ^ * \），等等。

正如我们在图10所示，层面前进超分辨率已经比从随机较低级别的特征的学习更好地执行。但是，在实践中，我们可能会考虑更具挑战性的“不可知论”设置，其中图像的目标分布是错误的。如果我们在层展培训期间无法充分学习隐藏层，则此错误将传播到更深层层，如果我们执行层次学习，可能会爆炸。这是可以生成简单的图像，请参见图10.对于更复杂的图像，我们预计发电机网络通过完全训练更高级别的层，可以将发电机网络减少到较低级别的层上的这种误差。换句话说，当训练所有层次时，我们预期较低级别的层能够捕获更高的分辨率细节（而不是仅仅学习下部分辨率图像）。这种现象称为后向功能校正（BFC），其配备有监督深度学习的可证明的保证。扩展BFC的范围到GANS是一个重要的下一步。