希尔伯特大酒店的悖论

跳转到导航跳转以搜索Hilbert＆＃39; Grand Hotel的悖论（口语：无限Hotel Paradox或Hilbert＆＃39; S Hotel）是一个思想实验，说明了无限套装的反向性。它被证明，拥有无限的房间的完全占用的酒店仍然可以容纳额外的客人，甚至无限的客人，这一过程可能会不确定重复。这一想法是由大卫希尔伯特在1924年的讲座＆＃34;überdasunendliche＆＃34;，转载于（希尔伯特2013，第730页），并通过乔治·格洛＆＃39;第1947页推荐一两三个。 。 无限。 [1] [2]

考虑一个假设的酒店，拥有一个可占用的无限数量的房间，所有这些都是占用的。可能会想到酒店无法容纳任何新抵达的客人，就像有限数量的房间一样，鸽舍原则将适用。

假设新客人到达并希望在酒店享受。我们可以（同时）将嘉宾当前在1到房间2到2房间，当前在2到2间到3室，依此类推，将每位客人从他们当前的房间N + 1移动。在此之后，房间1是空的，新客人可以进入该房间。通过重复此程序，可以为任何有限数量的新客人腾出空间。一般来说，假设k客人寻找一个房间。我们可以应用相同的程序，并将每个客人从N + k室内移动。以类似的方式，如果嘉宾希望离开酒店，则每位客人都从N到房间移动到N - K。

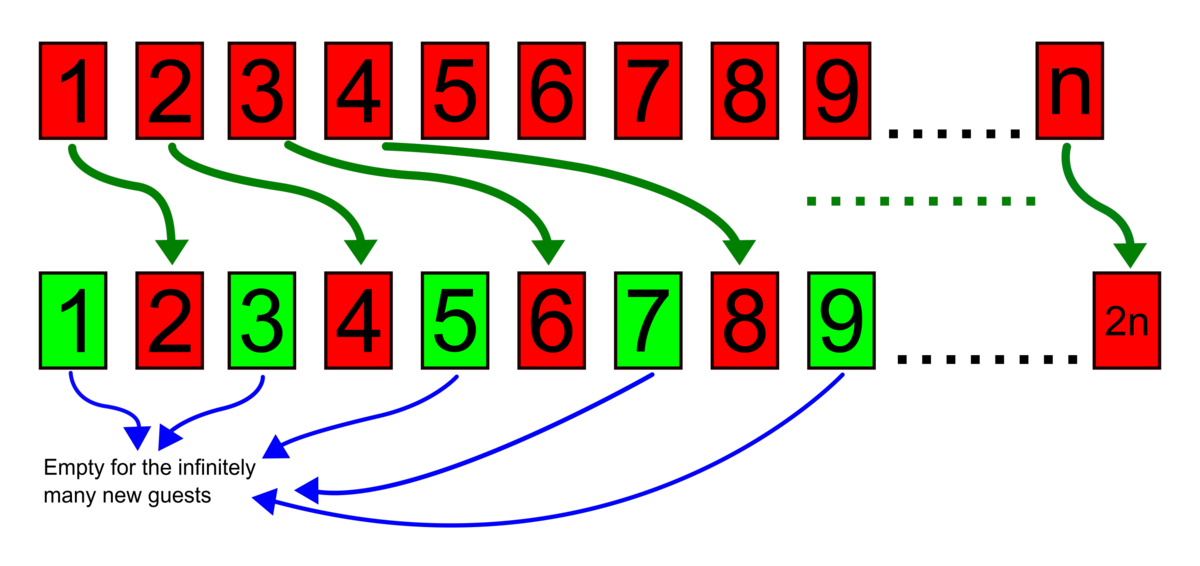
也可以适应一个可爱的无限新的嘉宾：只需将占据房间1到2房间的人员2到4房间，占据4室，而且，一般来说，客人占据房间N到2 N（2时间n），所有奇数的房间（可数无限的房间）将免费为新客人免费。

通过几种不同的方法，可以通过几种不同的方法适应各种无限乘客的无限多重的一支乘客。大多数方法都依赖于已经编号的教练中的座位（或使用可数选择的公理）。通常，任何配对功能都可用于解决这个问题。对于每种方法，考虑乘客＆＃39;在COACH上的座位号，以n {\ displaystyle n}，他们的coach编号是c {\ displaystyle c}，以及数字n {\ displaystyle n}和然后将C {\ DisplayStyle C}馈入配对功能的两个参数。

通过将客人送到房间里的房间我{\ displaystyle i}来清空奇数的房间。然后将第一个教练＆＃39;在房间3 n {\ displaystyle 3 ^ {n}}，第二个教练＆＃39;房间的负载5 n {\ displaystyle 5 ^ {n}};对于Coach Number C {\ DisplayStyle C}我们使用的房间P n {\ displaystyle p ^ {n}}其中p {\ displaystyle p}是c {\ displaystyle c} th奇数素数。该解决方案将某些房间留下（可能或可能对酒店有用）;具体而言，不再占用，例如15或847，这不是序号的所有奇数。 （所以，严格来说，这表明抵达的数量小于或等于所创建的空缺数量。通过独立的方式更容易地显示到达数量也大于或等于数字。空缺，因此它们是相等的，而是比将算法修改为精确的拟合。它必须均匀应用。）

您可以将某个座位的{\ displaystyle s}和coach c {\ displaystyle c}的每个人放入2 s 3 c {\ displaystyle 2 ^ {s} 3 ^ {c}}（假定c = 0人们已经在酒店，1个为第一个教练等......）。因为每个数字都有一个独特的素数分解，它易于看待所有人都有一个房间，而没有两个人将在同一个房间里。例如，2592室中的人（2 5 3 4 {\ DisplayStyle 2 ^ {5} 3 ^ {4}}）在第4位教练上坐在第五位。像Prime Powers方法一样，这个解决方案将某些房间留下。

这种方法也可以很容易地扩展无限夜晚，无限入口等......（2 s 3 c 5 n 7 e {\ displaystyle 2 ^ {s} 3 ^ {c} 5 ^ {n} 7 ^ {e }}）

对于每个乘客，将N {\ DisplayStyle n}和c {\ displaystyle c}的长度进行比较，如在任何位置数字系统中写入，例如十进制。 （将每家酒店居住在教练＃0中。）如果任一数字较短，则将前导零添加到它，直到两个值都具有相同数量的数字。交织数字以产生房间号：其位数将是[Coach编号的第一位] - [座位号的第一位数] - [Coach编号的第二位数] - [座位号的第二位数] - etc。酒店（Coach＃0）客人在房间1729年搬到01070209（即1,070,209室）。 Coach 789的座椅1234上的乘客进入01728394（即，1,728,394室）。

与主要权力解决方案不同，这一点完全填补了酒店，我们可以通过逆转交织过程来重建嘉宾和座位。首先，如果房间有奇数的数字，则添加前导零。然后将该号码解交换为两个数字：Coach编号由奇数数字组成，座位号是偶数编号的数字。当然，原始编码是任意的，并且两个数字的角色可以颠倒（座椅奇数和教练 - 偶数），只要它始终应用。

已经在酒店中的人将被移动到房间（n 2 + n）/ 2 {\ displaystyle（n ^ {2} + n）/ 2}，或n {\ displaystyle n} th三角编号。教练中的那些将在室内（（C + N - 1）2 + C + N - 1）/ 2 + N {\ DisplayStyle（（C + N-1）^ {2} + C + N-1） / 2 + n}，或（c + n - 1）{\ displaystyle（c + n-1）}三角数加n {displaystyle n}。通过这种方式，所有房间都将被一个人填充，只有一个，客人。

可以通过将酒店视为一室深，无限的金字塔来视觉上展示该配对功能。金字塔＆＃39;最顶级的排是单一房间：1房间;它的第二行是房间2和3;等等。由最右边的房间组成的柱将对应于三角形数字。一旦他们填补（由酒店＆＃39;重新分配乘客），剩下的空房间就形成了金字塔的形状与原始形状完全相同。因此，可以针对每个无限集重复该过程。每次为每个教练做这一点需要一个无限的步骤，而是通过使用先前的公式，客人可以确定他的房间和＃34;将是＆＃34;一旦他的教练达到了这个过程，就可以立即去那里。

让s：= {（a，b）| a，b = n} {\ displaystyle s：= \ {（a，b）\ mid a，b \ in \ mathbb {n}}。 S {\ DisplayStyle S}是可计算的，因为n {\ displaystyle \ mathbb {n}}可计算，因此我们可以枚举其元素s 1，s 2，... {\ displaystyle s_ {1}，s_ {2}，\ dots }。现在，如果sn =（a，b）{\ displaystyle s_ {n} =（a，b）}，则为n {\ displaystyle a} th coach分配b {\ displaystyle b} the the n {\ displaystyle N} Th Room（考虑在酒店的客人作为0 {\ DisplayStyle 0} Th Coach的客人。因此，我们有一个将每个人分配给房间的职能;此外，此任务不会跳过任何房间。

假设酒店毗邻海洋，每次携带无限数量的教练，每次乘客都有无限数量的乘客。这是一个涉及三个＆＃34;水平＆＃34;无限，它可以通过以前任何解决方案的扩展来解决。

可以通过为每个附加的无穷大添加新的素数（2 s 3 c 5 f {\ displaystyle 2 ^ {s} 3 ^ {s} 3 ^ {c} 5 ^ {f}}来应用所述序列分解方法。使用f {\ DirmanyStyle F}渡轮）。

可以使用素数的进一步指数应用主要功率解决方案，从而导致非常大的房间数，甚至给予小输入。例如，第二次渡轮上的第三母线的第二位（地址2-3-2）的第二个座位中的乘客将提高第二个奇数（5）至49，这是第三奇素（7）的结果提升到座位号的力量（2）。这个房间数量有超过三十个十进制数字。

交织方法可以与三个交错的＆＃34一起使用;股线＆＃34;而不是两个。带有地址2-3-2的乘客将转到232室，而具有地址4935-198-82217的乘客将转到房间＃008,402,912,391,587（即可移除前导零）。

酒店预计任何数量的无限客人的可能性，酒店可能希望分配房间，以便任何客人都需要移动，无论以后多少客人都到达。一个解决方案是将每个到达＆＃39; s地址转换为二进制数，其中一个解决方案在每个层的开始时用作分隔符，而给定层内的数字（例如客人＆＃39; s coach编号）是用那个零点代表。因此，具有先前地址2-5-1-3-1（五个无限层）的客人将转到10010000010100010（十进制295458）。

作为在该过程中的添加步骤中，可以从数字的每个部分中删除一个零;在这个例子中，嘉宾＆＃39;新房间是101000011001（十进制2585）。这确保了每个房间都可以被一个假设的客人填充。如果没有无限的客人到达，那么只有两个电源的房间将被占用。

虽然可以找到房间的人的任何有限数量的人，但对于无限数量的层，也不总是如此，即使在每层都存在有限数量的元素。

希尔伯特＆＃39;悖论是一个明显的悖论：它导致一个逆向直观的结果，这些结果被证明是真实的。该陈述＆＃34;每个房间都有客人＆＃34;和＃34;没有更多的客人可以容纳＆＃34;当没有无限的房间时，不等同。

最初，这种状况似乎可能是反直观的。 ＆＃34的属性;无限的东西＆＃34;与那些＆＃34有很大不同;有限的东西＆＃34;利伯特＆＃39的悖论可以通过使用Cantor＆＃39; Transfinite数字理论来理解。因此，在一个拥有多个房间的普通（有限的）酒店，奇数房间数量明显小于房间总数。但是，在希尔伯特＆＃39;恰当地命名为Grand Hotel，奇数房间的数量不小于总＆＃34;数字＆＃34;房间。在数学术语中，包含奇数房间的子集的基数与所有房间集的基数相同。实际上，无限集表征为具有相同基数的适当子集的集合。对于可数集（与自然数相同的基数设置）这种基数是ℵ0{\ displaystyle \ aleph _ {0}}。 [3]

对于任何可选的无限集，还存在一个映射到一组自然数的映射函数，即使可选的无限集包含自然数。例如，可以写入作为整数的商写入的那些数字的集合 - 包含作为子集的自然数，但是由于基于Rationals是可计算的，因此没有比自然数量的一组更大：有一个击倒基于理性的自然。

BBC学习区反复筛选1996年的一九九六届一次性教育Docudrama Hotel Hilbert在酒店中坐落在一位年轻女性宾馆骑士的眼睛看，她的名字是有限的双关语。该计划旨在教育观众关于无限的概念。 [4]

Mathematician /科幻作家Rudy Rucker的新型白光包括基于希尔伯特＆＃39;悖论的酒店，故事的主角符合Georg Cantor。

斯蒂芬巴克斯特＆＃39;科学小说小说超越于关于无限的本质，并基于悖论的解释，修改为使用星舰士兵而不是酒店。

Geoffrey A. Landis＆＃39;星云屡获殊荣的短篇小说＆＃34;狄拉科＆＃34的涟漪;使用Hilbert Hotel作为为什么无限完整的Dirac Sea仍然可以接受粒子的解释。

在PeterHøeg＆＃39;小小的小姐Smilla＆＃39; Smilla＆＃39的感觉，这个名为Heroine反映了酒店＆＃39; S Manager和客人可以去所有麻烦，以便拉脱莫尔可以拥有自己的困难房间和一些隐私。

在ivar ekeland＆＃39;小说儿童，猫在数兰，A＆＃34;先生。希尔伯特＆＃34;他的妻子为所有整数运行了一个无限的酒店。故事通过三角法的理性方法进行了进展。

在Will Wiles＆＃39;小说Way Inn，关于一个无限的大型汽车旅馆，恶棍＆＃39;姓名是Hilbert。

在Reginald Hill＆＃39; s小说和＃34;陌生人房子＆＃34;角色山姆是指帕拉德帕拉德酒店。

Naum Ya的短篇小说。 Vilenkin The Offerorvinary Hotel（经常被错误地归功于Stanislaw LEM）显示了Hilbert＆＃39; S Grand Hotel在无限新的主机到达时可以重新装饰的方式。

John Roderick和Ken Jennings在Hilbert Hotel Entry中展在了他们的综合播客中的酒店。

漫画书Saga由Alan Moore和Kevin O＆＃39的非凡绅士系列联盟的暴风雨;内尔显示一个名为无限远的恶棍。在故事中，有人建议小人基于希尔伯特＆＃39;悖论进入酒店。 Georg Cantor也被提及。

^ gamow，乔治（1947）。一两个三...无限：科学的事实和猜测。纽约：Viking Press。 p。 17。

^ Rucker，Rudy（1984）[1982]。 无限和心灵。 无限的科学与哲学。 圣骑士。 第73-78页。 ISBN 0-586-08465-7。 希尔伯特，大卫（2013），埃沃德，威廉; Sieg，Wilfried（EDS。），David Hilbert＆＃39;讲座的算术和逻辑基础1917-1933，海德堡：Springer-Verlag，Doi：10.1007 / 978-3-540-69444-1，ISBN 978-3 -540-20578-4 Nancy Casey，欢迎来到酒店无限！ - 悖论被称为一个幽默的叙述，包括一家酒店所有者和基于令人震惊的19世纪数学家Georg Cantor和Leopold Kronecker的建筑承包商 在p上看到歌曲。 2006年10月704日美国数学月度或p。 2011年12月177日数学和艺术杂志