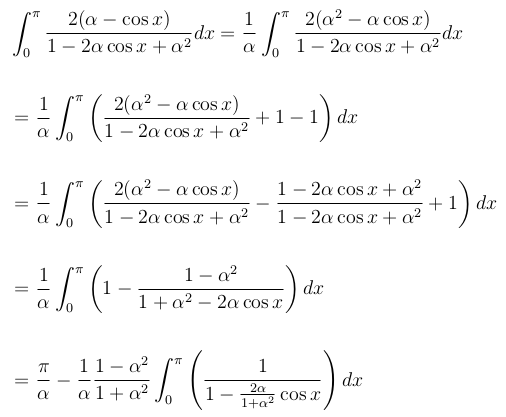Richard Feynman的组成技巧

“我学会通过在一本书中显示的各种方法来做积分，即我的高中物理老师獾先生给了我。 [它]显示如何在整体符号下区分参数 - 这是一定的操作。事实证明，大学没有在大学教授;他们不强调它。但是我抓住了如何使用该方法，我再次使用那个该死的工具。 [如果是麻省理工学院或普林斯顿的人有一定的积分，[那么]我来了，尝试在整体标志下区分，并且经常工作。所以我在做积分的声誉很大，只有因为我的一盒工具与其他人不同，他们在给我的问题之前尝试了所有的工具。“ （当然，你笑着，Feynman先生！）

今天的文章将讨论一个模糊但强大的集成技术，最俗称在整体标志下的差异化，但由于他在他的书中推广了这种技术而被称为“Feynman的技术”，并且被称为Leibniz积分规则。

在我们开始之前澄清的一点：虽然Leibniz规则有时被称为“Feynman的技术”或类似的名称，但它不与Feynman的路径积分制定量子力学。因此，在本文的其余部分，我将通过正确的名称引用它。

Feynman提到上述报价的书是先进的Conculus于1926年发表了一个名为Frederick Soods的麻省理工学院的Mit Mathematician，这一整数来自那本书，并在Wolfram Mathworld上传了。

您可以尝试使用微积分中学的常用技术。 Trig替换，变化变化，零件集成，用一系列替换积分，否则都没有工作。您也可以尝试使用wolfram alpha计算它，它将超时。我们需要更具创意。

首先，您应该首先观察到相对于积分的任意常数。由于确定的积分将是依赖于alpha的数字，因此我们可以将这种积分视为alpha的函数。该方法的轮廓如下：

计算alpha某些特定方便值的积分。在这种情况下，如果alpha等于一个，那么积分等于零，这给了我们条件f（1）= 0.我们将需要这一步。

使用f（1）= 0计算集成常量值的事实。

我们所做的是，我们已经改变了计算整体求解一个简单的微分方程的问题。观察：

似乎我们只让自己更加糟糕了。底线末端的积分看起来特别强大，但它可以用一点代数巧妙计算。

这个最后一个积分比它看起来更简单。我们必须摆脱余弦功能。为此，我们可以做一个“反向”U替代。

注意：因为| alpha |大于或等于1，u为正或零，y从零到负无穷大。所以：

通过集成和使用F（1）= 0，我们可以完成积分的计算：

在第一个示例中，我们与已区分的参数已经存在于Integrand中。但是，整数标志下的差异的真正力量是我们也可以将参数自由地将参数插入到集成状态中，以便使其更具易行。从2005年威廉洛尔·普特南数学竞赛中考虑以下内容。

对于那些不知道的人来说，Putnam竞赛是在12月每年为数学专业提供的问题解决比赛。它的声誉对于强烈困难，平均得分通常在120中介于0到1之间。该测试以两组六个问题交付，A5和A6通常在第一组中最困难。所以这种积分应该是非常困难的，尽管它巧妙地驯服了外观（顺便说一下，这是一个技巧：测试是值限的，所以这是一个陷阱，让你浪费时间尝试计算与基本微积分技术的积分计算成分，这将不起作用）。但是，通过仔细介绍参数并使用我们开发的技术，可以使这种积分变得非常简单。

请注意，这意味着我们的原始积分是i（1）并且i（0）= 0.让我们现在继续如之前继续：

通过部分分数分解获得第二线。这些是可以立即计算的基本积分以获得第三行。由于我（0）= 0，通过微积分的基本定理：

请注意，我们也可以如在第一个示例中，以求解A的差分方程，然后使用I（0）= 0条件来确定在插入A = 1之前确定特定的解决方案I（A）。使用FTC在这里做同样的事情，但短圈几步。

这是一个基本积分，可以通过标准技术一次计算。结果是：

这是2005年考试解决方案中积分的价值。请注意，解决方案表讨论了其他方法接近这种积分，但这种方式是最简单，最优雅的，更不用说最快。

数学问题解决中最重要的技能之一是概括的能力。给定的问题，例如我们刚刚计算的积分，可能似乎是独立的。然而，通过踩回并考虑不孤立的问题，而是作为一整类相关问题的个别成员，我们可以辨别以前隐藏的事实。尝试计算特定值A = 1的积分太困难，所以我们计算了每种可能值的积分的值。矛盾的是，有很多情况，实际上更容易解决一个普遍的问题，而不是解决特定的问题。

我也认为这强调了愿意在课堂外学习的重要性。 通常在数学和科学课程中，时间限制和其他因素意味着有时教育者别无选择，只能在课程中包含某些科目。 这意味着，如果您没有主动指导自己的学习，那么您将错过的很多潜在的非常有趣和有用的知识。 如果您有任何主题，您可以了解更多信息，请随时在评论中告知我。 本文是一系列关于数学相关主题的一系列故事的一部分，在Cantor的天堂，每周中等出版物。 谢谢你的阅读！